LiNbO3和LiTaO3晶体电子结构、平面声波和光折射特性

doi:10.15541/jim20150338

摘要/Abstract

摘要：

本研究基于密度泛函理论的第一性原理超软赝势平面方法计算了LiNbO₃和LiTaO₃的晶格参数、电子结构和弹性常数, 并利用Christoffel方程研究了二者平面声波特征。结果表明: 两者的理论计算晶格参数和弹性常数与实验值接近, 禁带宽度分别为3.78和3.98 eV, 导带底和价带顶主要由O-2p和Nb-4d(Ta-5d)态电子贡献。化学键理论揭示Li和Nb(Ta)与O原子之间有两种成键类型。电荷布局分析结果显示有两种相应的重叠布居数, Nb(Ta)-O键呈现强共价键作用, 并且Nb-O(Ta-O)键长小于Li-O键长。LiNbO₃和LiTaO₃晶体平面声波有两支横波和一支纵波, 纵波速度大于横波速度, 在xy平面呈现六重对称性, 在xz和yz平面各向异性程度强于xy平面, 沿[001]、晶向上两支横波振动速度相等。最后利用模守恒赝势(Norm-conserving)计算了介电常数和静态折射率, 计算表明LiNbO₃晶体的折射性能和非寻常光(e光)离散程度均强于LiTaO₃晶体。

关键词: 第一性原理, 电子结构, 弹性常数, 平面声波, LiNbO3, LiTaO3

Abstract:

Lattice parameters, electronic structures and elastic constants of lithium niobate and lithium tantalate were calculated with the plane wave pseudopotential method based on the first-principles density functional theory. The results show that calculated lattice parameters and elastic constants are in consistent with the corresponding experimental values. It was found that the bottom of the valence band and the top of the conductive band are mainly determined by electron orbits of O-2p and Nb-4d (Ta-5d). The chemical bonds theory indicate that Li, Nb (Ta) and O atoms have two types of bonds, and the Mulliken population analysis exhibits that there are two corresponding bond populations. The Nb-O (Ta-O) covalence is stronger than that of Li-O, and band length shorter than that of Li-O. Moreover, the planar acoustic velocities, studied by Christoffel equation, shows that the three-dimensional images of the planar acoustic wave consisting of a longitudinal wave and two transverse waves, indicating the anisotropic feature. The velocity of the longitudinal wave is larger than those of the two transverse waves. In xz and yz planes, not only the plane projections of the planar acoustic waves show the stronger anisotropy than those in xy plane which have a six-fold symmetry, but also the velocities of the two transverse waves are equal in [001] and directions. The calculated static dielectric constants and optical permittivity indicate the refractive index of LiNbO₃is stronger than that of LiTaO₃.

Key words: first-principles, electronic structure, elastic constants, planar acoustic velocity

中图分类号:

O735

邵栋元, 程南璞, 陈晶晶, 李孝, 陈志谦, 李春梅, 惠群. LiNbO₃和LiTaO₃晶体电子结构、平面声波和光折射特性[J]. 无机材料学报, 2016, 31(2): 171-179.

SHAO Dong-Yuan, CHENG Nan-Pu, CHEN Jing-Jing, LI Xiao, CHEN Zhi-Qian, LI Chun-Mei, HUI Qun. Electronic Structure, Plane Acoustic Velocity and Refractive Property of LiNbO₃and LiTaO₃[J]. Journal of Inorganic Materials, 2016, 31(2): 171-179.

图/表 13

图1 LiNbO3、LiTaO3晶体结构

Fig. 1 The crystal structure of LiNbO3 or LiTaO3

表1 晶格参数(a, c)、密度ρ和体积V

Table 1 Lattice constants (a, c), density ρ and volume V

Material	Method	(a=b)/nm	c/nm	ρ/(g·cm^-3)	V/nm³
LiNbO₃	Exp	0.51483	1.3863		0.131821^[24]
	LDA	0.52332	1.4131	4.395	0.33514
	GGA	0.52447	1.4222	4.251	0.33999
	PBEsol	0.51531	1.3837	4.630	0.31821^[7]
LiTaO₃	Exp	0.5147	1.3766		0.31585^[24]
	GGA	0.5104	1.3546	7.434	0.32610
	LDA	5.050	13.386	7.433	0.29578
	LDA	5.129	13.938	7.400	0.31763^[7]

图2 LiNbO3和LiTaO3晶体分波态密度

Fig. 2 Partial density of states of LiNbO3 and LiTaO3

图3 LiNbO3(a)和LiTaO3(b)能带结构

Fig. 3 Energy band structures of LiNbO3(a) and LiTaO3(b)

图4 LiNbO3和LiTaO3 和电荷密度

Fig. 4 The contour charge densities of LiNbO3 and LiTaO3 in and planes

表2 LiNbO3和LiTaO3原子轨道电子占据数、各原子静电荷、键长(L1, L2)和电子云重叠布居(P1, P2)

Table 2 Atomic orbital populations, atomic charges, bond lengths (L1, L2), and band populations (P1, P2) of LiNbO3 and LiTaO3

Material	Atom	s	p	d	Total	Charge	Bond	L₁/nm	P₁	L₂/nm	P₂
LiNbO₃	Li	-0.17	0	0	-0.17	1.17	O—Nb	0.1971	0.79	0.2184	0.37
	O	1.87	4.87	0	6.75	-0.75	O—Li	0.2084	-0.06	0.2289	0.01
	Nb	0.36	0.38	3.20	3.93	1.07	O—O	0.2869
LiTaO₃	Li	0.22	0	0	-0.22	1.22	O—Ta	0.1852	0.82	0.2047	0.45
	O	1.84	4.99	0	6.83	-0.83	O—Li	0.2093	-0.08	0.2230	0.01
	Ta	0.38	0.41	2.94	3.73	1.27	O—O	0.2669

表3 LiNbO3和LiTaO3晶体弹性常数Cij

Table 3 Elastic constants Cij of LiNbO3 and LiTaO3

Material	Method	C₁₁/GPa	C₁₂/GPa	C₁₃/GPa	C₁₄/GPa	C₃₃/GPa	C₄₄/GPa	C₆₆/GPa
LiNbO₃	LDA	191.7	61.8	71.7	4.6	205.1	57.7	64.9
	GGA	160.11	9.37	19.36	-12.04	161.77	63.50	75.37
	Other work	203.0	53.0	75.0	9	245.0	60	75^[4]
	Other work	196.9	54.8	66.4	0	225.4	58.8^[7]
LiTaO₃	GGA	193.6	44.1	58.9	21.7	292.1	39.3	74.7
	LDA	235.7	64.1	97.6	11.6	256.1	60.7	85.8
	Other work	233.3	47.0	80.0	-11.0	275.0	94.0^[4]
	Other work	235.2	63.8	87.7	0	264.1	102.1^[7]

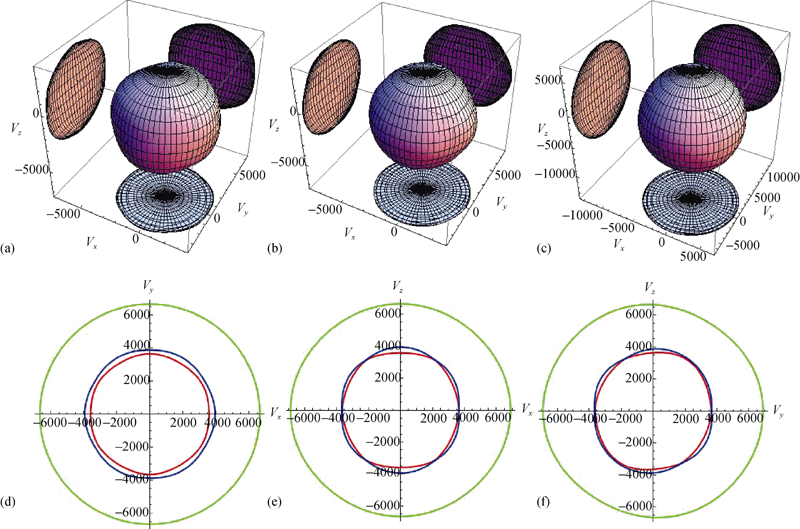
图5 LiNbO3晶体平面声波三维图(a, b横波模型, c纵波模型)与平面投影图(d~f) (红线和蓝线表示横波, 绿线表示纵波)(LDA)

Fig. 5 The 3-D planar acoustic velocities, in which a and b are transverse wave models, and c longitudinal model, and the plane projected pictures of LiNbO3 with red and blue lines indicating transverse wave velocities, and the green line indicating longitudinal wave velocity (LDA)

图6 LiTaO3晶体平面声波三维图(a, b横波模型, c纵波模型)与平面投影图(d~f) (红线和蓝线表示横波, 绿线表示纵波) (LDA)

Fig. 6 The 3-D plane acoustic velocities, in which a and b are transverse wave models, and c longitudinal model, and the planar projected picture of LiTaO3 crystal with red and blue lines indicating transverse wave velocities, and the green line indicating longitudinal wave velocity (LDA)

表4 不同晶向平面声波速度v1, v2, v3

Table 4 The planar acoustic velocities v1, v2, v3 in different crystal orientations

表5 静态介电常数ε (0)、静态折射率n和光学介电常数ε(∞)

Table 5 Calculated static dielectric constants ε (0), static refractive indices n and optical permittivity ε (∞)

Materal	Method	Index	ε(0)	n	ε(∞)
LiNbO₃	GGA	11	43.6779	2.5401	6.4557
	GGA	33	30.6094	2.4925	6.2126
	LDA	11	43.6779	2.5587	6.5467
	LDA	33	30.6094	2.5408	6.4980
	Other Work^[7]	11	50.42	2.58	6.68
		33	34.16	2.57	6.58
		11	41.50	2.29	5.00
		33	26.00	2.20	4.60
LiTaO₃	GGA	11	47.0227	2.1751	4.7311
	GGA	33	31.9626	2.2199	4.8637
	LDA	11	34.1709	2.2054	4.9278
	LDA	33	34.8047	2.2236	4.9446

图7 折射率no和ne随入射角的变化

Fig. 7 Incidence angle-dependent refractive index no and ne of LiNbO3 (a) and LiTaO3 (b)

图8 LiNbO3和LiTaO3晶体非寻常光离散角

Fig. 8 The discrete angles of extraordinary wave for LiNbO3 and LiTaO3 crystals

参考文献 35

[1]	CHEN WEI-JUN, LU KE-QING, HUI JUAN-LI, et al.Study onnonlinear surface waves along the boundary of LiNbO3 crystals.Acta Physica Sinica, 2015, 64(1): 014204.
[2]	BUSACCA A C, STIVALA S, CURCIO L, et al.Soft protonxchanged channel waveguides in congruent lithium tantalite for frequency doubling.Optics Express, 2010, 18(25): 25967-25972.
[3]	KUSHIBIKI J, TAKANAGA I, ARAKAWA M, et al.Accurate measurements of the acoustical physical constants of LiNbO3 and LiTaO3 single crystals.IEEE Transactions on Ultrasonics ferroelectrics and Frequency Control, 1999, 46(5): 1315-1323.
[4]	ABD-ALLA A N, ASKAR N A. Calculation of bulk acoustic wave propagation velocities in trigonal piezoelectric smart materials.Applied Mathematics & Information Sciences, 2014, 8(4): 1625-1632.
[5]	LIU MEI-NAN, XUE DONG-FENG, LI KE-YAN.Soft-chemistry synthesis of LiNbO3 crystallites. Journal of Alloys and Compounds, 2008, 449(1): 28-31.
[6]	GONG XIN-XIN, FANG MING, FEI GUAN-TAO, et al.LiTaO3 microbubes: thelayered structure and the increased Curie temperature. Royal Society of Chemistry, 2015, 5: 31615-31621.
[7]	YANG JIN, LONG JIAN-PING, YANG LI-JUN.First-principles investigations of the physical properties of lithium niobate and lithium tantalite.Physica B, 2013, 425(12): 12-16.
[8]	TOYOURA K, OHTA M, NAKAMURA A, et al.First-principles study on phase transition and ferroelectricity in lithium niobate and tantalate. Journal of Applied Physics, 2015, 118(6): 64103.
[9]	LI JIN, ZHOU XIAN-MING, ZHU WEN-JIN, et al.Ashock- induced phase transformation in a LiTaO3 crystal.Journal of Applied Physics, 2007, 102(8): 083503.
[10]	SANG DAN-DAN, WANG QING-LIN, HAN CHONG, et al.Electronic and optical properties of lithium niobate under high pressure: A first-principles study. Chinese Physics B, 2015, 24(7): 077104.
[11]	LIU YUE, ZHU HAO-NAN, PEI ZI-DONG, et al.Molecular dynamic simulations of surface morphology and pulsed laser deposition growth of lithium niobate thin films on silicon substrate.Chinese Physics B, 2015, 24(5):056802.
[12]	NAKAMURA K, HIGUCHI S, OHNUMA T.First-principles in vestigation of pressure-induced phase transition in LiNbO3.Journal of Applied Physics, 2012, 111(3):033522.
[13]	MUKAIDE T, YAGI T, MIYAJIMA N, et al.High pressure and high temperature phase transformations in LiNbO3. Journal of Applied Physics, 2003, 93(7): 3852-3858.
[14]	WANG FAN-HOU, YANG JUN-SHENG, HUANG DUO-HUI, et al.Study on magnetic and optical properties of Mn-deped LiNbO3 by using the first principles.Acta Physica Sinica, 2015, 64(9): 097102.
[15]	REICHENBACH P, KAMPFE T, THIESSEN A, et al.Multiphton photoluminescence contrast in switched Mg: LiNbO3 and Mg:LiTaO3 single crystals.Applied Physics Letters, 2014, 105(12): 122906.
[16]	ZHAO BAI-QIANG, ZHANG YUN, QIU XIAO-YAN, et al.First-principles study of the electronic structures and absorptionspectrum of Fe: Mg: LiNbO3 crystals.Acta Physica Sinica, 2015, 64(12): 124210.
[17]	MAMOUN S, MERAD A E, GUILBERT L.Energy band gap and optical properties of lithium niobate from ab initio calculations.Computational Materials Science, 2013, 79: 125-131.
[18]	SHAO DONG-YUAN, CHENG NAN-PU, CHEN ZHI-QIAN, et al.First-principles studies electronic structures and optical properties of LiNbO3 under high pressure.Journal of Atomic and Molecular Physics, 2014, 31(6): 6-13.
[19]	RIMEIKA R, SEREIKA A, ČIPLYS D.Acoustoelectric effects in reflection of leaky acoustic waves from LiTaO3 crystal surface coated with metal film.Applied Physics Letters, 2011, 98(5): 052909.
[20]	ANISIMKIN V I.Anisotropy of the acoustic plate modes in ST-Quartz and 128 degrees Y-LiNbO3.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2014, 61(1): 120-132.
[21]	ALSHITS V I, LOTHE J.Acoustic axes in trigonal crystals.Wave Motion, 2006, 43(3): 177-192.
[22]	ČIPLYS D, RIMEIKA R.Measurements of electromechanical coupling coefficient for surface acoustic waves in proton exchanged lithium niobate.Ultragarsas, 1999, 3(33): 14-20.
[23]	TAKANAGA I, KUSHIBIKI J.A method of determining acoustical physical constants for piezoelectric materials by line-focus-beam acoustic microscopy.IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2002, 49(7): 893-904.
[24]	OHGAKI M, TANAKA K, MARUMO F.Anharmonic thermal vibration in a crystal of lithium(I) tantalum(V) trioxide, LiTaO3.Mineralogical Journal, 1989, 14(8): 373-382.
[25]	HOHENBERG P, KOHN W.Inhomogeneous electron gas.Physical Review B, 1964, 136(3B): 864-871.
[26]	CEPERLEY D M, ALDER B J.Ground state of the electrongas by a stochastic method.Physical Review Letters, 1980, 45(7): 566-569.
[27]	PERDEW J P, BURKE K, ERNZERHOF M.Generalized gradient approximation made simple.Physical Review Letters, 1996, 77(18): 3865-3868.
[28]	VANDERBILT D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism.Physical Review B, 1990, 41(11): 7892-7895.
[29]	MONKHORST H J, PACK J D.Special points for Brillouin-zone integrations.Physical Review B, 1976, 13(12): 5188-5192.
[30]	BROYDEN C G.The convergence of a class of double-rank minimization algorithms 1. General Considerations.Ima Journal of Applied Mathematics, 1970, 6(1): 76-90.
[31]	FLETCHER R.A new approach to variable metric algorithms.Computer Journal, 1970, 13(3): 317-322.
[32]	GOLDFARB D.A family of variable-metric methods derived by variational means.Mathematics of Computation, 1970, 24(109): 23-26.
[33]	SHANNO D F.Conditioning of quasi-newton methods for function minimization.Mathematics of Computation, 1970, 24(4): 647-656.
[34]	OZISIK H, COLAKOGLU K, OZISIK H B, et al.Structural, elastic, and lattice dynamical properties of Germanium diiodide (GeI2).Computational Materials Science, 2010, 50(2): 349-355.
[35]	陈纲, 廖理几. 晶体物理学基础. 北京: 科学出版社, 1992(2): 238-276.

LiNbO₃和LiTaO₃晶体电子结构、平面声波和光折射特性

Electronic Structure, Plane Acoustic Velocity and Refractive Property of LiNbO₃and LiTaO₃

RichHTML

PDF (PC)

可视化

被引次数

摘要/Abstract

引用本文

使用本文

图/表 13

参考文献 35

相关文章 15

编辑推荐

Metrics

本文评价

[1]	吴玉豪, 彭仁赐, 程春玉, 杨丽, 周益春. Hf_xTa_1-_xC体系力学性能及熔化曲线的第一性原理研究[J]. 无机材料学报, 2024, 39(7): 761-768.
[2]	靳宇翔, 宋二红, 朱永福. 3d过渡金属单原子掺杂石墨烯缺陷电催化还原CO₂的第一性原理研究[J]. 无机材料学报, 2024, 39(7): 845-852.
[3]	王伟华, 张磊宁, 丁峰, 代兵, 韩杰才, 朱嘉琦, 贾怡, 杨宇. 铱衬底上金刚石外延形核与生长: 第一性原理计算[J]. 无机材料学报, 2024, 39(4): 416-422.
[4]	张宇晨, 陆知遥, 赫晓东, 宋广平, 朱春城, 郑永挺, 柏跃磊. 硫族MAX相硼化物的物相稳定性和性能预测[J]. 无机材料学报, 2024, 39(2): 225-232.
[5]	陈梦杰, 王倩倩, 吴成铁, 黄健. 基于DFT的描述符预测生物陶瓷的降解性[J]. 无机材料学报, 2024, 39(10): 1175-1181.
[6]	周云凯, 刁亚琪, 王明磊, 张宴会, 王利民. 聚苯胺改性Ti₃C₂(OH)₂抗氧化性的第一性原理计算研究[J]. 无机材料学报, 2024, 39(10): 1151-1158.
[7]	吴晓维, 张涵, 曾彪, 明辰, 孙宜阳. 杂化泛函HSE和PBE0计算CsPbI₃缺陷性质的比较研究[J]. 无机材料学报, 2023, 38(9): 1110-1116.
[8]	张守超, 陈洪雨, 刘洪飞, 杨羽, 李欣, 刘德峰. 6H-SiC中子辐照肿胀高温回复及光学特性研究[J]. 无机材料学报, 2023, 38(6): 678-686.
[9]	杨颖康, 邵怡晴, 李柏良, 吕志伟, 王路路, 王亮君, 曹逊, 吴宇宁, 黄荣, 杨长. Cl掺杂对CuI薄膜发光性能增强研究[J]. 无机材料学报, 2023, 38(6): 687-692.
[10]	文志勤, 黄彬荣, 卢涛仪, 邹正光. 压力对PbTiO₃结构和热物性质影响的第一性原理研究[J]. 无机材料学报, 2022, 37(7): 787-794.
[11]	孙铭, 邵溥真, 孙凯, 黄建华, 张强, 修子扬, 肖海英, 武高辉. RGO/Al复合材料界面性质第一性原理研究[J]. 无机材料学报, 2022, 37(6): 651-659.
[12]	肖美霞, 李苗苗, 宋二红, 宋海洋, 李钊, 毕佳颖. 表面端基卤化Ti₃C₂ MXene应用于锂离子电池高容量电极材料的研究[J]. 无机材料学报, 2022, 37(6): 660-668.
[13]	袁罡, 马新国, 贺华, 邓水全, 段汪洋, 程正旺, 邹维. 平面应变对二维单层MoSi₂N₄能带结构和光电性质的影响[J]. 无机材料学报, 2022, 37(5): 527-533.
[14]	冯清影, 刘东, 张莹, 冯浩, 李强. 太阳能驱动的两步热化学循环二氧化碳裂解反应活性材料的热力学与第一性原理评价[J]. 无机材料学报, 2022, 37(2): 223-229.
[15]	张弦, 张策, 姜文君, 冯德强, 姚伟. 四元BiMnVO₅的合成、电子结构与可见光催化性能研究[J]. 无机材料学报, 2022, 37(1): 58-64.