压力对PbTiO3结构和热物性质影响的第一性原理研究

doi:10.15541/jim20210612

摘要/Abstract

摘要：

PbTiO₃是一种重要的铁电功能材料, 但压力对其结构、稳定性、力学和热力学性能的影响尚不明确, 从而限制了其在电子通讯领域的应用。本研究采用基于密度泛函理论的第一性原理方法, 研究了压力下四方铁电相钛酸铅(TP-PTO)、立方顺电相钛酸铅(CP-PTO)、四方前驱体相钛酸铅(PP-PTO)结构和热物性质。研究发现, 三种结构可压缩性由大到小依次为PP-PTO>TP-PTO>CP-PTO。能带结构和态密度均表明PTO在研究的压力范围内未发生相变。PTO带隙随着压力增大逐渐降低, TP-PTO在20 GPa由间接带隙半导体转变为直接带隙半导体, 其余两相在压力下恒为直接带隙半导体。PTO在0~30 Gpa范围力学稳定, 且具有各向异性, 其综合力学性能随着压力的增加而增强, 各向异性则是先降低后升高。通过准谐德拜近似理论研究了温度和压力对PTO德拜温度、熵、热容的影响, 结果表明德拜温度随着温度上升而下降, 随着压力增大而上升, 反映出共价键强度依次为CP-PTO>TP-PTO> PP-PTO。熵和热容随着温度上升而上升, 随着压力的增大而下降。

关键词: 钛酸铅, 电子结构, 弹性力学, 第一性原理

Abstract:

PbTiO₃ (PTO) is an important ferroelectric functional material, but its structure, stability, mechanical property, and thermodynamic property under pressure is still unknown, leading to restriction in applying in the field of electronic communication. Here, first-principles calculations based on density functional theory was performed to study the structure and thermal properties of pre-perovskite phase PbTiO₃ (PP-PTO), ferroelectric tetragonal phase PbTiO₃ (TP-PTO), and paraelectric cubic phase PbTiO₃ (CP-PTO) under pressure. It is found that their compressibility in descending order is PP-PTO>TP-PTO>CP-PTO. Under considered pressure, three PTO phases have not undergone a phase transition analyzed by band structure and density of states, and their band gap gradually decreases with increasing pressure. Among them, the TP-PTO changes from an indirect to a direct band gap semiconductor at 20 GPa, while the others remain a direct band gap semiconductor. Those PTO phases are mechanically stable and anisotropy from 0 to 30 GPa. Furthermore, their comprehensive mechanical properties increase and anisotropy firstly decreases and then increases with increasing pressure. Analysis based on quasi- harmonic Debye approximation theory was performed to study the influence of temperature and pressure on Debye temperature, entropy and heat capacity. The results illuminate that Debye temperature decreases with temperature increase, nevertheless, pressure has the opposite effect, which elucidates that the order of covalent bond from strong to weak is CP-PTO>TP-PTO>PP-PTO. Entropy and heat capacity of PTO increase with rising temperature, but decrease with the increase of pressure.

Key words: PbTiO₃, electronic structure, elastic mechanics, first-principles

中图分类号:

TQ174

文志勤, 黄彬荣, 卢涛仪, 邹正光. 压力对PbTiO₃结构和热物性质影响的第一性原理研究[J]. 无机材料学报, 2022, 37(7): 787-794.

WEN Zhiqin, HUANG Binrong, LU Taoyi, ZOU Zhengguang. Pressure on the Structure and Thermal Properties of PbTiO₃: First-principle Study[J]. Journal of Inorganic Materials, 2022, 37(7): 787-794.

图/表 12

图1 (a) CP-PTO、(b) TP-PTO和(c, d) PP-PTO的晶体结构

Fig. 1 Crystal structures of (a) CP-PTO, (b) TP-PTO and (c, d) PP-PTO

表1 不受压条件下所计算的PTO晶格常数、形成焓及可行的实验和理论计算值

Table 1 Calculated lattice constant and enthalpy of formation of PTO at 0 GPa along with feasible experimental (Exp.) and theoretical calculation (Cal.) values

Phase	Species	Present	Cal.	Exp.
TP-PTO	a=b/nm	0.389	0.389^[18]	0.39^[20]
	c/nm	0.417	0.416^[18]	0.416^[20]
	∆H_f /eV	-13.45	-13.34^[21]
CP-PTO	a=b=c/nm	0.397	0.397^[19]	0.395^[20]
	∆H_f /eV	-13.38	-13.25^[22]
PP-PTO	a=b/nm	1.244	1.216^[10]	1.237^[8]
	c/nm	0.377	0.376^[10]	0.381^[8]
	∆H_f /eV	-5.85

图2 TP-PTO、CP-PTO和PP-PTO体积比(V/V0)随压力的变化曲线

Fig. 2 Variation of TP-PTO, CP-PTO and PP-PTO volume ratios (V/V0) under different pressures

表2 计算0~30 GPa下PTO的带隙值及相关文献报道值

Table 2 Calculated band gap of PTO under 0-30 GPa pressure

	TP-PTO				CP-PTO					PP-PTO
	0 GPa	10 GPa	20 GPa	30 GPa	0 GPa	10 GPa	20 GPa	30 GPa	0 GPa	10 GPa	20 GPa	30 GPa
Present /eV	1.76 ^a	1.587	1.483	1.40	1.675 ^b	1.611	1.538	1.459	2.346 ^c	2.002	1.549	1.142

图3 不同压力下TP-PTO (a)、CP-PTO (b)和PP-PTO (c)的总态密度(TDOS)

Fig. 3 Change of total density of states (TDOS) of TP-PTO (a), CP-PTO (b) and PP-PTO (c) under different pressures

表3 PTO在压力为0的情况下的弹性常数Cij(GPa)及相关的实验和理论计算值

Table 3 Elastic constant (Cij, GPa) of PTO under 0 GPa pressure as well as available experimental (Exp.) and theoretical calculation (Cal.) data

		C₁₁	C₃₃	C₄₄	C₆₆	C₁₂	C₁₃	C₁₆
TP-PTO	Present	252.9	59.1	72.6	100.7	106.1	71.1	-
	Exp.^[34]	237	60	69	144	90	70	-
	Cal.^[18]	253.9	79.8	73.3	100.9	103.8	79	-
CP-PTO	Present	279.2	-	98.2	-	118.5	-	-
	Exp.^[35]	229	-	100	-	101	-	-
	Cal.^[18]	279.9	-	98.6	-	117.9	-	-
PP-PTO	Present	86.95	209.5	50.82	42.28	25.51	49.79	2.55
	Cal.^[9]	98.8	287.8	61.4	56.8	43.2	79.8	4.9

图4 TP-PTO、CP-PTO和PP-PTO的弹性常数(Cij)随压力变化的趋势

Fig. 4 Variation of elastic constants (Cij) of TP-PTO, CP-PTO and PP-PTO with pressure

表4 不同压力下PTO的体模量B、剪切模量G、杨氏模量E、泊松比ν和各向异性Au

Table 4 Bulk modulus (B), shear modulus (G), Young's modulus (E), Poisson's ratio (ν), and anisotropy (Au) of PTO under various pressures

	p/GPa	B/GPa	G/GPa	E/GPa	ν	A^u
TP-PTO	0	87.76	56.91	140.38	0.23	4.1150
	10	211.16	101.92	263.39	0.29	0.1345
	20	274.35	125.99	327.81	0.30	0.0413
	30	315.08	139.28	364.19	0.31	0.1059
CP-PTO	0	172.02	90.86	231.76	0.28	0.0505
	10	217.28	106.87	275.45	0.29	0.0003
	20	257.15	120.49	312.65	0.30	0.0161
	30	299.13	133.24	348.06	0.31	0.0604
PP-PTO	0	63.19	44.09	107.32	0.22	0.7114
	10	121.88	60.96	156.75	0.29	0.5906
	20	173.96	70.31	185.89	0.32	0.4811
	30	219.12	77.26	207.40	0.34	0.5568

图5 TP-PTO、CP-PTO和PP-PTO的德拜温度随压力和温度的变化曲线

Fig. 5 Variation of Debye temperature of TP-PTO, CP-PTO and PP-PTO with pressure and temperature

图6 TP-PTO、CP-PTO、PP-PTO的熵(S)随压力和温度的变化曲线

Fig. 6 Entropy (S) of TP-PTO, CP-PTO and PP-PTO as a function of pressure and temperature

图7 TP-PTO、CP-PTO、PP-PTO定容热容Cv随压力和温度的变化

Fig. 7 Pressure- and temperature-dependent heat capacity at constant volume (Cv) of TP-PTO, CP-PTO and PP-PTO

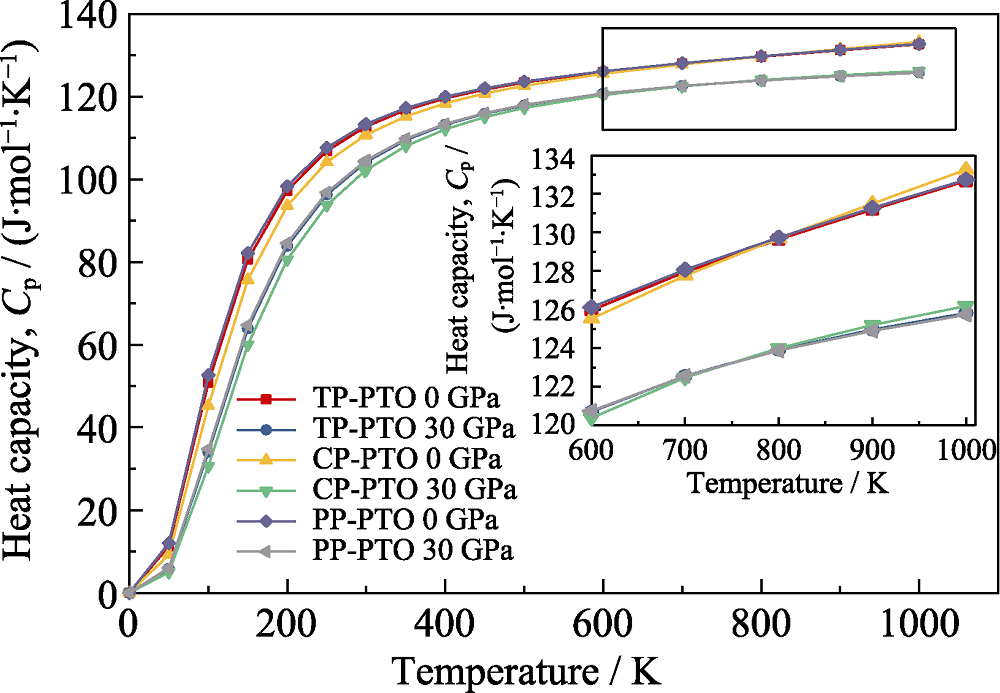
图8 TP-PTO、CP-PTO、PP-PTO定压热容(Cp)随压力和温度的变化

Fig. 8 Pressure- and temperature-dependent heat capacity at constant pressure (Cp) of TP-PTO, CP-PTO and PP-PTO

参考文献 43

[1]	ZHANG S, LI F. High performance ferroelectric relaxor-PbTiO₃ single crystals: status and perspective. Journal of Applied Physics, 2012, 111: 031301.
[2]	HUANG J, ZHANG X W, ZHAO C, et al. Research status of modification of lead titanate series functional ceramics and application of modified ceramics. Materials for Mechanical Engineering, 2021, 45(6): 94-98.
[3]	ZHANG S, LI F, JIANG X, et al. Advantages and challenges of relaxor-PbTiO₃ ferroelectric crystals for electroacoustic transducers-a review. Progress in Materials Science, 2015, 68: 1-66. DOI URL
[4]	KUROIWA Y, AOYAGI S, SAWADA A, et al. Structural study of perovskite-type fine particles by synchrotron radiation powder diffraction. Journal of Thermal Analysis and Calorimetry, 2002, 69(3): 933-938. DOI URL
[5]	WATTANASARN H, SEETAWAN T. Elastic properties and Debye temperature of Zn doped PbTiO₃ from first principles calculation. Integrated Ferroelectrics, 2014, 155(1): 59-65. DOI URL
[6]	PANDECH N, SARASAMAK K, LIMPIJUMNONG S. Sound velocities and elastic properties of PbTiO₃ and PbZrO₃ under pressure: first principles study. Ceramics International, 2013, 39: S277-S281.
[7]	YASEEN M, AMBREEN H, MEHMOOD R, et al. Investigation of optical and thermoelectric properties of PbTiO₃ under pressure. Physica B: Condensed Matter, 2021, 615: 412857.
[8]	REN Z, XU G, LIU Y, et al. PbTiO₃ nanofibers with edge-shared TiO₆ octahedra. Journal of the American Chemical Society, 2010, 132(16): 5572-5573. DOI URL
[9]	LIU Y, NI L H, REN Z H, et al. First-principles study of structural stability and elastic property of pre-perovskite PbTiO₃. Chinese Physics B, 2012, 21(1): 352-356.
[10]	ZHOU M J, WANG Y, JI Y, et al. First-principles lattice dynamics and thermodynamic properties of pre-perovskite PbTiO₃. Acta Materialia, 2019, 171: 146-153. DOI URL
[11]	PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple. Physical Review Letters, 1996, 77(18): 3865-3868. DOI URL
[12]	PERDEW J P, RUZSINSZKY A, CSONKA G I, et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Physical Review Letters, 2008, 100(13): 136406.
[13]	LIU Y, NI L H, XU G, et al. Phase transition in PbTiO₃ under pressure studied by the first-principles method. Physica B-Condensed Matter, 2008, 403(21/22): 3863-3866. DOI URL
[14]	SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code. Journal of Physics: Condensed Matter, 2002, 14(11): 2717-2744. DOI URL
[15]	PERDEW J P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Physical Review B, 1986, 33(12): 8822-8824. DOI URL
[16]	LAASONEN K, PASQUARELLO A, CAR R, et al. Carparrinello molecular dynamics with vanderbilt ultrasoft pseudopotentials. Physical Review B, 1993, 47(16): 10142-10153. DOI URL
[17]	FISCHER T H, ALMLOF J. General methods for geometry and wave function optimization. The Journal of Physical Chemistry, 1992, 96(24): 9768-9774. DOI URL
[18]	LONG J, YANG L, WEI X. Lattice, elastic properties and Debye temperatures of ATiO₃ (A=Ba, Ca, Pb, Sr) from first-principles. Journal of Alloys and Compounds, 2013, 549: 336-340. DOI URL
[19]	ZHANG Y, SUN J, PERDEW J P, et al. Comparative first- principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA. Physical Review B, 2017, 96: 035143.
[20]	NELMES R J, KUHS W F. The crystal structure of tetragonal PbTiO₃ at room temperature and at 700 K. Solid State Communications, 1985, 54(8): 721-723. DOI URL
[21]	ALAHMED Z, FU H X. First-principles determination of chemical potentials and vacancy formation energies in PbTiO₃ and BaTiO₃. Physical Review B, 2007, 76(22): 224101.
[22]	NIU P J, YAN J L, XU C Y. First-principles study of nitrogen doping and oxygen vacancy in cubic PbTiO₃. Computational Materials Science, 2015, 98: 10-14. DOI URL
[23]	WEN Z, ZHAO Y, LI J, et al. Phase stability and thermo-physical properties of nickel-aluminum binary chemically disordered systems via first-principles study. Metals and Materials International, 2021, 27(6): 1469-1477. DOI URL
[24]	JIAO Z Y, YANG J F, ZHANG X Z, et al. Theoretical investigation of elastic, electronic, and optical properties of zinc-blende structure GaN under high pressure. Acta Physica Sinica, 2011, 60(11): 534-541.
[25]	HOSSEINI S M, MOVLAROOY T, KOMPANY A. First-principle calculations of the cohesive energy and the electronic properties of PbTiO₃. Physica B: Condensed Matter, 2007, 391(2): 316-321. DOI URL
[26]	SHI Y J, DU Y L, CHEN G, et al. First principle study on phase stability and electronic structure of YCu. Physics Letters A, 2007, 368(6): 495-498. DOI URL
[27]	HU Q M, YANG R, XU D S, et al. Energetics and electronic structure of grain boundaries and surfaces of B- and H-doped Ni₃Al. Physical Review B, 2003, 67(22): 224203.
[28]	GUO F, ZHOU X, LI G, et al. Structural, mechanical, electronic and thermodynamic properties of cubic TiC compounds under different pressures: a first-principles study. Solid State Communications, 2020, 311: 113856.
[29]	ZAMETIN V I. Absorption edge anomalies in polar semiconductors and dielectrics at phase transitions. Physica Status Solidi (B), 1984, 124(2): 625-640. DOI URL
[30]	LEITE E R, SANTOS L P S, CARRENO N L V, et al. Photoluminescence of nanostructured PbTiO₃ processed by high- energy mechanical milling. Applied Physics Letters, 2001, 78(15): 2148-2150. DOI URL
[31]	REN Z, JING G, LIU Y, et al. Pre-perovskite nanofiber: a new direct-band gap semiconductor with green and near infrared photoluminescence. RSC Advances, 2013, 3(16): 5453-5458. DOI URL
[32]	YANG A C M. Measurements of equi-biaxial stress in adhered polyimide films by tilted beam polarized light microscopy. Materials Chemistry and Physics, 1995, 41(2): 150-153. DOI URL
[33]	DAI S, LIU W. First-principles study on the structural, mechanical and electronic properties of δ and γ phases in Inconel 718. Computational Materials Science, 2010, 49(2): 414-418. DOI URL
[34]	KALINICHEV A G, BASS J D, SUN B N, et al. Elastic properties of tetragonal PbTiO₃ single crystals by brillouin scattering. Journal of Materials Research, 1997, 12(10): 2623-2627. DOI URL
[35]	LI Z, GRIMSDITCH M, FOSTER C M, et al. Dielectric and elastic properties of ferroelectric materials at elevated temperature. Journal of Physics and Chemistry of Solids, 1996, 57(10): 1433-1438. DOI URL
[36]	HILL R. The elastic behaviour of a crystalline aggregate. Proceedings of the Physical Society. Section A, 1952, 65(5): 349-354. DOI URL
[37]	VOIGT W. Ueber die beziehung zwischen den beiden elasticitätsconstanten isotroper körper. Annalen der Physik, 1889, 274(12): 573-587. DOI URL
[38]	WANG H J, SU X P, SUN S P, et al. First-principles calculations to investigate the anisotropic elasticity and thermodynamic properties of FeAl₃ under pressure effect. Results in Physics, 2021, 26: 104361.
[39]	ZHANG R, GAO P, WANG X, et al. Pressure and temperature dependence of structural and elastic properties of FeSe superconductor by first-principles calculation. Cryogenics, 2019, 102: 28-34. DOI URL
[40]	PENG J H, TIKHONOV E. Vacancy on structures, mechanical properties and electronic properties of ternary Hf-Ta-C system: a first-principles study. Journal of Inorganic Materials, 2022, 37(1): 51-57. DOI URL
[41]	RANGANATHAN S I, OSTOJA-STARZEWSKI M. Universal elastic anisotropy index. Physical Review Letters, 2008, 101(5): 055504.
[42]	BLANCO M A, FRANCISCO E, LUAÑA V. Gibbs: isothermal- isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model. Computer Physics Communications, 2004, 158(1): 57-72. DOI URL
[43]	OTERO-DE-LA-ROZA A, ABBASI-PÉREZ D, LUAÑA V. Gibbs 2: a new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Computer Physics Communications, 2011, 182(10): 2232-2248. DOI URL

压力对PbTiO₃结构和热物性质影响的第一性原理研究

Pressure on the Structure and Thermal Properties of PbTiO₃: First-principle Study

RichHTML

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

图/表 12

参考文献 43

相关文章 15

编辑推荐

Metrics

本文评价

[1]	吴玉豪, 彭仁赐, 程春玉, 杨丽, 周益春. Hf_xTa_1-_xC体系力学性能及熔化曲线的第一性原理研究[J]. 无机材料学报, 2024, 39(7): 761-768.
[2]	靳宇翔, 宋二红, 朱永福. 3d过渡金属单原子掺杂石墨烯缺陷电催化还原CO₂的第一性原理研究[J]. 无机材料学报, 2024, 39(7): 845-852.
[3]	王伟华, 张磊宁, 丁峰, 代兵, 韩杰才, 朱嘉琦, 贾怡, 杨宇. 铱衬底上金刚石外延形核与生长: 第一性原理计算[J]. 无机材料学报, 2024, 39(4): 416-422.
[4]	张宇晨, 陆知遥, 赫晓东, 宋广平, 朱春城, 郑永挺, 柏跃磊. 硫族MAX相硼化物的物相稳定性和性能预测[J]. 无机材料学报, 2024, 39(2): 225-232.
[5]	陈梦杰, 王倩倩, 吴成铁, 黄健. 基于DFT的描述符预测生物陶瓷的降解性[J]. 无机材料学报, 2024, 39(10): 1175-1181.
[6]	周云凯, 刁亚琪, 王明磊, 张宴会, 王利民. 聚苯胺改性Ti₃C₂(OH)₂抗氧化性的第一性原理计算研究[J]. 无机材料学报, 2024, 39(10): 1151-1158.
[7]	吴晓维, 张涵, 曾彪, 明辰, 孙宜阳. 杂化泛函HSE和PBE0计算CsPbI₃缺陷性质的比较研究[J]. 无机材料学报, 2023, 38(9): 1110-1116.
[8]	王雪瑶, 王武港, 李应卫, 彭奇, 梁瑞虹. PZT陶瓷本构行为与断裂性能的相关性研究[J]. 无机材料学报, 2023, 38(7): 839-844.
[9]	张守超, 陈洪雨, 刘洪飞, 杨羽, 李欣, 刘德峰. 6H-SiC中子辐照肿胀高温回复及光学特性研究[J]. 无机材料学报, 2023, 38(6): 678-686.
[10]	杨颖康, 邵怡晴, 李柏良, 吕志伟, 王路路, 王亮君, 曹逊, 吴宇宁, 黄荣, 杨长. Cl掺杂对CuI薄膜发光性能增强研究[J]. 无机材料学报, 2023, 38(6): 687-692.
[11]	孙铭, 邵溥真, 孙凯, 黄建华, 张强, 修子扬, 肖海英, 武高辉. RGO/Al复合材料界面性质第一性原理研究[J]. 无机材料学报, 2022, 37(6): 651-659.
[12]	肖美霞, 李苗苗, 宋二红, 宋海洋, 李钊, 毕佳颖. 表面端基卤化Ti₃C₂ MXene应用于锂离子电池高容量电极材料的研究[J]. 无机材料学报, 2022, 37(6): 660-668.
[13]	袁罡, 马新国, 贺华, 邓水全, 段汪洋, 程正旺, 邹维. 平面应变对二维单层MoSi₂N₄能带结构和光电性质的影响[J]. 无机材料学报, 2022, 37(5): 527-533.
[14]	冯清影, 刘东, 张莹, 冯浩, 李强. 太阳能驱动的两步热化学循环二氧化碳裂解反应活性材料的热力学与第一性原理评价[J]. 无机材料学报, 2022, 37(2): 223-229.
[15]	张弦, 张策, 姜文君, 冯德强, 姚伟. 四元BiMnVO₅的合成、电子结构与可见光催化性能研究[J]. 无机材料学报, 2022, 37(1): 58-64.