
Journal of Inorganic Materials ›› 2025, Vol. 40 ›› Issue (12): 1387-1394.DOI: 10.15541/jim20250027
• RESEARCH ARTICLE • Previous Articles Next Articles
ZHAO Lijuan1,2( ), TAN Zhe1,2, ZHANG Xiaoguang1,2(
), TAN Zhe1,2, ZHANG Xiaoguang1,2( ), JIANG Guosai1,2, TAO Ran1,2, PAN De’an2,3,4(
), JIANG Guosai1,2, TAO Ran1,2, PAN De’an2,3,4( )
)
Received:2025-01-18
Revised:2025-04-15
Published:2025-12-20
Online:2025-05-09
Contact:
ZHANG Xiaoguang, professor. E-mail: zhangxg@bjut.edu.cn;About author:ZHAO Lijuan (1997-), female, PhD candidate. E-mail: zhaolijuan97@163.com
Supported by:CLC Number:
ZHAO Lijuan, TAN Zhe, ZHANG Xiaoguang, JIANG Guosai, TAO Ran, PAN De’an. Numerical Simulation of Particle Classification for Spent Hydrogenation Catalyst[J]. Journal of Inorganic Materials, 2025, 40(12): 1387-1394.

Fig. 2 Analysis of (a1, b1) theoretical derivation and (a2, b2) simulation (a1, a2) dp=0.29 mm; (b1, b2) dp=2.19 mm. Colorful figures are available on website

Fig. 4 Effects of (a1, a2) gas velocity, (b1, b2) inlet height, and (c1, c2) feed flow on (a1, b1, c1) grading efficiency and (a2, b2, c2) minimum particle diameter in the product collection section Colorful figures are available on website

Fig. 5 Model residual analysis (a) Normal probability versus externally studentized residual; (b) Externally studentized residual versus predicted value; (c) Externally studentized residual versus run number; (d) Predicted value versus actual value. Colorful figures are available on website
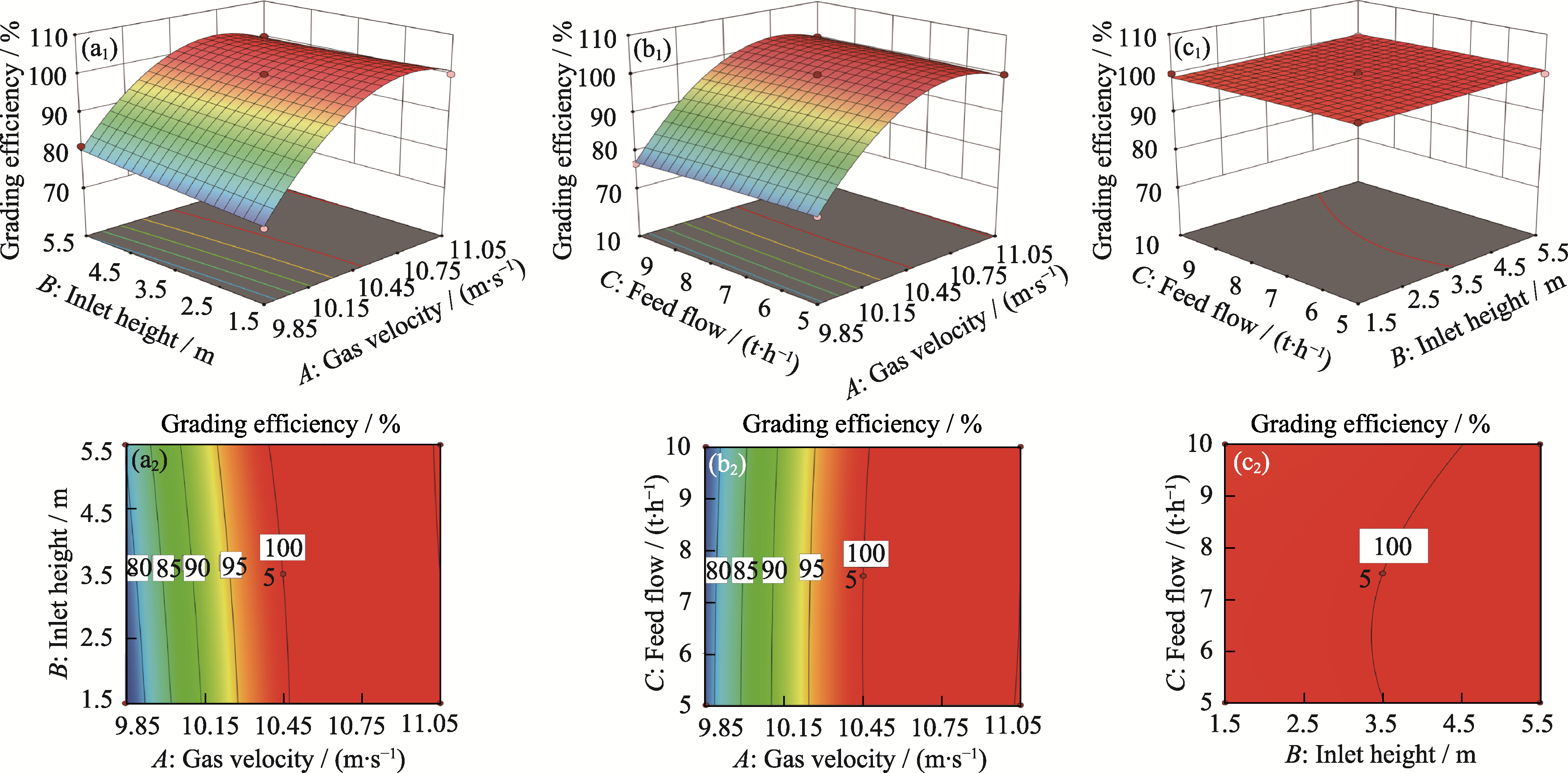
Fig. 6 Response surface analysis (a1, a2) Factors gas velocity A and inlet height B; (b1, b2) Factors gas velocity A and feed flow C; (c1, c2) Factors inlet height B and feed flow C;(a1, b1, c1) Response surface; (a2, b2, c2) Contour plots. Colorful figures are available on website
| Average mass conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=0$ |
|---|
| Average momentum conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=-\alpha_{\mathrm{g}} \nabla P+\nabla \cdot\left(\alpha_{\mathrm{g}} \tau_{\mathrm{g}}\right)+F_{\mathrm{p} \rightarrow \mathrm{~g}}+\alpha_{\mathrm{g}} \rho_{\mathrm{g}} g$ |
| Velocity vector of the gas phase: $\tau_{\mathrm{g}}=\mu_{\mathrm{g}}\left(\nabla \boldsymbol{v}_{\mathrm{g}}+\nabla \boldsymbol{v}_{\mathrm{g}}^{T}\right)-2 / 3 \cdot\left(\nabla \boldsymbol{v}_{\mathrm{g}}\right) \boldsymbol{I}$ |
| Gas phase density: $\rho_{\mathrm{g}}=P_{\mathrm{g}} M / R_{\mathrm{g}} T$ |
| Momentum source term interacting with the particle phase: $F_{\mathrm{p} \rightarrow \mathrm{~g}}=-\sum_{p=1}^{n} F_{\mathrm{g} \rightarrow \mathrm{p}} / V_{\mathrm{C}}$ |
| Force generated by the gas phase on the particles: $F_{\mathrm{g} \rightarrow \mathrm{p}}=F_{\mathrm{D}}+F_{\nabla P}$ |
| Pressure gradient force $F_{\nabla P}$: $F_{\nabla P}=-V_{\mathrm{p}} \nabla P$ |
| Drag force calculation when using CGM: $F_{\mathrm{D}, \mathrm{CGM}}=1 / 2 \cdot\left(f_{\mathrm{CGM}}^{3} C_{\mathrm{D}} \rho_{\mathrm{g}} A^{\prime}\left|\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right|\left(\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right)\right)$ |
| Where $C_{D}$ is the drag coefficient, expressed as: $C_{\mathrm{D}}=\psi C_{\mathrm{D} 1}+(1-\psi) C_{\mathrm{D} 2}$ |
| Where $\psi$ is the mixing parameter, calculated by: $\psi=1 / \pi \cdot \tan ^{-1}\left[150 \cdot 1.75\left(0.8-\alpha_{\mathrm{g}}\right)\right]+0.5$ |
| Where $C_{\mathrm{D} 1}$ is expressed as: $C_{\mathrm{D} 1}=200 \alpha_{\mathrm{p}} / \alpha_{\mathrm{g}} \phi^{2} R e+7 / 3 \phi$ |
| Where $\psi$ is the sphericity of the particles, defined as: $\phi=A_{\mathrm{sph}} / A_{\mathrm{p}}$ |
| Where $C_{\mathrm{D} 2}$ is expressed as: $C_{\mathrm{D} 2}=\alpha_{\mathrm{g}}^{-1.65} \max \left\{24 / \alpha_{\mathrm{g}} R e_{\mathrm{p}} \cdot\left[1+0.15\left(\alpha_{\mathrm{g}} R e_{\mathrm{p}}\right)^{0.687}\right], 0.44\right\}$ |
| Particle relative Reynolds number $R e_{\mathrm{p}}$ when using CGM: $R e_{\mathrm{p}, \mathrm{CGM}}=\rho_{\mathrm{g}}\left|\boldsymbol{v}_{\mathrm{p}}-\boldsymbol{v}_{\mathrm{g}}\right| d_{\mathrm{p}, \mathrm{CGM}} / f_{\mathrm{CGM}} \mu_{\mathrm{g}}$ |
Table S1 Main equations in coarse-grained CFD-DEM method
| Average mass conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=0$ |
|---|
| Average momentum conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=-\alpha_{\mathrm{g}} \nabla P+\nabla \cdot\left(\alpha_{\mathrm{g}} \tau_{\mathrm{g}}\right)+F_{\mathrm{p} \rightarrow \mathrm{~g}}+\alpha_{\mathrm{g}} \rho_{\mathrm{g}} g$ |
| Velocity vector of the gas phase: $\tau_{\mathrm{g}}=\mu_{\mathrm{g}}\left(\nabla \boldsymbol{v}_{\mathrm{g}}+\nabla \boldsymbol{v}_{\mathrm{g}}^{T}\right)-2 / 3 \cdot\left(\nabla \boldsymbol{v}_{\mathrm{g}}\right) \boldsymbol{I}$ |
| Gas phase density: $\rho_{\mathrm{g}}=P_{\mathrm{g}} M / R_{\mathrm{g}} T$ |
| Momentum source term interacting with the particle phase: $F_{\mathrm{p} \rightarrow \mathrm{~g}}=-\sum_{p=1}^{n} F_{\mathrm{g} \rightarrow \mathrm{p}} / V_{\mathrm{C}}$ |
| Force generated by the gas phase on the particles: $F_{\mathrm{g} \rightarrow \mathrm{p}}=F_{\mathrm{D}}+F_{\nabla P}$ |
| Pressure gradient force $F_{\nabla P}$: $F_{\nabla P}=-V_{\mathrm{p}} \nabla P$ |
| Drag force calculation when using CGM: $F_{\mathrm{D}, \mathrm{CGM}}=1 / 2 \cdot\left(f_{\mathrm{CGM}}^{3} C_{\mathrm{D}} \rho_{\mathrm{g}} A^{\prime}\left|\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right|\left(\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right)\right)$ |
| Where $C_{D}$ is the drag coefficient, expressed as: $C_{\mathrm{D}}=\psi C_{\mathrm{D} 1}+(1-\psi) C_{\mathrm{D} 2}$ |
| Where $\psi$ is the mixing parameter, calculated by: $\psi=1 / \pi \cdot \tan ^{-1}\left[150 \cdot 1.75\left(0.8-\alpha_{\mathrm{g}}\right)\right]+0.5$ |
| Where $C_{\mathrm{D} 1}$ is expressed as: $C_{\mathrm{D} 1}=200 \alpha_{\mathrm{p}} / \alpha_{\mathrm{g}} \phi^{2} R e+7 / 3 \phi$ |
| Where $\psi$ is the sphericity of the particles, defined as: $\phi=A_{\mathrm{sph}} / A_{\mathrm{p}}$ |
| Where $C_{\mathrm{D} 2}$ is expressed as: $C_{\mathrm{D} 2}=\alpha_{\mathrm{g}}^{-1.65} \max \left\{24 / \alpha_{\mathrm{g}} R e_{\mathrm{p}} \cdot\left[1+0.15\left(\alpha_{\mathrm{g}} R e_{\mathrm{p}}\right)^{0.687}\right], 0.44\right\}$ |
| Particle relative Reynolds number $R e_{\mathrm{p}}$ when using CGM: $R e_{\mathrm{p}, \mathrm{CGM}}=\rho_{\mathrm{g}}\left|\boldsymbol{v}_{\mathrm{p}}-\boldsymbol{v}_{\mathrm{g}}\right| d_{\mathrm{p}, \mathrm{CGM}} / f_{\mathrm{CGM}} \mu_{\mathrm{g}}$ |
| Symbol | Physical significance |
|---|---|
| $g$ | Gas phase |
| $p$ | Particle phase |
| $\alpha_{\mathrm{p}}$ | Concentration of the particulate phase |
| $\rho_{\mathrm{g}}$ | Density of the gas phase |
| $\rho_{\mathrm{p}}$ | Density of the particulate phase |
| $V_{\mathrm{g}}$ | Velocity vector of the gas phase |
| $V_{\mathrm{p}}$ | Velocity vector of the particulate phase |
| $\tau_{\mathrm{g}}$ | Viscous stress tensor of the gas phase |
| $T$ | Temperature of the gas phase |
| $I$ | Identity matrix |
| $P_{g}$ | Pressure of the gas |
| $n$ | Number of particles inside the computational cell volume |
| $V_{C}$ | Computational cell volume |
| $F_{\mathrm{p} \rightarrow \mathrm{~g}}$ | Force generated by the particles on the gas phase |
| F_{\mathrm{g} \rightarrow \mathrm{~p}} | Force generated by the gas phase on the particulate phase |
| $F_{D}$ | Drag force |
| $F_{\nabla P}$ | Pressure gradient force |
| $V_{p}$ | Volume of the particle |
| $\nabla p$ | Local pressure gradient |
| $A'$ | Projected particle area in the flow direction |
| $f_{\mathrm{CGM}}$ | Scale factor of the coarse particle |
| $f_{\mathrm{D,CGM}}$ | Drag force of the coarse particle |
| $C_{D}$ | Drag coefficient |
| $\psi$ | Mixing parameter |
| $\phi$ | Sphericity of the particles |
| $A_{sph}$ | Surface area of a sphere with the same volume as the particle |
| $A_{p}$ | Actual surface area of the particle |
| $R e_{\mathrm{p}, \mathrm{CGM}}$ | Particle relative Reynolds number of the coarse particle |
| $d_{\mathrm{p}, \mathrm{CGM}}$ | Diameter of the coarse particle |
| $\mu_{\mathrm{g}}$ | Viscosity of gas phase |
| $d_{p}$ | Spherical equivalent diameter of the particle |
| $V_{HDS}$ | Volume of the spent hydrogenation (HDS) catalyst rod particle |
| $t$ | Graded time of the spent HDS catalyst particles |
| $G$ | Gravity of the spent HDS catalyst particles |
| $m$ | Mass of the spent HDS catalyst particles |
| $g$ | Acceleration due to gravity |
| $α$ | Acceleration of the particle |
| $V_{pi}$ | Velocity of a particle dropped from the inlet at i second |
| $V_{gi}$ | Cross-sectional gas velocity at i second |
| $α_{i}$ | Acceleration of a particle dropped from the inlet at i second |
| $L_{i}$ | Distance of a particle dropped from the inlet at i second |
| $\lambda$ | Gradation efficiency |
| $N_{1}$ | Number of the spent HDS catalyst particles with a diameter greater than 1.5 mm in the product collection section |
| $N_{2}$ | Total number of spent HDS catalyst particles in the product collection section |
Table S2 Nomenclature of the symbols
| Symbol | Physical significance |
|---|---|
| $g$ | Gas phase |
| $p$ | Particle phase |
| $\alpha_{\mathrm{p}}$ | Concentration of the particulate phase |
| $\rho_{\mathrm{g}}$ | Density of the gas phase |
| $\rho_{\mathrm{p}}$ | Density of the particulate phase |
| $V_{\mathrm{g}}$ | Velocity vector of the gas phase |
| $V_{\mathrm{p}}$ | Velocity vector of the particulate phase |
| $\tau_{\mathrm{g}}$ | Viscous stress tensor of the gas phase |
| $T$ | Temperature of the gas phase |
| $I$ | Identity matrix |
| $P_{g}$ | Pressure of the gas |
| $n$ | Number of particles inside the computational cell volume |
| $V_{C}$ | Computational cell volume |
| $F_{\mathrm{p} \rightarrow \mathrm{~g}}$ | Force generated by the particles on the gas phase |
| F_{\mathrm{g} \rightarrow \mathrm{~p}} | Force generated by the gas phase on the particulate phase |
| $F_{D}$ | Drag force |
| $F_{\nabla P}$ | Pressure gradient force |
| $V_{p}$ | Volume of the particle |
| $\nabla p$ | Local pressure gradient |
| $A'$ | Projected particle area in the flow direction |
| $f_{\mathrm{CGM}}$ | Scale factor of the coarse particle |
| $f_{\mathrm{D,CGM}}$ | Drag force of the coarse particle |
| $C_{D}$ | Drag coefficient |
| $\psi$ | Mixing parameter |
| $\phi$ | Sphericity of the particles |
| $A_{sph}$ | Surface area of a sphere with the same volume as the particle |
| $A_{p}$ | Actual surface area of the particle |
| $R e_{\mathrm{p}, \mathrm{CGM}}$ | Particle relative Reynolds number of the coarse particle |
| $d_{\mathrm{p}, \mathrm{CGM}}$ | Diameter of the coarse particle |
| $\mu_{\mathrm{g}}$ | Viscosity of gas phase |
| $d_{p}$ | Spherical equivalent diameter of the particle |
| $V_{HDS}$ | Volume of the spent hydrogenation (HDS) catalyst rod particle |
| $t$ | Graded time of the spent HDS catalyst particles |
| $G$ | Gravity of the spent HDS catalyst particles |
| $m$ | Mass of the spent HDS catalyst particles |
| $g$ | Acceleration due to gravity |
| $α$ | Acceleration of the particle |
| $V_{pi}$ | Velocity of a particle dropped from the inlet at i second |
| $V_{gi}$ | Cross-sectional gas velocity at i second |
| $α_{i}$ | Acceleration of a particle dropped from the inlet at i second |
| $L_{i}$ | Distance of a particle dropped from the inlet at i second |
| $\lambda$ | Gradation efficiency |
| $N_{1}$ | Number of the spent HDS catalyst particles with a diameter greater than 1.5 mm in the product collection section |
| $N_{2}$ | Total number of spent HDS catalyst particles in the product collection section |
| Diameter/mm | Percentage/% |
|---|---|
| 0.29 | 1.00 |
| 1.14 | 3.04 |
| 1.44 | 35.50 |
| 1.65 | 34.28 |
| 1.82 | 14.81 |
| 1.96 | 6.03 |
| 2.08 | 3.45 |
| 2.19 | 1.89 |
Table S3 Composition of particles
| Diameter/mm | Percentage/% |
|---|---|
| 0.29 | 1.00 |
| 1.14 | 3.04 |
| 1.44 | 35.50 |
| 1.65 | 34.28 |
| 1.82 | 14.81 |
| 1.96 | 6.03 |
| 2.08 | 3.45 |
| 2.19 | 1.89 |
| Diameter/mm | Velocity/(m·s-1) |
|---|---|
| 1.14 | 8.23 |
| 1.44 | 9.25 |
| 1.65 | 9.90 |
| 1.82 | 10.39 |
| 1.96 | 10.79 |
| 2.08 | 11.11 |
| 2.19 | 11.40 |
Table S4 Critical gas velocity required for particle gradation
| Diameter/mm | Velocity/(m·s-1) |
|---|---|
| 1.14 | 8.23 |
| 1.44 | 9.25 |
| 1.65 | 9.90 |
| 1.82 | 10.39 |
| 1.96 | 10.79 |
| 2.08 | 11.11 |
| 2.19 | 11.40 |
| Physical property | Value |
|---|---|
| fCGM | 7 |
| Particle temperature | 300 K |
| Gas velocity | 9.25 m/s |
| Feed flow | 1.25 t /h |
| Inlet height | 3.50 m |
Table S5 Boundary conditions of model validation for the fluidized graded bed
| Physical property | Value |
|---|---|
| fCGM | 7 |
| Particle temperature | 300 K |
| Gas velocity | 9.25 m/s |
| Feed flow | 1.25 t /h |
| Inlet height | 3.50 m |
| Independent variable | Unit | Symbol | Factor level | ||
|---|---|---|---|---|---|
| -1 | 0 | -1 | |||
| Gas velocity | m/s | A | 9.85 | 10.45 | 11.05 |
| Inlet height | m | B | 1.5 | 3.5 | 5.5 |
| Feed flow | t/h | C | 5 | 7.5 | 10 |
Table S6 Three-factor and three-level for BBD
| Independent variable | Unit | Symbol | Factor level | ||
|---|---|---|---|---|---|
| -1 | 0 | -1 | |||
| Gas velocity | m/s | A | 9.85 | 10.45 | 11.05 |
| Inlet height | m | B | 1.5 | 3.5 | 5.5 |
| Feed flow | t/h | C | 5 | 7.5 | 10 |
| NO. | Independent variable | Response value | ||
|---|---|---|---|---|
| Gas velocity, A/(m·s-1) | Inlet height, B/m | Feed flow, C/(t·h-1) | Grading efficiency, $\lambda$/% | |
| 1 | 10.45 | 3.5 | 7.5 | 100 |
| 2 | 9.85 | 1.5 | 7.5 | 75.37 |
| 3 | 11.05 | 5.5 | 7.5 | 100 |
| 4 | 10.45 | 3.5 | 7.5 | 100 |
| 5 | 10.45 | 3.5 | 7.5 | 100 |
| 6 | 11.05 | 3.5 | 10 | 100 |
| 7 | 10.45 | 5.5 | 10 | 100 |
| 8 | 9.85 | 3.5 | 10 | 76.56 |
| 9 | 10.45 | 1.5 | 10 | 100 |
| 10 | 10.45 | 3.5 | 7.5 | 100 |
| 11 | 10.45 | 5.5 | 5 | 100 |
| 12 | 9.85 | 5.5 | 7.5 | 81.17 |
| 13 | 10.45 | 1.5 | 5 | 100 |
| 14 | 11.05 | 3.5 | 5 | 100 |
| 15 | 9.85 | 3.5 | 5 | 78.24 |
| 16 | 10.45 | 3.5 | 7.5 | 100 |
| 17 | 11.05 | 1.5 | 7.5 | 100 |
Table S7 Design and simulation results of RSM of grading efficiency
| NO. | Independent variable | Response value | ||
|---|---|---|---|---|
| Gas velocity, A/(m·s-1) | Inlet height, B/m | Feed flow, C/(t·h-1) | Grading efficiency, $\lambda$/% | |
| 1 | 10.45 | 3.5 | 7.5 | 100 |
| 2 | 9.85 | 1.5 | 7.5 | 75.37 |
| 3 | 11.05 | 5.5 | 7.5 | 100 |
| 4 | 10.45 | 3.5 | 7.5 | 100 |
| 5 | 10.45 | 3.5 | 7.5 | 100 |
| 6 | 11.05 | 3.5 | 10 | 100 |
| 7 | 10.45 | 5.5 | 10 | 100 |
| 8 | 9.85 | 3.5 | 10 | 76.56 |
| 9 | 10.45 | 1.5 | 10 | 100 |
| 10 | 10.45 | 3.5 | 7.5 | 100 |
| 11 | 10.45 | 5.5 | 5 | 100 |
| 12 | 9.85 | 5.5 | 7.5 | 81.17 |
| 13 | 10.45 | 1.5 | 5 | 100 |
| 14 | 11.05 | 3.5 | 5 | 100 |
| 15 | 9.85 | 3.5 | 5 | 78.24 |
| 16 | 10.45 | 3.5 | 7.5 | 100 |
| 17 | 11.05 | 1.5 | 7.5 | 100 |
| Standard deviation | Mean | Coefficient of variance/% | R2 | Adj. R2 | Pred. R2 | Adeq Precision |
|---|---|---|---|---|---|---|
| 0.8397 | 94.78 | 0.8860 | 0.9968 | 0.9926 | 0.9481 | 38.9173 |
Table S8 Model fit statistics
| Standard deviation | Mean | Coefficient of variance/% | R2 | Adj. R2 | Pred. R2 | Adeq Precision |
|---|---|---|---|---|---|---|
| 0.8397 | 94.78 | 0.8860 | 0.9968 | 0.9926 | 0.9481 | 38.9173 |
| Source | Coefficient estimate | Sum of squares | Degree of freedom | Mean square | F value | P value |
|---|---|---|---|---|---|---|
| Model | - | 1516.81 | 9 | 168.53 | 239.00 | <0.0001 |
| A | 11.0825 | 982.57 | 1 | 982.57 | 1393.37 | <0.0001 |
| B | 0.725 | 4.21 | 1 | 4.21 | 5.96 | 0.0446 |
| C | -0.21 | 0.3528 | 1 | 0.3528 | 0.5003 | 0.5022 |
| AB | -1.45 | 8.41 | 1 | 8.41 | 11.93 | 0.0106 |
| AC | 0.42 | 0.7056 | 1 | 0.7056 | 1 | 0.3505 |
| BC | -8.71×10-16 | 0 | 1 | 0 | 0 | 1 |
| A2 | -11.0825 | 517.14 | 1 | 517.14 | 733.35 | <0.0001 |
| B2 | 0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| C2 | -0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
Table S9 ANOVA results of the regression equation
| Source | Coefficient estimate | Sum of squares | Degree of freedom | Mean square | F value | P value |
|---|---|---|---|---|---|---|
| Model | - | 1516.81 | 9 | 168.53 | 239.00 | <0.0001 |
| A | 11.0825 | 982.57 | 1 | 982.57 | 1393.37 | <0.0001 |
| B | 0.725 | 4.21 | 1 | 4.21 | 5.96 | 0.0446 |
| C | -0.21 | 0.3528 | 1 | 0.3528 | 0.5003 | 0.5022 |
| AB | -1.45 | 8.41 | 1 | 8.41 | 11.93 | 0.0106 |
| AC | 0.42 | 0.7056 | 1 | 0.7056 | 1 | 0.3505 |
| BC | -8.71×10-16 | 0 | 1 | 0 | 0 | 1 |
| A2 | -11.0825 | 517.14 | 1 | 517.14 | 733.35 | <0.0001 |
| B2 | 0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| C2 | -0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| [1] |
TRAN T T, LEE M S. Separation of Mo(VI), V(V), Ni(II), Al(III) from synthetic hydrochloric acidic leaching solution of spent catalysts by solvent extraction with ionic liquid. Separation and Purification Technology, 2020, 247: 117005.
DOI URL |
| [2] |
VALVERDE I M, PAULINO J F, AFONSO J C. Hydrometallurgical route to recover molybdenum, nickel, cobalt and aluminum from spent hydrotreating catalysts in sulphuric acid medium. Journal of Hazardous Materials, 2008, 160(2/3): 310.
DOI PMID |
| [3] |
WANG W Q, ZHANG L, HAN Y, et al. Cleaner recycling of spent Ni-Mo/γ-Al2O3 catalyst based on mineral phase reconstruction. Journal of Cleaner Production, 2019, 232: 266.
DOI URL |
| [4] |
WANG J Z, WANG S N, OLAYIWOLA A, et al. Recovering valuable metals from spent hydrodesulfurization catalyst via blank roasting and alkaline leaching. Journal of Hazardous Materials, 2021, 416: 125849.
DOI URL |
| [5] |
LIANG X, TANG J J, LI L S, et al. A review of metallurgical processes and purification techniques for recovering Mo, V, Ni, Co, Al from spent catalysts. Journal of Cleaner Production, 2022, 376: 134108.
DOI URL |
| [6] | 窦中堃, 张家靓, 陈永强, 等. 废加氢催化剂熔炼合金酸浸液中钼、镍萃取分离研究. 有色金属科学与工程, 2024, 15(1): 1. |
| [7] | ARSLANOĞLU H, YARAŞ A. Recovery of molybdenum, cobalt and nickel from spent hydrodesulphurization catalyst through oxidizing roast followed by sodium persulfate leaching. Sustainable Materials and Technologies, 2021, 28: e00286. |
| [8] | BARIK S P, PARK K H, PARHI P K, et al. Direct leaching of molybdenum and cobalt from spent hydrodesulphurization catalyst with sulphuric acid. Hydrometallurgy, 2012, 111: 46. |
| [9] |
HE R Y, LI D, YANG K P, et al. Process optimization and modeling of recycling Mo (VI) from spent Mo-Fe2O3/Al2O3 catalyst by roasting with sodium carbonate using response surface methodology (RSM). International Journal of Refractory Metals and Hard Materials, 2020, 87: 105162.
DOI URL |
| [10] |
CAI Y Y, MA L W, XI X L, et al. Comprehensive recovery of metals in spent Ni-Mo/γ-Al2O3 hydrofining catalyst. Hydrometallurgy, 2022, 208: 105800.
DOI URL |
| [11] |
CHEN B X, DU H, GUO Y N, et al. Recovering valuable metals from spent hydrodesulfurization catalysts by co-leaching, dissociation, and stepwise precipitation. Journal of Environmental Chemical Engineering, 2023, 11(2): 109365.
DOI URL |
| [12] |
LI H L, FENG Y L, WANG H J, et al. Separation of V (V) and Mo (VI) in roasting-water leaching solution of spent hydrodesulfurization catalyst by co-extraction using P 507 - N235 extractant. Separation and Purification Technology, 2020, 248: 117135.
DOI URL |
| [13] |
KAR B B. Carbothermic reduction of hydro-refining spent catalyst to extract molybdenum. International Journal of Mineral Processing, 2005, 75(3/4): 249.
DOI URL |
| [14] |
PARK K H, MOHAPATRA D, REDDY B R. Selective recovery of molybdenum from spent HDS catalyst using oxidative soda ash leach/carbon adsorption method. Journal of Hazardous Materials, 2006, 138(2): 311.
PMID |
| [15] |
ARSLANOĞLU H. Selective recovery of molybdenum from petroleum industry waste spent hydrodesulfurization Mo-Co-Ni/ Al2O3 catalyst in the presence of ammonia: process optimization and kinetic studies. Petroleum Chemistry, 2021, 61(2): 198.
DOI |
| [16] |
CHEN B X, DU H, WANG J Z, et al. A novel method to leach vanadium, molybdenum and nickel from spent hydrodesulfurization catalysts using hydroxyl radicals (HO•) in Fe2O3-assisted oxygen microbubble process. Hydrometallurgy, 2024, 223: 106225.
DOI URL |
| [17] |
CHEN R R, FENG C L, TAN J, et al. Stepwise separation and recovery of molybdenum, vanadium, and nickel from spent hydrogenation catalyst. Hydrometallurgy, 2022, 213: 105910.
DOI URL |
| [18] |
CHEN Y, FENG Q M, SHAO Y H, et al. Investigations on the extraction of molybdenum and vanadium from ammonia leaching residue of spent catalyst. International Journal of Mineral Processing, 2006, 79(1): 42.
DOI URL |
| [19] |
GAO B Y, JIANG H H, ZENG M, et al. High-efficiency recycling method for Mo and Ni from spent catalyst via soda roasting and solvent extraction. Journal of Cleaner Production, 2022, 367: 132976.
DOI URL |
| [20] | 孙晓雪, 王德举, 王宁, 等. 碱性水热法浸出处理废弃钴钼加氢催化剂. 化学反应工程与工艺, 2023, 39(2): 126. |
| [21] |
FENG C L, ZHANG C, YUAN S H, et al. Sustainable recovery of surface-deposited oils and valuable metals from uncrushed spent hydroprocessing catalysts. Journal of Cleaner Production, 2022, 338: 130564.
DOI URL |
| [22] |
ZHOU C J, SU J, JIANG X H, et al. Numerical simulation and experimental verification for the sorting behaviors of mixed biomass particles in a novel Z-shaped fluidized bed. Chemical Engineering Journal, 2022, 441: 136109.
DOI URL |
| [23] |
LU S, LAN B, XU J, et al. Optimization of multiple-chamber fluidized beds using coarse-grained CFD-DEM simulations: regulation of solids back-mixing. Powder Technology, 2023, 428: 118886.
DOI URL |
| [24] |
WANG T, WANG P, YIN Z Y, et al. Hydro-mechanical analysis of particle migration in fractures with CFD-DEM. Engineering Geology, 2024, 335: 107557.
DOI URL |
| [25] |
ELASWAD R, EL-SHEIMY N, MOHAMAD A. Trajectory dynamics of particles in accelerated toroidal pipe: a computational study using CFD-DPM simulations. Journal of Computational Science, 2024, 78: 102285.
DOI URL |
| [26] |
BAI W, KELLER N K G, HEINDEL T J, et al. Numerical study of mixing and segregation in a biomass fluidized bed. Powder Technology, 2013, 237: 355.
DOI URL |
| [27] |
WANG S, SHEN Y S. CFD-DEM study of biomass gasification in a fluidized bed reactor: effects of key operating parameters. Renewable Energy, 2020, 159: 1146.
DOI URL |
| [28] |
KAZEMI S, ZARGHAMI R, MOSTOUFI N, et al. CFD-DEM mixing of rod-like and spherical particles in fluidized beds. Powder Technology, 2024, 442: 119847.
DOI URL |
| [29] |
HE L P, LIU Z X, ZHAO Y Z. Study on a semi-resolved CFD-DEM method for rod-like particles in a gas-solid fluidized bed. Particuology, 2024, 87: 20.
DOI URL |
| [30] |
ZHAO L J, TAN Z, ZHANG X G, et al. Study on fluidized roasting of spent hydrodesulphurisation catalysts in large-scale industrial boiling furnace by CFD simulation. Energy, 2024, 302: 131818.
DOI URL |
| [31] |
LEE S J, AHN H S, LEE J H, et al. Granule efficiency evaluation process using two-way CFD-DEM coupling analysis. Chemical Engineering Journal, 2024, 498: 155123.
DOI URL |
| [32] |
XIE Z Z, SHEN Y S, TAKABATAKE K, et al. Coarse-grained DEM study of solids sedimentation in water. Powder Technology, 2020, 361: 21.
DOI URL |
| [33] |
YANG X L, WANG S B, YANG J T, et al. Study on heterogeneous gas-solid structure and interparticle collision behavior in a vibrated fluidized bed of Geldart D particles using CFD-DEM simulations. Powder Technology, 2023, 427: 118691.
DOI URL |
| [34] |
ZHU L T, HE J F, YANG B. Ultrasound-enhanced separation characteristics of gas-solid fluidized bed for fine-grained fluorite ore. Advanced Powder Technology, 2024, 35(1): 104293.
DOI URL |
| [35] |
PINHEIRO D R, DE F NEVES R, PAZ S P A. A sequential Box-Behnken design (BBD) and response surface methodology (RSM) to optimize SAPO-34 synthesis from Kaolin waste. Microporous and Mesoporous Materials, 2021, 323: 111250.
DOI URL |
| [36] |
ARABKHANI P, ASFARAM A, ATEIA M. Easy-to-prepare graphene oxide/sodium montmorillonite polymer nanocomposite with enhanced adsorption performance. Journal of Water Process Engineering, 2020, 38: 101651.
DOI URL |
| [37] |
BAGHERI R, GHAEDI M, ASFARAM A, et al. RSM-CCD design of malachite green adsorption onto activated carbon with multimodal pore size distribution prepared from Amygdalus scoparia: kinetic and isotherm studies. Polyhedron, 2019, 171: 464.
DOI URL |
| [38] |
CHEN A R, WANG S X, ZHANG L B, et al. Optimization of the microwave roasting extraction of palladium and rhodium from spent automobile catalysts using response surface analysis. International Journal of Mineral Processing, 2015, 143: 18.
DOI URL |
| [39] |
CHEN Z Y, NIU B, ZHANG L G, et al. Vacuum pyrolysis characteristics and parameter optimization of recycling organic materials from waste tantalum capacitors. Journal of Hazardous Materials, 2018, 342: 192.
DOI PMID |
| [40] |
YUAN Y Z, ZHANG Y M, LIU T, et al. Optimization of microwave roasting-acid leaching process for vanadium extraction from shale via response surface methodology. Journal of Cleaner Production, 2019, 234: 494.
DOI URL |
| [1] | SHI Yanlei, SUN Niefeng, XU Chengyan, WANG Shujie, LIN Peng, MA Chunlei, XU Senfeng, WANG Wei, CHEN Chunmei, FU Lijie, SHAO Huimin, LI Xiaolan, WANG Yang, QIN Jingkai. Thermal Field of 6-inch Indium Phosphide Single Crystal Growth by Semi-sealed Czochralski Method [J]. Journal of Inorganic Materials, 2023, 38(3): 335-342. |
| [2] | MU Honghe, WANG Pengfei, SHI Yufeng, ZHANG Zhonghan, WU Anhua, SU Liangbi. Large-size CeF3 Crystal Growth by Heat Exchanger-Bridgman Method: Thermal Field Design and Optimization [J]. Journal of Inorganic Materials, 2023, 38(3): 288-295. |
| [3] | GENG Rui-Wen, YANG Xiao-Jing, XIE Qi-Ming, LI Rui, LUO Liang. Material Removal Mechanism of Monocrystalline Germanium Based on Nano-scratch Experiment [J]. Journal of Inorganic Materials, 2019, 34(8): 867-872. |
| [4] | CHEN Wen-Bo, CHEN Lun-Jiang, LIU Chuan-Dong, CHENG Chang-Ming, TONG Hong-Hui, ZHU Hai-Long. Preparation of Spherical Alumina Powder by RF Thermal Plasma: Numerical Simulation and Experimentation [J]. Journal of Inorganic Materials, 2018, 33(5): 550-556. |
| [5] | WANG Xiao-Yuan, YAN Ya-Bin, SHIMADA Takahiro, KITAMURA Takayuki. Research Progress in Atomistic Simulation on Ferroelectricity and Electromechanical Coupling Behavior of Nanoscale Ferroelectrics [J]. Journal of Inorganic Materials, 2015, 30(6): 561-570. |
| [6] | LIU Guang-Xia, WANG Sheng-Lai, DING Jian-Xu, SUN Yun, LIU Wen-Jie, ZHU Sheng-Jun. Numerical Simulation of the Influence of Different Rotation Speeds on the Capping of KDP Crystal [J]. Journal of Inorganic Materials, 2013, 28(06): 665-670. |
| [7] | WANG Wei-Qing,FENG Qi-Ming,DONG Fa-Qin,LI Hu-Jie,ZHAO Xiao-Dong. Preparation and Properties of Fe3O4/Clinoptilolite Magnetic Composite [J]. Journal of Inorganic Materials, 2010, 25(4): 401-405. |
| [8] |
WEI Xi,CHENG Lai-Fei,ZHANG Li-Tong,XU Yong-Dong.
Numerical Simulation of Isothermal Chemical Vapor Infiltration Process for Fabrication of C/SiC Composites [J]. Journal of Inorganic Materials, 2006, 21(5): 1179-1184. |
| [9] | CHANG Xu,TANG Chun-An,ZHANG Hou-Quan,ZHANG Yong-Bin,ZHANG Ya-Fang. Numerical Approach to Toughening Design of Laminated Ceramic Composites [J]. Journal of Inorganic Materials, 2005, 20(2): 459-464. |
| [10] | YU Hui-Ping,SUI Yun-Kang,ZHANG Feng-Yi,CHANG Xin-An,AN Guo-Ping. Numerical Simulation of a Czochralski Silicon Crystal Growth with a Large Diameter 300mm Under a Cusp Magnetic Field [J]. Journal of Inorganic Materials, 2005, 20(2): 453-458. |
| [11] | LIU Zhao-Hua,JIN Wei-Qing,PAN Zhi-Lei,LIANG Xin-An,CHEN Gang-Yi. Experiment and Numerical Simulation of Velocity and Temperature Fields in KNbO3 Solution [J]. Journal of Inorganic Materials, 2002, 17(6): 1112-1116. |
| [12] | ZHANG Hai-Bin,SHEN Ding-Zhong,REN Guo-Hao,GONG Bo. Research Progress on the Numerical Simulation of Transport Process in Vertical Bridgman Crystal Growth [J]. Journal of Inorganic Materials, 2002, 17(5): 910-914. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||