无机材料学报 ›› 2025, Vol. 40 ›› Issue (12): 1387-1394.DOI: 10.15541/jim20250027 CSTR: 32189.14.jim20250027
赵丽娟1,2( ), 谭哲1,2, 张晓光1,2(
), 谭哲1,2, 张晓光1,2( ), 蒋国赛1,2, 陶然1,2, 潘德安2,3,4(
), 蒋国赛1,2, 陶然1,2, 潘德安2,3,4( )
)
收稿日期:2025-01-18
修回日期:2025-04-15
出版日期:2025-12-20
网络出版日期:2025-05-09
通讯作者:
张晓光, 研究员. E-mail: zhangxg@bjut.edu.cn;作者简介:赵丽娟(1997-), 女, 博士研究生. E-mail: zhaolijuan97@163.com
基金资助:
ZHAO Lijuan1,2( ), TAN Zhe1,2, ZHANG Xiaoguang1,2(
), TAN Zhe1,2, ZHANG Xiaoguang1,2( ), JIANG Guosai1,2, TAO Ran1,2, PAN De’an2,3,4(
), JIANG Guosai1,2, TAO Ran1,2, PAN De’an2,3,4( )
)
Received:2025-01-18
Revised:2025-04-15
Published:2025-12-20
Online:2025-05-09
Contact:
ZHANG Xiaoguang, professor. E-mail: zhangxg@bjut.edu.cn;About author:ZHAO Lijuan (1997-), female, PhD candidate. E-mail: zhaolijuan97@163.com
Supported by:摘要:
废加氢催化剂具有报废量大、颗粒完整度高等特性, 是再生催化剂载体的重要来源。现有废加氢催化剂回收技术大多关注其中的有价金属, 对于载体颗粒的回收研究较少。本研究针对条状废加氢催化剂颗粒难以通过传统筛分实现有效分级的关键问题, 创新性地提出采用流化床进行颗粒分级的策略。采用计算流体动力学(CFD)和离散单元模型(DEM)耦合模拟的研究方法, 结合响应面法(RSM)系统揭示了流化床分级的内在机理及工艺优化规律。研究表明, 流化床通过气固两相流态化作用可实现不同长径比颗粒的高效分级, 气体速度对分级效率的影响最为显著, 其次是进料流量, 进料口高度的影响相对较小。在一定的气体速度和进料口高度下, 存在进料流量阈值, 超过此值分级效率将会下降。通过建立Box-Behnken设计(BBD)模型, 确定当气体速度为10.45 m/s, 进料流量为7.50 t/h, 进料口高度为3.50 m时, 分级效率达到100%。本研究阐明了流化床分级过程的多物理场耦合机制, 为废加氢催化剂回收过程中的载体颗粒预分级工艺提供了理论参考。
中图分类号:
赵丽娟, 谭哲, 张晓光, 蒋国赛, 陶然, 潘德安. 废加氢催化剂颗粒分级数值模拟研究[J]. 无机材料学报, 2025, 40(12): 1387-1394.
ZHAO Lijuan, TAN Zhe, ZHANG Xiaoguang, JIANG Guosai, TAO Ran, PAN De’an. Numerical Simulation of Particle Classification for Spent Hydrogenation Catalyst[J]. Journal of Inorganic Materials, 2025, 40(12): 1387-1394.

图2 (a1, b1)理论推导与(a2, b2)模拟仿真结果分析
Fig. 2 Analysis of (a1, b1) theoretical derivation and (a2, b2) simulation (a1, a2) dp=0.29 mm; (b1, b2) dp=2.19 mm. Colorful figures are available on website

图4 (a1, a2)气体速度、(b1, b2)进料口高度和(c1, c2)进料流量对(a1, b1, c1)分级效率以及(a2, b2, c2)产品收集区最小粒径的影响
Fig. 4 Effects of (a1, a2) gas velocity, (b1, b2) inlet height, and (c1, c2) feed flow on (a1, b1, c1) grading efficiency and (a2, b2, c2) minimum particle diameter in the product collection section Colorful figures are available on website

图5 模型残差分析
Fig. 5 Model residual analysis (a) Normal probability versus externally studentized residual; (b) Externally studentized residual versus predicted value; (c) Externally studentized residual versus run number; (d) Predicted value versus actual value. Colorful figures are available on website
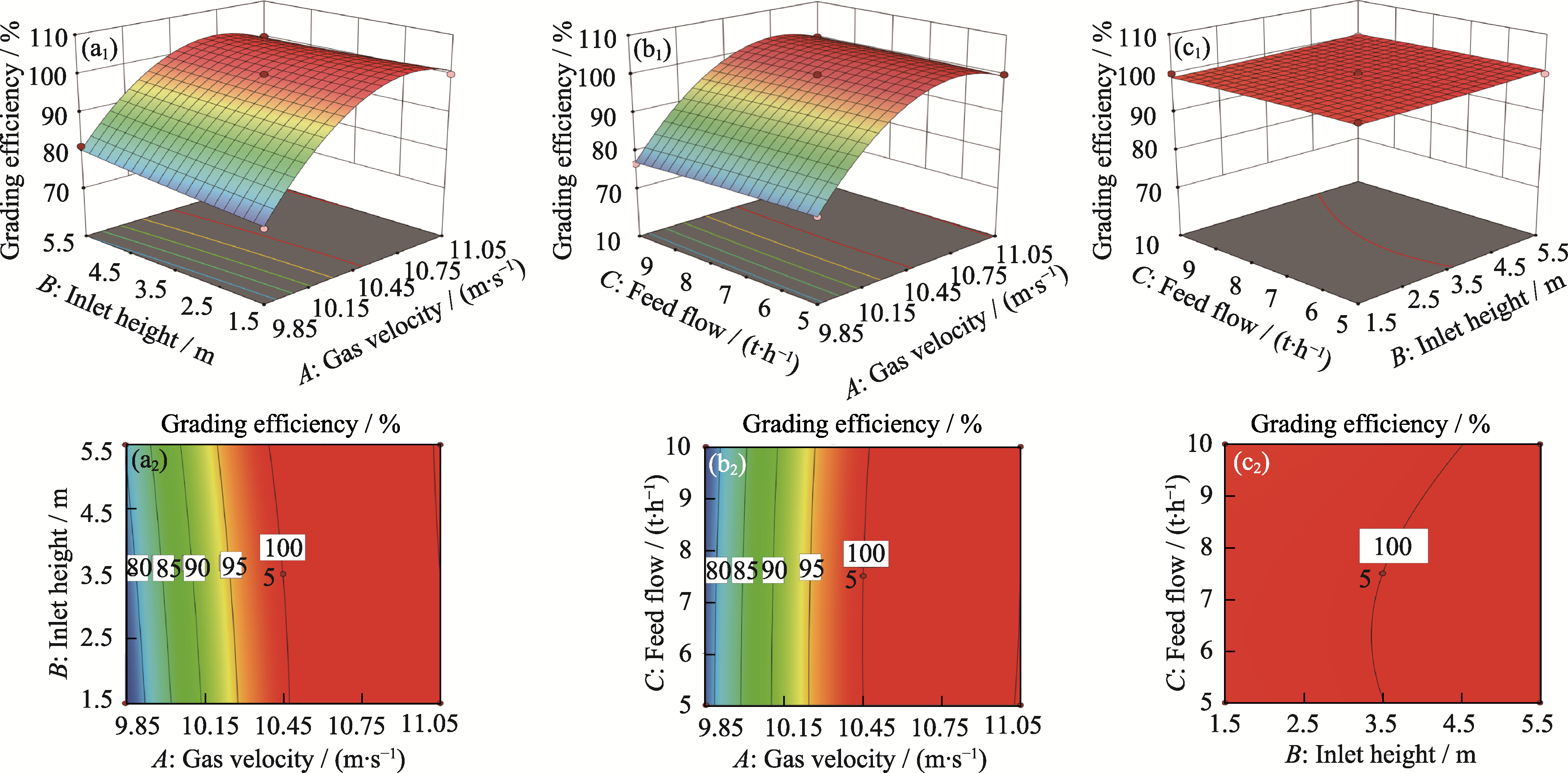
图6 响应面分析
Fig. 6 Response surface analysis (a1, a2) Factors gas velocity A and inlet height B; (b1, b2) Factors gas velocity A and feed flow C; (c1, c2) Factors inlet height B and feed flow C;(a1, b1, c1) Response surface; (a2, b2, c2) Contour plots. Colorful figures are available on website
| Average mass conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=0$ |
|---|
| Average momentum conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=-\alpha_{\mathrm{g}} \nabla P+\nabla \cdot\left(\alpha_{\mathrm{g}} \tau_{\mathrm{g}}\right)+F_{\mathrm{p} \rightarrow \mathrm{~g}}+\alpha_{\mathrm{g}} \rho_{\mathrm{g}} g$ |
| Velocity vector of the gas phase: $\tau_{\mathrm{g}}=\mu_{\mathrm{g}}\left(\nabla \boldsymbol{v}_{\mathrm{g}}+\nabla \boldsymbol{v}_{\mathrm{g}}^{T}\right)-2 / 3 \cdot\left(\nabla \boldsymbol{v}_{\mathrm{g}}\right) \boldsymbol{I}$ |
| Gas phase density: $\rho_{\mathrm{g}}=P_{\mathrm{g}} M / R_{\mathrm{g}} T$ |
| Momentum source term interacting with the particle phase: $F_{\mathrm{p} \rightarrow \mathrm{~g}}=-\sum_{p=1}^{n} F_{\mathrm{g} \rightarrow \mathrm{p}} / V_{\mathrm{C}}$ |
| Force generated by the gas phase on the particles: $F_{\mathrm{g} \rightarrow \mathrm{p}}=F_{\mathrm{D}}+F_{\nabla P}$ |
| Pressure gradient force $F_{\nabla P}$: $F_{\nabla P}=-V_{\mathrm{p}} \nabla P$ |
| Drag force calculation when using CGM: $F_{\mathrm{D}, \mathrm{CGM}}=1 / 2 \cdot\left(f_{\mathrm{CGM}}^{3} C_{\mathrm{D}} \rho_{\mathrm{g}} A^{\prime}\left|\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right|\left(\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right)\right)$ |
| Where $C_{D}$ is the drag coefficient, expressed as: $C_{\mathrm{D}}=\psi C_{\mathrm{D} 1}+(1-\psi) C_{\mathrm{D} 2}$ |
| Where $\psi$ is the mixing parameter, calculated by: $\psi=1 / \pi \cdot \tan ^{-1}\left[150 \cdot 1.75\left(0.8-\alpha_{\mathrm{g}}\right)\right]+0.5$ |
| Where $C_{\mathrm{D} 1}$ is expressed as: $C_{\mathrm{D} 1}=200 \alpha_{\mathrm{p}} / \alpha_{\mathrm{g}} \phi^{2} R e+7 / 3 \phi$ |
| Where $\psi$ is the sphericity of the particles, defined as: $\phi=A_{\mathrm{sph}} / A_{\mathrm{p}}$ |
| Where $C_{\mathrm{D} 2}$ is expressed as: $C_{\mathrm{D} 2}=\alpha_{\mathrm{g}}^{-1.65} \max \left\{24 / \alpha_{\mathrm{g}} R e_{\mathrm{p}} \cdot\left[1+0.15\left(\alpha_{\mathrm{g}} R e_{\mathrm{p}}\right)^{0.687}\right], 0.44\right\}$ |
| Particle relative Reynolds number $R e_{\mathrm{p}}$ when using CGM: $R e_{\mathrm{p}, \mathrm{CGM}}=\rho_{\mathrm{g}}\left|\boldsymbol{v}_{\mathrm{p}}-\boldsymbol{v}_{\mathrm{g}}\right| d_{\mathrm{p}, \mathrm{CGM}} / f_{\mathrm{CGM}} \mu_{\mathrm{g}}$ |
表S1 粗粒化CFD-DEM方法中的主要方程
Table S1 Main equations in coarse-grained CFD-DEM method
| Average mass conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=0$ |
|---|
| Average momentum conservation equation: $\partial\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right) / \partial t+\nabla \cdot\left(\alpha_{\mathrm{g}} \rho_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}} \boldsymbol{v}_{\mathrm{g}}\right)=-\alpha_{\mathrm{g}} \nabla P+\nabla \cdot\left(\alpha_{\mathrm{g}} \tau_{\mathrm{g}}\right)+F_{\mathrm{p} \rightarrow \mathrm{~g}}+\alpha_{\mathrm{g}} \rho_{\mathrm{g}} g$ |
| Velocity vector of the gas phase: $\tau_{\mathrm{g}}=\mu_{\mathrm{g}}\left(\nabla \boldsymbol{v}_{\mathrm{g}}+\nabla \boldsymbol{v}_{\mathrm{g}}^{T}\right)-2 / 3 \cdot\left(\nabla \boldsymbol{v}_{\mathrm{g}}\right) \boldsymbol{I}$ |
| Gas phase density: $\rho_{\mathrm{g}}=P_{\mathrm{g}} M / R_{\mathrm{g}} T$ |
| Momentum source term interacting with the particle phase: $F_{\mathrm{p} \rightarrow \mathrm{~g}}=-\sum_{p=1}^{n} F_{\mathrm{g} \rightarrow \mathrm{p}} / V_{\mathrm{C}}$ |
| Force generated by the gas phase on the particles: $F_{\mathrm{g} \rightarrow \mathrm{p}}=F_{\mathrm{D}}+F_{\nabla P}$ |
| Pressure gradient force $F_{\nabla P}$: $F_{\nabla P}=-V_{\mathrm{p}} \nabla P$ |
| Drag force calculation when using CGM: $F_{\mathrm{D}, \mathrm{CGM}}=1 / 2 \cdot\left(f_{\mathrm{CGM}}^{3} C_{\mathrm{D}} \rho_{\mathrm{g}} A^{\prime}\left|\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right|\left(\boldsymbol{v}_{\mathrm{g}}-\boldsymbol{v}_{\mathrm{p}}\right)\right)$ |
| Where $C_{D}$ is the drag coefficient, expressed as: $C_{\mathrm{D}}=\psi C_{\mathrm{D} 1}+(1-\psi) C_{\mathrm{D} 2}$ |
| Where $\psi$ is the mixing parameter, calculated by: $\psi=1 / \pi \cdot \tan ^{-1}\left[150 \cdot 1.75\left(0.8-\alpha_{\mathrm{g}}\right)\right]+0.5$ |
| Where $C_{\mathrm{D} 1}$ is expressed as: $C_{\mathrm{D} 1}=200 \alpha_{\mathrm{p}} / \alpha_{\mathrm{g}} \phi^{2} R e+7 / 3 \phi$ |
| Where $\psi$ is the sphericity of the particles, defined as: $\phi=A_{\mathrm{sph}} / A_{\mathrm{p}}$ |
| Where $C_{\mathrm{D} 2}$ is expressed as: $C_{\mathrm{D} 2}=\alpha_{\mathrm{g}}^{-1.65} \max \left\{24 / \alpha_{\mathrm{g}} R e_{\mathrm{p}} \cdot\left[1+0.15\left(\alpha_{\mathrm{g}} R e_{\mathrm{p}}\right)^{0.687}\right], 0.44\right\}$ |
| Particle relative Reynolds number $R e_{\mathrm{p}}$ when using CGM: $R e_{\mathrm{p}, \mathrm{CGM}}=\rho_{\mathrm{g}}\left|\boldsymbol{v}_{\mathrm{p}}-\boldsymbol{v}_{\mathrm{g}}\right| d_{\mathrm{p}, \mathrm{CGM}} / f_{\mathrm{CGM}} \mu_{\mathrm{g}}$ |
| Symbol | Physical significance |
|---|---|
| $g$ | Gas phase |
| $p$ | Particle phase |
| $\alpha_{\mathrm{p}}$ | Concentration of the particulate phase |
| $\rho_{\mathrm{g}}$ | Density of the gas phase |
| $\rho_{\mathrm{p}}$ | Density of the particulate phase |
| $V_{\mathrm{g}}$ | Velocity vector of the gas phase |
| $V_{\mathrm{p}}$ | Velocity vector of the particulate phase |
| $\tau_{\mathrm{g}}$ | Viscous stress tensor of the gas phase |
| $T$ | Temperature of the gas phase |
| $I$ | Identity matrix |
| $P_{g}$ | Pressure of the gas |
| $n$ | Number of particles inside the computational cell volume |
| $V_{C}$ | Computational cell volume |
| $F_{\mathrm{p} \rightarrow \mathrm{~g}}$ | Force generated by the particles on the gas phase |
| F_{\mathrm{g} \rightarrow \mathrm{~p}} | Force generated by the gas phase on the particulate phase |
| $F_{D}$ | Drag force |
| $F_{\nabla P}$ | Pressure gradient force |
| $V_{p}$ | Volume of the particle |
| $\nabla p$ | Local pressure gradient |
| $A'$ | Projected particle area in the flow direction |
| $f_{\mathrm{CGM}}$ | Scale factor of the coarse particle |
| $f_{\mathrm{D,CGM}}$ | Drag force of the coarse particle |
| $C_{D}$ | Drag coefficient |
| $\psi$ | Mixing parameter |
| $\phi$ | Sphericity of the particles |
| $A_{sph}$ | Surface area of a sphere with the same volume as the particle |
| $A_{p}$ | Actual surface area of the particle |
| $R e_{\mathrm{p}, \mathrm{CGM}}$ | Particle relative Reynolds number of the coarse particle |
| $d_{\mathrm{p}, \mathrm{CGM}}$ | Diameter of the coarse particle |
| $\mu_{\mathrm{g}}$ | Viscosity of gas phase |
| $d_{p}$ | Spherical equivalent diameter of the particle |
| $V_{HDS}$ | Volume of the spent hydrogenation (HDS) catalyst rod particle |
| $t$ | Graded time of the spent HDS catalyst particles |
| $G$ | Gravity of the spent HDS catalyst particles |
| $m$ | Mass of the spent HDS catalyst particles |
| $g$ | Acceleration due to gravity |
| $α$ | Acceleration of the particle |
| $V_{pi}$ | Velocity of a particle dropped from the inlet at i second |
| $V_{gi}$ | Cross-sectional gas velocity at i second |
| $α_{i}$ | Acceleration of a particle dropped from the inlet at i second |
| $L_{i}$ | Distance of a particle dropped from the inlet at i second |
| $\lambda$ | Gradation efficiency |
| $N_{1}$ | Number of the spent HDS catalyst particles with a diameter greater than 1.5 mm in the product collection section |
| $N_{2}$ | Total number of spent HDS catalyst particles in the product collection section |
表S2 符号命名
Table S2 Nomenclature of the symbols
| Symbol | Physical significance |
|---|---|
| $g$ | Gas phase |
| $p$ | Particle phase |
| $\alpha_{\mathrm{p}}$ | Concentration of the particulate phase |
| $\rho_{\mathrm{g}}$ | Density of the gas phase |
| $\rho_{\mathrm{p}}$ | Density of the particulate phase |
| $V_{\mathrm{g}}$ | Velocity vector of the gas phase |
| $V_{\mathrm{p}}$ | Velocity vector of the particulate phase |
| $\tau_{\mathrm{g}}$ | Viscous stress tensor of the gas phase |
| $T$ | Temperature of the gas phase |
| $I$ | Identity matrix |
| $P_{g}$ | Pressure of the gas |
| $n$ | Number of particles inside the computational cell volume |
| $V_{C}$ | Computational cell volume |
| $F_{\mathrm{p} \rightarrow \mathrm{~g}}$ | Force generated by the particles on the gas phase |
| F_{\mathrm{g} \rightarrow \mathrm{~p}} | Force generated by the gas phase on the particulate phase |
| $F_{D}$ | Drag force |
| $F_{\nabla P}$ | Pressure gradient force |
| $V_{p}$ | Volume of the particle |
| $\nabla p$ | Local pressure gradient |
| $A'$ | Projected particle area in the flow direction |
| $f_{\mathrm{CGM}}$ | Scale factor of the coarse particle |
| $f_{\mathrm{D,CGM}}$ | Drag force of the coarse particle |
| $C_{D}$ | Drag coefficient |
| $\psi$ | Mixing parameter |
| $\phi$ | Sphericity of the particles |
| $A_{sph}$ | Surface area of a sphere with the same volume as the particle |
| $A_{p}$ | Actual surface area of the particle |
| $R e_{\mathrm{p}, \mathrm{CGM}}$ | Particle relative Reynolds number of the coarse particle |
| $d_{\mathrm{p}, \mathrm{CGM}}$ | Diameter of the coarse particle |
| $\mu_{\mathrm{g}}$ | Viscosity of gas phase |
| $d_{p}$ | Spherical equivalent diameter of the particle |
| $V_{HDS}$ | Volume of the spent hydrogenation (HDS) catalyst rod particle |
| $t$ | Graded time of the spent HDS catalyst particles |
| $G$ | Gravity of the spent HDS catalyst particles |
| $m$ | Mass of the spent HDS catalyst particles |
| $g$ | Acceleration due to gravity |
| $α$ | Acceleration of the particle |
| $V_{pi}$ | Velocity of a particle dropped from the inlet at i second |
| $V_{gi}$ | Cross-sectional gas velocity at i second |
| $α_{i}$ | Acceleration of a particle dropped from the inlet at i second |
| $L_{i}$ | Distance of a particle dropped from the inlet at i second |
| $\lambda$ | Gradation efficiency |
| $N_{1}$ | Number of the spent HDS catalyst particles with a diameter greater than 1.5 mm in the product collection section |
| $N_{2}$ | Total number of spent HDS catalyst particles in the product collection section |
| Diameter/mm | Percentage/% |
|---|---|
| 0.29 | 1.00 |
| 1.14 | 3.04 |
| 1.44 | 35.50 |
| 1.65 | 34.28 |
| 1.82 | 14.81 |
| 1.96 | 6.03 |
| 2.08 | 3.45 |
| 2.19 | 1.89 |
表S3 颗粒的组成
Table S3 Composition of particles
| Diameter/mm | Percentage/% |
|---|---|
| 0.29 | 1.00 |
| 1.14 | 3.04 |
| 1.44 | 35.50 |
| 1.65 | 34.28 |
| 1.82 | 14.81 |
| 1.96 | 6.03 |
| 2.08 | 3.45 |
| 2.19 | 1.89 |
| Diameter/mm | Velocity/(m·s-1) |
|---|---|
| 1.14 | 8.23 |
| 1.44 | 9.25 |
| 1.65 | 9.90 |
| 1.82 | 10.39 |
| 1.96 | 10.79 |
| 2.08 | 11.11 |
| 2.19 | 11.40 |
表S4 颗粒分级所需的临界气体速度
Table S4 Critical gas velocity required for particle gradation
| Diameter/mm | Velocity/(m·s-1) |
|---|---|
| 1.14 | 8.23 |
| 1.44 | 9.25 |
| 1.65 | 9.90 |
| 1.82 | 10.39 |
| 1.96 | 10.79 |
| 2.08 | 11.11 |
| 2.19 | 11.40 |
| Physical property | Value |
|---|---|
| fCGM | 7 |
| Particle temperature | 300 K |
| Gas velocity | 9.25 m/s |
| Feed flow | 1.25 t /h |
| Inlet height | 3.50 m |
表S5 流化床模型验证的边界条件
Table S5 Boundary conditions of model validation for the fluidized graded bed
| Physical property | Value |
|---|---|
| fCGM | 7 |
| Particle temperature | 300 K |
| Gas velocity | 9.25 m/s |
| Feed flow | 1.25 t /h |
| Inlet height | 3.50 m |
| Independent variable | Unit | Symbol | Factor level | ||
|---|---|---|---|---|---|
| -1 | 0 | -1 | |||
| Gas velocity | m/s | A | 9.85 | 10.45 | 11.05 |
| Inlet height | m | B | 1.5 | 3.5 | 5.5 |
| Feed flow | t/h | C | 5 | 7.5 | 10 |
表S6 BBD的三因素三水平设计
Table S6 Three-factor and three-level for BBD
| Independent variable | Unit | Symbol | Factor level | ||
|---|---|---|---|---|---|
| -1 | 0 | -1 | |||
| Gas velocity | m/s | A | 9.85 | 10.45 | 11.05 |
| Inlet height | m | B | 1.5 | 3.5 | 5.5 |
| Feed flow | t/h | C | 5 | 7.5 | 10 |
| NO. | Independent variable | Response value | ||
|---|---|---|---|---|
| Gas velocity, A/(m·s-1) | Inlet height, B/m | Feed flow, C/(t·h-1) | Grading efficiency, $\lambda$/% | |
| 1 | 10.45 | 3.5 | 7.5 | 100 |
| 2 | 9.85 | 1.5 | 7.5 | 75.37 |
| 3 | 11.05 | 5.5 | 7.5 | 100 |
| 4 | 10.45 | 3.5 | 7.5 | 100 |
| 5 | 10.45 | 3.5 | 7.5 | 100 |
| 6 | 11.05 | 3.5 | 10 | 100 |
| 7 | 10.45 | 5.5 | 10 | 100 |
| 8 | 9.85 | 3.5 | 10 | 76.56 |
| 9 | 10.45 | 1.5 | 10 | 100 |
| 10 | 10.45 | 3.5 | 7.5 | 100 |
| 11 | 10.45 | 5.5 | 5 | 100 |
| 12 | 9.85 | 5.5 | 7.5 | 81.17 |
| 13 | 10.45 | 1.5 | 5 | 100 |
| 14 | 11.05 | 3.5 | 5 | 100 |
| 15 | 9.85 | 3.5 | 5 | 78.24 |
| 16 | 10.45 | 3.5 | 7.5 | 100 |
| 17 | 11.05 | 1.5 | 7.5 | 100 |
表S7 分级效率的RSM设计与仿真结果
Table S7 Design and simulation results of RSM of grading efficiency
| NO. | Independent variable | Response value | ||
|---|---|---|---|---|
| Gas velocity, A/(m·s-1) | Inlet height, B/m | Feed flow, C/(t·h-1) | Grading efficiency, $\lambda$/% | |
| 1 | 10.45 | 3.5 | 7.5 | 100 |
| 2 | 9.85 | 1.5 | 7.5 | 75.37 |
| 3 | 11.05 | 5.5 | 7.5 | 100 |
| 4 | 10.45 | 3.5 | 7.5 | 100 |
| 5 | 10.45 | 3.5 | 7.5 | 100 |
| 6 | 11.05 | 3.5 | 10 | 100 |
| 7 | 10.45 | 5.5 | 10 | 100 |
| 8 | 9.85 | 3.5 | 10 | 76.56 |
| 9 | 10.45 | 1.5 | 10 | 100 |
| 10 | 10.45 | 3.5 | 7.5 | 100 |
| 11 | 10.45 | 5.5 | 5 | 100 |
| 12 | 9.85 | 5.5 | 7.5 | 81.17 |
| 13 | 10.45 | 1.5 | 5 | 100 |
| 14 | 11.05 | 3.5 | 5 | 100 |
| 15 | 9.85 | 3.5 | 5 | 78.24 |
| 16 | 10.45 | 3.5 | 7.5 | 100 |
| 17 | 11.05 | 1.5 | 7.5 | 100 |
| Standard deviation | Mean | Coefficient of variance/% | R2 | Adj. R2 | Pred. R2 | Adeq Precision |
|---|---|---|---|---|---|---|
| 0.8397 | 94.78 | 0.8860 | 0.9968 | 0.9926 | 0.9481 | 38.9173 |
表S8 模型拟合
Table S8 Model fit statistics
| Standard deviation | Mean | Coefficient of variance/% | R2 | Adj. R2 | Pred. R2 | Adeq Precision |
|---|---|---|---|---|---|---|
| 0.8397 | 94.78 | 0.8860 | 0.9968 | 0.9926 | 0.9481 | 38.9173 |
| Source | Coefficient estimate | Sum of squares | Degree of freedom | Mean square | F value | P value |
|---|---|---|---|---|---|---|
| Model | - | 1516.81 | 9 | 168.53 | 239.00 | <0.0001 |
| A | 11.0825 | 982.57 | 1 | 982.57 | 1393.37 | <0.0001 |
| B | 0.725 | 4.21 | 1 | 4.21 | 5.96 | 0.0446 |
| C | -0.21 | 0.3528 | 1 | 0.3528 | 0.5003 | 0.5022 |
| AB | -1.45 | 8.41 | 1 | 8.41 | 11.93 | 0.0106 |
| AC | 0.42 | 0.7056 | 1 | 0.7056 | 1 | 0.3505 |
| BC | -8.71×10-16 | 0 | 1 | 0 | 0 | 1 |
| A2 | -11.0825 | 517.14 | 1 | 517.14 | 733.35 | <0.0001 |
| B2 | 0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| C2 | -0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
表S9 回归方程方差
Table S9 ANOVA results of the regression equation
| Source | Coefficient estimate | Sum of squares | Degree of freedom | Mean square | F value | P value |
|---|---|---|---|---|---|---|
| Model | - | 1516.81 | 9 | 168.53 | 239.00 | <0.0001 |
| A | 11.0825 | 982.57 | 1 | 982.57 | 1393.37 | <0.0001 |
| B | 0.725 | 4.21 | 1 | 4.21 | 5.96 | 0.0446 |
| C | -0.21 | 0.3528 | 1 | 0.3528 | 0.5003 | 0.5022 |
| AB | -1.45 | 8.41 | 1 | 8.41 | 11.93 | 0.0106 |
| AC | 0.42 | 0.7056 | 1 | 0.7056 | 1 | 0.3505 |
| BC | -8.71×10-16 | 0 | 1 | 0 | 0 | 1 |
| A2 | -11.0825 | 517.14 | 1 | 517.14 | 733.35 | <0.0001 |
| B2 | 0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| C2 | -0.2175 | 0.1992 | 1 | 0.1992 | 0.2825 | 0.6115 |
| [1] |
TRAN T T, LEE M S. Separation of Mo(VI), V(V), Ni(II), Al(III) from synthetic hydrochloric acidic leaching solution of spent catalysts by solvent extraction with ionic liquid. Separation and Purification Technology, 2020, 247: 117005.
DOI URL |
| [2] |
VALVERDE I M, PAULINO J F, AFONSO J C. Hydrometallurgical route to recover molybdenum, nickel, cobalt and aluminum from spent hydrotreating catalysts in sulphuric acid medium. Journal of Hazardous Materials, 2008, 160(2/3): 310.
DOI PMID |
| [3] |
WANG W Q, ZHANG L, HAN Y, et al. Cleaner recycling of spent Ni-Mo/γ-Al2O3 catalyst based on mineral phase reconstruction. Journal of Cleaner Production, 2019, 232: 266.
DOI URL |
| [4] |
WANG J Z, WANG S N, OLAYIWOLA A, et al. Recovering valuable metals from spent hydrodesulfurization catalyst via blank roasting and alkaline leaching. Journal of Hazardous Materials, 2021, 416: 125849.
DOI URL |
| [5] |
LIANG X, TANG J J, LI L S, et al. A review of metallurgical processes and purification techniques for recovering Mo, V, Ni, Co, Al from spent catalysts. Journal of Cleaner Production, 2022, 376: 134108.
DOI URL |
| [6] | 窦中堃, 张家靓, 陈永强, 等. 废加氢催化剂熔炼合金酸浸液中钼、镍萃取分离研究. 有色金属科学与工程, 2024, 15(1): 1. |
| [7] | ARSLANOĞLU H, YARAŞ A. Recovery of molybdenum, cobalt and nickel from spent hydrodesulphurization catalyst through oxidizing roast followed by sodium persulfate leaching. Sustainable Materials and Technologies, 2021, 28: e00286. |
| [8] | BARIK S P, PARK K H, PARHI P K, et al. Direct leaching of molybdenum and cobalt from spent hydrodesulphurization catalyst with sulphuric acid. Hydrometallurgy, 2012, 111: 46. |
| [9] |
HE R Y, LI D, YANG K P, et al. Process optimization and modeling of recycling Mo (VI) from spent Mo-Fe2O3/Al2O3 catalyst by roasting with sodium carbonate using response surface methodology (RSM). International Journal of Refractory Metals and Hard Materials, 2020, 87: 105162.
DOI URL |
| [10] |
CAI Y Y, MA L W, XI X L, et al. Comprehensive recovery of metals in spent Ni-Mo/γ-Al2O3 hydrofining catalyst. Hydrometallurgy, 2022, 208: 105800.
DOI URL |
| [11] |
CHEN B X, DU H, GUO Y N, et al. Recovering valuable metals from spent hydrodesulfurization catalysts by co-leaching, dissociation, and stepwise precipitation. Journal of Environmental Chemical Engineering, 2023, 11(2): 109365.
DOI URL |
| [12] |
LI H L, FENG Y L, WANG H J, et al. Separation of V (V) and Mo (VI) in roasting-water leaching solution of spent hydrodesulfurization catalyst by co-extraction using P 507 - N235 extractant. Separation and Purification Technology, 2020, 248: 117135.
DOI URL |
| [13] |
KAR B B. Carbothermic reduction of hydro-refining spent catalyst to extract molybdenum. International Journal of Mineral Processing, 2005, 75(3/4): 249.
DOI URL |
| [14] |
PARK K H, MOHAPATRA D, REDDY B R. Selective recovery of molybdenum from spent HDS catalyst using oxidative soda ash leach/carbon adsorption method. Journal of Hazardous Materials, 2006, 138(2): 311.
PMID |
| [15] |
ARSLANOĞLU H. Selective recovery of molybdenum from petroleum industry waste spent hydrodesulfurization Mo-Co-Ni/ Al2O3 catalyst in the presence of ammonia: process optimization and kinetic studies. Petroleum Chemistry, 2021, 61(2): 198.
DOI |
| [16] |
CHEN B X, DU H, WANG J Z, et al. A novel method to leach vanadium, molybdenum and nickel from spent hydrodesulfurization catalysts using hydroxyl radicals (HO•) in Fe2O3-assisted oxygen microbubble process. Hydrometallurgy, 2024, 223: 106225.
DOI URL |
| [17] |
CHEN R R, FENG C L, TAN J, et al. Stepwise separation and recovery of molybdenum, vanadium, and nickel from spent hydrogenation catalyst. Hydrometallurgy, 2022, 213: 105910.
DOI URL |
| [18] |
CHEN Y, FENG Q M, SHAO Y H, et al. Investigations on the extraction of molybdenum and vanadium from ammonia leaching residue of spent catalyst. International Journal of Mineral Processing, 2006, 79(1): 42.
DOI URL |
| [19] |
GAO B Y, JIANG H H, ZENG M, et al. High-efficiency recycling method for Mo and Ni from spent catalyst via soda roasting and solvent extraction. Journal of Cleaner Production, 2022, 367: 132976.
DOI URL |
| [20] | 孙晓雪, 王德举, 王宁, 等. 碱性水热法浸出处理废弃钴钼加氢催化剂. 化学反应工程与工艺, 2023, 39(2): 126. |
| [21] |
FENG C L, ZHANG C, YUAN S H, et al. Sustainable recovery of surface-deposited oils and valuable metals from uncrushed spent hydroprocessing catalysts. Journal of Cleaner Production, 2022, 338: 130564.
DOI URL |
| [22] |
ZHOU C J, SU J, JIANG X H, et al. Numerical simulation and experimental verification for the sorting behaviors of mixed biomass particles in a novel Z-shaped fluidized bed. Chemical Engineering Journal, 2022, 441: 136109.
DOI URL |
| [23] |
LU S, LAN B, XU J, et al. Optimization of multiple-chamber fluidized beds using coarse-grained CFD-DEM simulations: regulation of solids back-mixing. Powder Technology, 2023, 428: 118886.
DOI URL |
| [24] |
WANG T, WANG P, YIN Z Y, et al. Hydro-mechanical analysis of particle migration in fractures with CFD-DEM. Engineering Geology, 2024, 335: 107557.
DOI URL |
| [25] |
ELASWAD R, EL-SHEIMY N, MOHAMAD A. Trajectory dynamics of particles in accelerated toroidal pipe: a computational study using CFD-DPM simulations. Journal of Computational Science, 2024, 78: 102285.
DOI URL |
| [26] |
BAI W, KELLER N K G, HEINDEL T J, et al. Numerical study of mixing and segregation in a biomass fluidized bed. Powder Technology, 2013, 237: 355.
DOI URL |
| [27] |
WANG S, SHEN Y S. CFD-DEM study of biomass gasification in a fluidized bed reactor: effects of key operating parameters. Renewable Energy, 2020, 159: 1146.
DOI URL |
| [28] |
KAZEMI S, ZARGHAMI R, MOSTOUFI N, et al. CFD-DEM mixing of rod-like and spherical particles in fluidized beds. Powder Technology, 2024, 442: 119847.
DOI URL |
| [29] |
HE L P, LIU Z X, ZHAO Y Z. Study on a semi-resolved CFD-DEM method for rod-like particles in a gas-solid fluidized bed. Particuology, 2024, 87: 20.
DOI URL |
| [30] |
ZHAO L J, TAN Z, ZHANG X G, et al. Study on fluidized roasting of spent hydrodesulphurisation catalysts in large-scale industrial boiling furnace by CFD simulation. Energy, 2024, 302: 131818.
DOI URL |
| [31] |
LEE S J, AHN H S, LEE J H, et al. Granule efficiency evaluation process using two-way CFD-DEM coupling analysis. Chemical Engineering Journal, 2024, 498: 155123.
DOI URL |
| [32] |
XIE Z Z, SHEN Y S, TAKABATAKE K, et al. Coarse-grained DEM study of solids sedimentation in water. Powder Technology, 2020, 361: 21.
DOI URL |
| [33] |
YANG X L, WANG S B, YANG J T, et al. Study on heterogeneous gas-solid structure and interparticle collision behavior in a vibrated fluidized bed of Geldart D particles using CFD-DEM simulations. Powder Technology, 2023, 427: 118691.
DOI URL |
| [34] |
ZHU L T, HE J F, YANG B. Ultrasound-enhanced separation characteristics of gas-solid fluidized bed for fine-grained fluorite ore. Advanced Powder Technology, 2024, 35(1): 104293.
DOI URL |
| [35] |
PINHEIRO D R, DE F NEVES R, PAZ S P A. A sequential Box-Behnken design (BBD) and response surface methodology (RSM) to optimize SAPO-34 synthesis from Kaolin waste. Microporous and Mesoporous Materials, 2021, 323: 111250.
DOI URL |
| [36] |
ARABKHANI P, ASFARAM A, ATEIA M. Easy-to-prepare graphene oxide/sodium montmorillonite polymer nanocomposite with enhanced adsorption performance. Journal of Water Process Engineering, 2020, 38: 101651.
DOI URL |
| [37] |
BAGHERI R, GHAEDI M, ASFARAM A, et al. RSM-CCD design of malachite green adsorption onto activated carbon with multimodal pore size distribution prepared from Amygdalus scoparia: kinetic and isotherm studies. Polyhedron, 2019, 171: 464.
DOI URL |
| [38] |
CHEN A R, WANG S X, ZHANG L B, et al. Optimization of the microwave roasting extraction of palladium and rhodium from spent automobile catalysts using response surface analysis. International Journal of Mineral Processing, 2015, 143: 18.
DOI URL |
| [39] |
CHEN Z Y, NIU B, ZHANG L G, et al. Vacuum pyrolysis characteristics and parameter optimization of recycling organic materials from waste tantalum capacitors. Journal of Hazardous Materials, 2018, 342: 192.
DOI PMID |
| [40] |
YUAN Y Z, ZHANG Y M, LIU T, et al. Optimization of microwave roasting-acid leaching process for vanadium extraction from shale via response surface methodology. Journal of Cleaner Production, 2019, 234: 494.
DOI URL |
| [1] | 杨恩东, 李宝乐, 张珂, 谭鲁, 娄永兵. ZnCo2O4-ZnO@C@CoS核壳复合材料的制备及其在超级电容器中的应用[J]. 无机材料学报, 2024, 39(5): 485-493. |
| [2] | 穆宏赫, 王鹏飞, 施宇峰, 张中晗, 武安华, 苏良碧. 热交换坩埚下降法制备大尺寸氟化铈晶体的热场设计与优化[J]. 无机材料学报, 2023, 38(3): 288-295. |
| [3] | 史艳磊, 孙聂枫, 徐成彦, 王书杰, 林朋, 马春雷, 徐森锋, 王维, 陈春梅, 付莉杰, 邵会民, 李晓岚, 王阳, 秦敬凯. 半密封直拉法生长6英寸磷化铟单晶热场研究[J]. 无机材料学报, 2023, 38(3): 335-342. |
| [4] | 陈士昆, 王楚楚, 陈晔, 李莉, 潘路, 文桂林. 磁性Ag2S/Ag/CoFe1.95Sm0.05O4 Z型异质结的制备及光催化降解性能[J]. 无机材料学报, 2022, 37(12): 1329-1336. |
| [5] | 李佳艳, 蔡敏, 武晓玮, 谭毅. 多晶硅太阳能电池片的回收再利用研究[J]. 无机材料学报, 2018, 33(9): 987-992. |
| [6] | 陈文波, 陈伦江, 刘川东, 程昌明, 童洪辉, 朱海龙. 射频热等离子体制备球形氧化铝粉末的数值模拟及实验研究[J]. 无机材料学报, 2018, 33(5): 550-556. |
| [7] | 邹俭鹏, 杨洪志, 肖 平, 潘一峰. 微纳分级结构碳酸钙中空微球的可控制备[J]. 无机材料学报, 2016, 31(7): 711-718. |
| [8] | 韩丹丹, 景晓燕, 徐鹏程, 谭 奥, 程振玉. NiO微球的微波辅助合成及电荷传导能力优化[J]. 无机材料学报, 2016, 31(6): 667-672. |
| [9] | 王晓媛, 闫亚宾, 嶋田隆広, 北村隆行. 纳米铁电材料铁电性及其力电耦合特性的原子尺度模拟研究[J]. 无机材料学报, 2015, 30(6): 561-570. |
| [10] | 刘文魁, 周伟昌, 张清林, 潘安练, 庄秀娟, 万 强. 分级介孔结构组成的ZnO微球及光催化性能[J]. 无机材料学报, 2013, 28(8): 875-879. |
| [11] | 刘光霞, 王圣来, 丁建旭, 孙 云, 刘文洁, 朱胜军. 转速对KDP晶体成帽影响的数值模拟研究[J]. 无机材料学报, 2013, 28(06): 665-670. |
| [12] | 陈 丰, 陈志刚, 钱君超, 刘成宝, 王 炜. 以枫叶为模板合成分级多孔氧化铈材料及其催化性能[J]. 无机材料学报, 2012, 27(1): 69-73. |
| [13] | 周 颖, 王志超, 王春雷, 王六平, 许钦一, 邱介山. 大孔 - 介孔分级孔结构炭材料制备及性能 研究[J]. 无机材料学报, 2011, 26(2): 145-148. |
| [14] | 孙天拓, 林 健, 魏恒勇, 冯昭彬. 银纳米晶掺杂玻璃基片对Er3+/Yb3+共掺碲酸盐薄膜的荧光增强及其数值模拟[J]. 无机材料学报, 2011, 26(11): 1215-1220. |
| [15] | 王维清,冯启明,董发勤,李虎杰,赵晓东. Fe3O4/斜发沸石磁性复合材料的制备及其性能[J]. 无机材料学报, 2010, 25(4): 401-405. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||