二维材料因其区别于体相的超薄原子结构、大的比表面积和量子限域效应等受到了人们的广泛关注[1-4] 。如何高分辨表征二维材料的晶相、晶格取向、堆垛方式及缺陷等对于其改进合成工艺、提高材料物性研究和性能应用是至关重要的。目前, 二维材料高分辨精细结构通常利用电子显微技术和扫描探针显微镜进行表征分析, 如扫描电子显微镜SEM、透射电子显微镜TEM、扫描隧道电子显微镜STM等, 由于其超高的放大倍数以及电子成像原理, 引领研究人员探究材料高分辨精细结构。而光学显微技术对样品形态、测试环境无严格要求, 且具有操作简单、测试成本低、无损检测等优点, 成为电子显微镜进行高分辨微结构表征的有益补充。二次谐波(Second Harmonic Generation, SHG)是近年发展起来的一种光学显微表征技术, 基于光与具有较大极化率的非中心对称物质的非线性相互作用, 二次谐波显微成像技术由于其无光损伤、无光毒性、无光漂白等特点, 近来广泛应用于生物组织结构的无创检测[5,6,7], 如生物组织内原纤维的取向检测[8]、肿瘤基质胶原的检测[9]等; 另外, 各种微纳结构中的二次谐波产生特性具有信号稳定、波长可调谐、相干性好、超快响应性和偏振敏感性等独特优点, 作为新型微纳相干光源, 在显微成像、精密探测和非线性微纳光学器件等领域有重要的应用前景[10,11,12,13,14,15]。其中, 二次谐波结合共聚焦光学成像技术获得空间光学衍射极限分辨率在二维材料晶格取向、晶界和堆垛等结构表征方面发挥了重要作用[16,17,18,19], 为科研工作者深入分析二维材料微观结构、物理性质等提供了重要参考[2,20-21]。由于二次谐波的产生并不依赖光子吸收过程, 光子与材料作用时保持能量守恒, 避免了测试过程对材料结构的破坏; 二次谐波测量不需要对材料进行特殊处理, 可以简化实验过程并避免外源性处理对材料结构的影响[22]。
本文将在二次谐波产生的原理和基本条件的基础上, 以飞秒脉冲激光接入共聚焦拉曼显微测试系统为参考介绍二次谐波产生的实验装置和测试方法, 并着重讨论二次谐波在二维材料堆垛、晶界、异质结、应力和缺陷表征中的优势与前沿进展, 同时也探索二次谐波与拉曼光谱、光致发光的多维度关联分析在材料全面深度表征方面的重要性。
1 二次谐波产生的基本原理
图1
非线性介质的光学响应可以通过介质的电极化强度P与入射辐射的光场强度E来确定, 介质在外加光电场作用下的极化强度可以表示为:
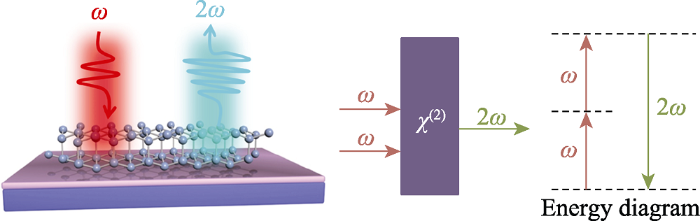
其中, ε0表示真空介电常数, χ(i)代表i阶非线性光学系数, 表示非线性材料的极化性质和非对称性, E代表光电场的强度。χ(1)为一阶线性极化率, 用于表述传统的线性光学性质, 如折射、散射和吸收; χ(2)代表二阶极化率, 反映了二阶非线性光学效应, 如差频、和频和倍频等。其中目前应用最广泛的是倍频, 即二次谐波, 是指在强电场作用下, 具有相同频率的两个光子与非线性介质相互作用后, 产生具有初始光子两倍能量的新光子, 其频率加倍, 波长减半。二次谐波过程并不发生能量跃迁, 两个频率为ω的入射光子的能量等于一个频率为2ω发射光子的能量。根据能量守恒, 介质分子的量子力学状态并不会发生改变, 即被激发样品不会吸收能量。二次谐波不仅与光电场强度E有关, 还与介质的二阶极化率χ(2)有关。二次谐波的强度可以简化表示为:
其中, $\vec{P}$为电介质中二次谐波的电极化强度矢量, $\vec{E}$是基频入射光强度矢量[25]。
在进行空间反演对称操作时, 二阶电极化强度矢量和基频入射光强度矢量都改变符号, 而计算出的电极化强度保持不变, 则$x^{(2)}=0$。即对于具有中心反演对称性的介质, 其二阶极化率为零, 若材料具有二次谐波现象, 则反映了其中心反演对称性是被破坏的[23]。因此, 可以通过二次谐波现象表征材料的结构对称性信息。
对于打破中心反演对称性的介质, 其二次谐波的强度$P_{2 \omega}$和频率转化效率η可以分别通过下式表示:
其中, $P_{2 \omega}$和$ P_{\omega}$分别为倍频和基本激光功率; $\varepsilon_{0}$和c分别为真空中的介电常数和光速; A为入射激光光斑的面积; λ为入射光波长; d为样品的厚度; $n_{2 \omega} $和$n_{\omega} $分别为样品在倍频和基本激光频率下的折射率。当$n_{2 \omega}=n_{\omega}$时, 满足相位匹配条件, 二次谐波的转化效率与入射光场和非线性介质的作用长度的平方成正比[23]。当入射光电场取向为$\hat{e}_{\omega}$时, 产生的二次谐波在$\hat{e}_{2 \omega}$出射方向的强度可以用下式(5)描述:
其中,$\mathrm{eff}$定义为有效二阶非线性系数, $d_{\mathrm{eff}}=1 / 2 \chi^{(2)}$。
2 飞秒脉冲激光接入共聚焦拉曼显微测试系统
本文基于以飞秒脉冲激光接入共聚焦拉曼显微测试系统为基础, 介绍二次谐波的产生装置和测试方法。采用美国相干公司Chameleon Ultra II fs激光器产生的脉冲激光, 脉冲宽度140 fs, 重复频率80 MHz, 输出波长范围680~1600 nm。将飞秒激光通过自由光路引入到alpha 300R共聚焦拉曼显微镜, 具体地, 激光通过光参量振荡器调制, 经过一个可调衰减片调节激光功率和一系列光学组件后, 进入WITec alpha300RS+共聚焦拉曼显微镜, 最后被显微镜头(100倍)聚焦为直径1.8 μm的光斑; 二次谐波产生的信号通过同一显微镜头收集, 并通过一个低通高滤的滤波片进入拉曼光谱仪。对于角度依赖的二次谐波, 为确保入射激光为线偏光, 在入射光路中增设偏振片和半波片。同时, 为检测二次谐波沿特定方向偏振的强度, 在收集光路中也增设偏振片, 使得偏振方向与入射偏振方向一致。
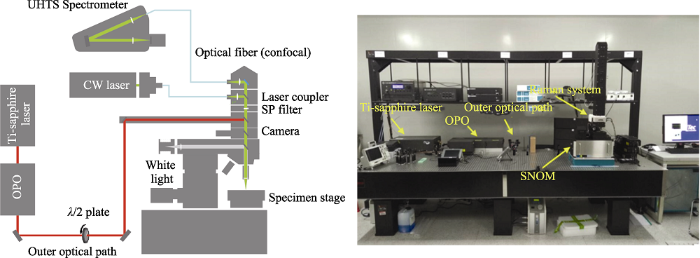
该系统扩展了共聚焦拉曼光学显微镜自身的功能与应用, 将二次谐波非线性成像与光学图像、拉曼图像以及光致发光成像进行联用, 对于更全面了解与掌握样品的结构对称性、晶格取向、原子层堆垛、晶界等性质起到了推动作用。二次谐波产生装置示意图和实物图如图2所示。
图2
图2
二次谐波产生装置示意图和实物图
Fig. 2
Schematic diagram and picture of the experimental setup of SHG
3 二次谐波表征二维层状材料的堆垛
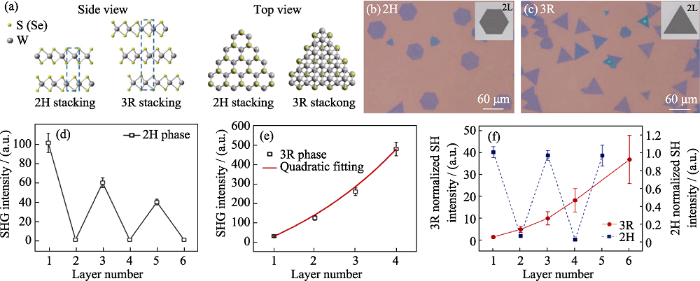
二维层状材料的结构对称性可以分成两类: 非中心对称性和中心对称性[26,27,28,29,30,31]。二次谐波对于少层二维材料的晶体对称性异常敏感[26-27,29,32-38]。对于非中心对称性材料, 其本征具备二次谐波信号, 如3R相的MX2(其中M为Mo, W等, X为S, Se等)[39], 1T‴相MoS2、InSe、GeTe等。对于中心对称结构, 如2H相的MX2, 随着原子层数的变化, 其所属的空间群发生变化, 二次谐波信号将产生波动性变化, 对于奇数层数的2H相, 由于奇数层的结构转变, 二次谐波信号的增强, 对于偶数层的2H相则二次谐波信号泯灭。因此, 通过二次谐波表征材料的不同堆垛方式、堆垛层数、层间堆垛角度, 信号会表现出不同的相对强度。Zeng等[40]通过二次谐波表征不同相的WS2, 得到截然不同的层数与二次谐波信号强度的依赖关系。对于二次谐波信号强度呈现震荡趋势改变的二维WS2(图3(d)), 其单层为非中心对称结构, 二次谐波信号较强, 对于两层WS2, 二次谐波信号泯灭, 这种信号强度的反差可以归因为第二层S原子和W原子都堆垛于第一层相应原子的正上方, 两层的WS2恢复了反演对称结构。在中心对称偶数2N层中, 相邻层产生的SH场相互抵消, 导致没有二次谐波信号。对于奇数层, 只在(2N±1)层中产生残留的二次谐波信号。根据这种二次谐波信号呈现出振荡减小的趋势能够定性表征少层二维材料的相对厚度。随着样品层数增加依次增强的二次谐波信号(图3(e)), 表明各层均为非中心对称结构, 层间堆垛方向由AB堆垛改变为非中心对称性堆垛, 在平面内发生位移导致面内非线性偶极子和非零的二阶非线性极化率, 不同层的非线性偶极子相互叠加, 形成逐渐增强的二次谐波信号, 对于这种少层的二维材料, 通过拟合发现ISHG正比于层数N的平方, 这和3R相少层二维材料WSe2的二次谐波信号强度与层数拟合结果一致[40]。Zhao等[41]通过二次谐波表征了不同相MoS2也得到了层数与二次谐波信号强度的依赖关系: 对于2H相, 随着层数增加二次谐波信号产生波动性变化, 奇数层数表现出二次谐波信号增强, 偶数层的2H相则表现出二次谐波信号泯灭; 对于3R相MoS2, 随着层数增加二次谐波信号强度依次增强[41]。这与3R和2H相WS2二次谐波信号强度随层数变化的结论基本一致。因此, 根据二次谐波信号的相对强度, 在明确了结构对称性的基础上, 能够进一步对层间堆垛方式进行表征, 根据二次谐波信号强度的变化趋势能够定性表征少层二维材料的相对厚度。
图3
图3
二次谐波表征不同堆垛层数的二维层状晶体
Fig. 3
Characterization of 2D layered crystals with different stacking layers by SHG
(a) Side view and top view of atomic structure illustration of typical layered WS2 with 2H and 3R stacking; (b-c) Optical images of 2H and 3R phase WS2; (d-e) SHG intensity of 2H and 3R phase WS2 as a function of layer numbers[40]; (f) SHG intensity of 2H and 3R phase MoS2 as a function of layer numbers[41]
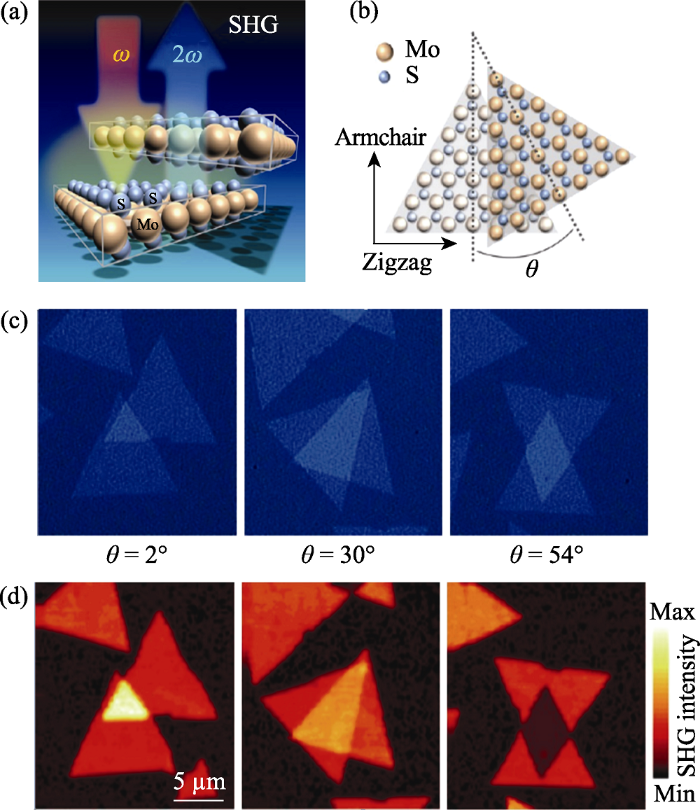
除了表征二维材料堆垛层数, 由于对晶体取向的敏感特性, 二次谐波能够进一步表征原子层间堆垛角度。Hsu等[42]人工堆垛得到层间扭曲的MoS2/MoS2、WSe2/MoS2、WSe2/WS2双层薄膜, 通过二次谐波的强度结合偏振来表征层间堆垛角度(图4)。当双层堆垛角度改变时, 二次谐波强度也发生明显改变。其中, 当二维材料的扶手椅方向与入射激光偏振方向$\vec{E}$(ω)间的夹角分别为φ1、φ2时, 则第一层和第二层产生的二次谐波$\vec{E}_{1}$ (2ω)、$\vec{E}_{2}$ (2ω)与入射激光偏振$\vec{E}$ (ω)间的角度分别为3φ1、3φ2, 双层堆垛区域的二次谐波电场$\vec{E}_{S}$ (2ω)则是$\vec{E}_{1}$ (2ω)、$\vec{E}_{2}$ (2ω)的矢量和: $\vec{E}_{S}$ (2ω)= $\vec{E}_{1}$ (2ω)+ $\vec{E}_{2}$ (2ω)。双层堆垛区域总的二次谐波强度正比于|$\vec{E}_{S}$ (2ω)|2, 用二次谐波强度表示为: $I_{\mathrm{s}}(\theta)=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos 3 \theta$, 其中$I_{S}、I_{1}、I_{2}$分别为堆垛区域、第一单层和第二单层的二次谐波强度, θ为第一层和第二层间的堆垛角度, 等于φ1、φ2的差值。当两层的堆垛角度在0°~60°之间变化时, $ I_{S}$呈周期性改变, 当θ=0°时, 堆垛区域的二次谐波强度是两个单层相长干涉, 相当于3R相堆垛, $I_{S}$最大。当θ=60°时, 堆垛区域的二次谐波强度是两个单层相消干涉, 相当于 2H 相堆垛, 导致$I_{S}$最小[42]。因此, 根据这种双层堆垛二维材料二次谐波极化方向的矢量叠加原理, 通过堆垛区域的二次谐波强度的相对强弱, 可以进一步表征二维材料堆垛层之间的角度。
图4
图4
二次谐波表征层间堆垛角度
Fig. 4
Characterization of stacking angle between layers by SHG
(a) Schematic of SHG process in second harmonic generation of bilayer thin film; (b) Atomic structure of artificially stacked bilayer; (c-d) Optical images for stacked bilayers with different stacking angles and their corresponding SH intensities[42]
4 二次谐波精准定位二维材料晶界
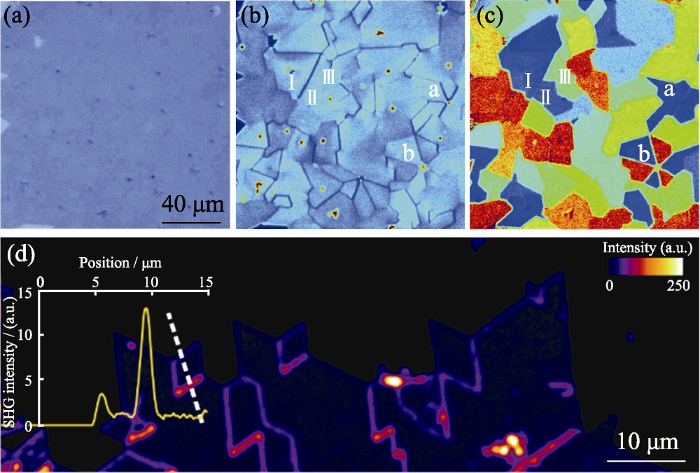
由于晶体表面对称性破坏能够形成二维电子态。对于单层的二维晶体, 晶体边缘的电子结构变化会产生较强的非线性光学敏感度, 从而通过二次谐波能够对二维材料的原子边缘和边界直接成像。另外, 通过施加偏振泵浦光, 也可以在大范围内快速、全光学地确定二维材料的晶体取向。Yin等[43]研究了CVD生长的大面积六方二硫化钼(MoS2)薄膜一维边缘和边界上的二阶非线性光学。由于反转对称性被破坏, MoS2薄膜呈现出强烈的二次谐波现象。同时, 相邻区域的单层之间存在将不同晶粒连接在一起的几个原子宽的线缺陷, 即晶界, 导致非线性波的相消干涉与湮灭。因此, 二次谐波成像可以区分晶粒和晶界。相比于均匀的光学图像(图5(a)), 二次谐波图像(图5(b))揭示了均匀单层的多晶性质。每个晶粒内均匀的二次谐波强度表明其是单晶。然而, 在晶界处, 由于具有不同取向的相邻晶粒产生的二次谐波相消干涉和湮灭, 二次谐波基本上被抑制。虽然晶界宽度只有几个原子位, 但晶界清晰可见。通过测量边界处的二次谐波强度, 分析二次谐波的偏振成分, 还可以确定两个相邻晶体之间的夹角, 进而得到多晶单层MoS2的晶体取向图(图5(c))。这种方法能够捕捉到完整的晶粒结构图, 根据晶体方向进行颜色编码[43]。针对可视化显示对比度较弱, 或需要使用化学溶剂来增强图像对比度的问题, Carvalho等[44]进一步引入暗场二次谐波来增强显示单层MoSe2的晶界和边缘, 通过暗场二次谐波能够有效分离发射光成分, 并利用不同取向晶畴的干涉效应, 通过二次谐波发射将晶界和边缘定位为非常明亮的一维图案, 使晶界和边缘处更加清晰和直观[44]。
图5
图5
二次谐波表征二维材料晶界及晶体取向
Fig. 5
Characterization of the grain boundary and crystal orientation of two-dimensional materials by SHG
(a-b) Optical image and SHG image of a polycrystalline monolayer of MoS2 of the same area; (c) Polarized-SHG image showing the crystal orientations[43]; (d) Dark-field SHG imaging of a monolayer MoSe2[44]
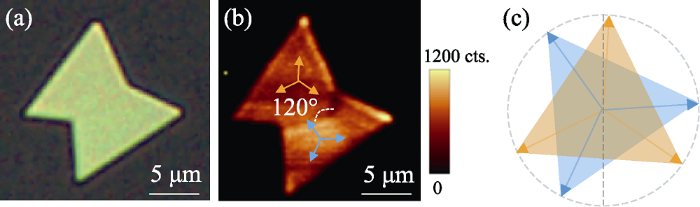
二次谐波图像在可视化表征晶界的同时, 还能有效地对晶粒的形成机理进行表征[45]。Hu等[24]通过CVD方法生长出二维Ge晶体, 利用WITec alpha300RS+显微共聚焦多场联用系统实现对样品的光学图像和二次谐波成像同区域表征。从光学图像(图6(a))知两个三角形Ge薄片连为一体, 不存在明显边界, 无法区分单晶或者两个晶粒; 二次谐波成像则能够明显分辨出晶界和晶畴(如图6(b)): 当来自相邻晶粒的信号相消干涉时, 在二次谐波图像中清晰可见较暗的分界线, 如图6(b)所示。而且偏振二次谐波测试可以得到两个晶畴的晶体取向之间的夹角(如图6(c))。在确定了两个Ge晶粒存在晶界和晶粒取向后, 由于晶体生长过程中相邻边缘的边界方向取决于相邻边缘的相对生长速率[45], 根据两个晶粒接触并继续生长时形成的对称倾斜边界, 揭示了两个晶粒相似的边以相同的间距合并, 随后边界将两条边平分, 从而形成对称的倾斜边界的生长机制。
图6
图6
二次谐波表征晶界及晶粒的形成机理
Fig. 6
Characterization of the grain boundary by SHG and analysis of grain formation mechanism
(a) Optical image and SHG mapping of the flake with boundary; Inset: illustration of the two edges growth at the boundary; (c) Illustration of the armchair directions of the two grains[24]
5 二次谐波检测应力和缺陷
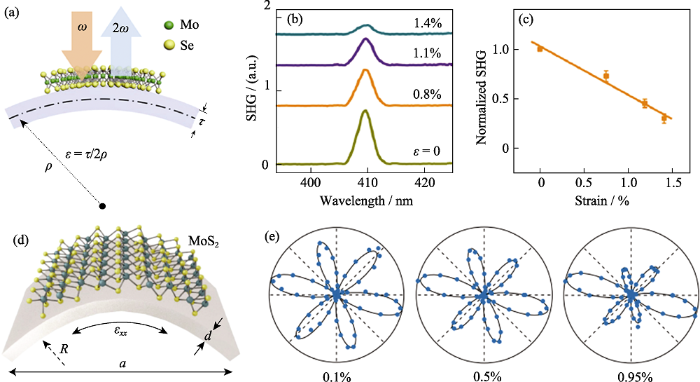
对二维层状材料施加外力产生的应变能够有效、可逆地调控二维材料的物理和化学性质, 如带隙、相图和反应活性。但是对局部点应变矢量进行完整表征仍然面临挑战。对于非中心对称的二维材料, 由于二次谐波光场强度与非线性光学系数成正比, 二次谐波强度对2D的结构变化异常敏感。当非中心对称的二维材料产生应变时, 其晶格结构随之发生改变, 进而引起非线性光学系数的变化。因此, 理论上, 采用二次谐波能够原位、灵敏且无损地测量非中心对称二维材料局部应变。Liang等[46]采用二次谐波对单层MoSe2进行单点应变强度、应变方向进行了表征(图7(b))。对于单层MoSe2, 通过改变基底的形变量获得不同的MoSe2应变, 并采集不同应变下的二次谐波强度, 得到$\frac{\Delta I_{\varepsilon}}{I_{0}}=\frac{I_{\varepsilon}-I_{0}}{I_{0}}$, 其中$I_{\varepsilon}$和$I_{0}$分别是应变和无应变下的二次谐波强度, 也即二次谐波强度随应变呈线性改变, 且斜率比PL峰值强度的相对变化大一个数量级。因此, 通过监测二次谐波强度变化可以更加灵敏地对应变进行调控。另外, Mennel等[47]用两点弯曲法对MoS2施加不同的单轴拉伸应变, 通过光弹性张量建立起应变和非线性磁化率之间的关系[48], 测量偏振分辨二次谐波信号强度, 通过三个偏振倍频测量点确定局部应变张量, 实现高效快速的应变场成像(图7(d, e)), 补充和扩展了已有的光学应变测量方法, 使用这种技术, 可以在亚皮秒时间尺度上表征瞬态晶体变形[47]。因此, 基于二次谐波对于应变的灵敏反应, 二次谐波强度可以直接、灵敏地监测应变幅度。
图7
图7
二次谐波表征二维材料应变
Fig. 7
Characterization of the strain of 2D materials by SHG
(a) Schematic of strain apparatus and SHG process in monolayer MoSe2 under uniaxial tensile strain; (b) SHG spectra under different strain; (c) Evolution of normalized SHG intensity with strain[46]; (d, e) Schematic illustration of two-point bending method and SHG patterns for applied tensile strains of 0.1%, 0.5%, and 0.95%[47]
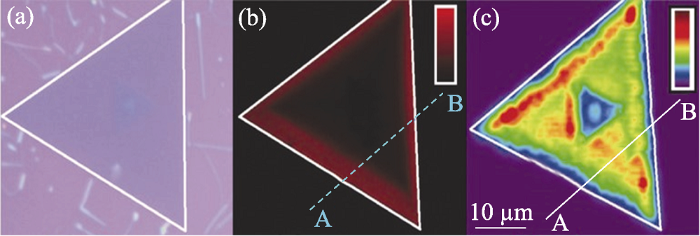
此外, 随着材料缺陷的引入, 材料的性能也得以控制或调整[49,50]。通常采用STEM、PL等表征材料缺陷。近来, 二次谐波也被用于单层材料缺陷的可视化表征。对于缺乏反转对称性的单层过渡金属二硫化物, 二次谐波信号的变化可用于跟踪材料中的缺陷密度, 对于衍射受限的激光束, 空间分辨率通常能够达到亚微米量级。Rosa等[51]通过化学气相沉积制备了单层WS2, 并用二次谐波可视化表征其缺陷, 二次谐波信号随材料中缺陷的密度而变化, 对于单层WS2, 二阶非线性极化率可能会由于缺陷相关的中能隙态的存在而在红外波段得到改善, 进而用来区分低缺陷区和高缺陷区(图8)。在缺陷区, 硫原子被空位取代, 二次谐波信号得到增强, 高达2个数量级。密度函数理论计算也表明, 这种与空位相关的缺陷在材料的能带结构中产生了中能隙态, 当WS2的光学带隙为1.9 eV时, 中能隙态距离价带顶部约1.5 eV, 使得基波(1560 nm)的倍频(780 nm)成为准共振过程, 因此, 在780 nm处的二次谐波图像能够清晰直观地区分出高低缺陷区, 在缺陷密度高的区域, 二次谐波得到显著增强, 进而实现高缺陷密度区域的可视化识别[51]。因此, 通过二次谐波信号的变化来跟踪材料中的缺陷, 能够快速、无损地表征材料的缺陷区域。
图8
图8
二次谐波表征二维材料的缺陷
Fig. 8
Characterization of the defects of 2D materials by SHG
(a-c) Optical image, fluorescence image and second harmonic mapping image of monolayer WS2[51]
6 二次谐波与拉曼光谱、光致发光光谱的多维度关联分析
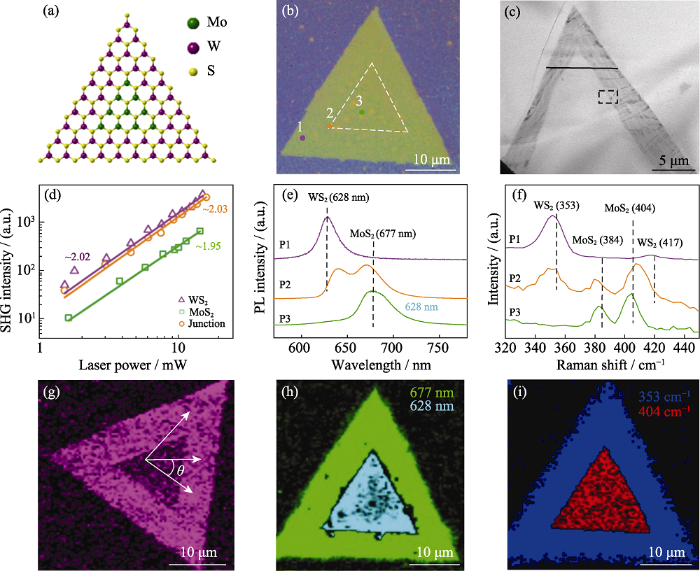
集成了非线性光学表征功能的共聚焦拉曼显微测试系统可以实现同区域的拉曼、光致发光(Photoluminescence, PL)和二次谐波非线性光学成像的联用, 这能够帮助研究者更全面地了解二维材料样品的晶体结构。Wu等[52]利用WITec alpha300RS+显微共聚焦拉曼成像系统对MoS2/WS2异质结分别进行二次谐波、拉曼和PL表征。首先, 通过光学图像(图 9(b))发现合成的二维材料样品为均匀的三角形结构, 进一步采用TEM观察异质结构。同时, 采集二次谐波在400 nm处图像, 均存在较强的二次谐波响应, 且在核壳处存在清晰边界; 但是中间三角形区域的响应强度低于边缘区域, 进一步证实了异质结的存在。通过进一步对光学图像中不同位置处进行PL和拉曼表征, PL光谱(图9(e))呈现两个特征发射峰, 外层约628 nm和内层约677 nm处出现的峰值分别归因于WS2和MoS2的近带边发射; 同时, 对应的PL映射(图9(h))显示, 核(MoS2)和壳(WS2)区域都显示出均匀和明亮的对比度变化, 进一步表明其元素分布均匀, 同时, 在异质结界面处, 发光位置呈现出两个特征峰, 且相较于MoS2和WS2, 峰位均出现了一定的偏移, 这可归因于MoS2和WS2晶格常数不同导致晶格失配所引起的应变。同区域拉曼表征进一步证实由该区域产生的两个特征峰属于单层MoS2, 在404 cm-1处为A1g振动模式, 在384 cm-1处为E2g振动模式; 同时, 在壳区域417和353 cm-1处呈现的两个拉曼峰分别对应于WS2的A1g和E2g振动模式。从异质结界面处收集的光谱同时包含MoS2和WS2共振模式, 进一步证实了在该区域两个不同相共存的性质。因此, 通过将二次谐波表征引入共聚焦拉曼显微成像系统, 采用二次谐波、PL和拉曼进行同区域表征, 得到的材料结构信息能够互相补充和相互印证, 为更加全面地探知二维材料的结构信息提供便捷的测试手段。
图9
图9
二次谐波与光致发光、拉曼光谱联合表征二维材料(MoS2/WS2异质结)
Fig. 9
Characterization of 2D materials (MoS2/WS2 heterojunction) by SHG combined with photoluminescence and Raman spectroscopy
(a) Atomic structure diagram; (b-c) Optical image and TEM image; (d, g) SHG intensity and mapping; (e, h) photoluminescence spectra at different positions; (f, i) Corresponding Raman spectra[52]
7 总结和展望
总之, 二次谐波在二维材料的研究中得到了广泛的应用, 具有对晶体对称性敏感、非接触、无损伤、无需制备和易于操作等优点。本文着眼于二次谐波在二维材料结构表征中的应用, 介绍了二次谐波产生机理、测试装置和方法, 重点阐述了二次谐波在二维材料层间堆垛、相结构、晶界、晶体取向、晶体缺陷等结构表征方面的应用, 同时, 二次谐波与拉曼光谱、光致发光的多维度关联分析在材料全面深度表征方面发挥着重要作用。最后, 二次谐波作为一种重要的二维材料结构表征手段, 未来将会在二维材料研究中发挥越来越重要的作用。例如, 对于新兴的二维磁性材料[53,54,55], 采用二次谐波可以进一步研究磁有序结构、磁畴和超快磁动力学等[55]。随着二维材料的相变引起了研究者广泛关注[56,57], 未来也可以采用二次谐波对相变材料的结构转变进行表征。
参考文献
Electronics and optoelectronics of two-dimensional transition metal dichalcogenides
Second harmonic generation spectroscopy on two-dimensional materials [Invited]
ReX2 (X=S,Se): a new opportunity for development of two-dimensional anisotropic materials
Research progress of direct growth of two-dimensional hexagonal boron nitride on dielectric substrates
Black phosphorus nanosheets as a neuroprotective nanomedicine for neurodegenerative disorder therapy
Quantitative second harmonic generation microscopy for the structural characterization of capsular collagen in thyroid neoplasms
Second-harmonic generation from biological tissues: effect of excitation wavelength
Orientation fields of nonlinear biological fibrils by second harmonic generation microscopy
Prognostic value of tumor stromal collagen features in patients with hepatocellular carcinoma revealed by second-harmonic generation microscopy
Crystal growth, structural, optical and piezoelectric investigations on novel B4AAT (bis-4-acetylanilinium tartrate): a phase matchable second and third-order NLO single crystal for optoelectronic and nonlinear optical device applications
Enhancing the SHG effect of zinc chloride-doped DAST single crystals: new potential materials for nonlinear optical device applications
Optical second harmonic generation from silicon (100) crystals with process tailored surface and embedded silver nanostructures for silicon nonlinear nanophotonics
Synthesis, growth and optical, mechanical, electrical and surface properties of an inorganic new nonlinear optical crystal: sodium cadmium tetra chloride (SCTC)
Structuring nonlinear wavefront emitted from monolayer transition-metal dichalcogenides
Second harmonic generating (SHG) nanoprobes for in vivo imaging
Improvement of second-harmonic generation induced by structural distortions in Nb doped YCa9(VO4)7 crystals
Large enhancement of second-harmonic generation in MoS2 by one dimensional photonic crystals
Precise characterization of self-catalyzed III-V nanowire heterostructures via optical second harmonic generation
Synthesis of InSe nanoflakes with near-infrared photoresponse grown by chemical vapor deposition
Second harmonic generation of two-dimensional layered materials: characterization, signal modulation and enhancement
Space-confined chemical vapor deposition synthesis of ultrathin HfS2 flakes for optoelectronic application
Nonlinear optics of two-dimensional transition metal dichalcogenides
Halide-induced self-limited growth of ultrathin nonlayered Ge flakes for high-performance phototransistors
Sub-millimeter-scale monolayer p-type H-phase VS2
Phase-engineered growth of ultrathin inse flakes by chemical vapor deposition for high- efficiency second harmonic generation
Inversion symmetry broken 2D 3R-MoTe2
Honeycomb RhI3 flakes with high environmental stability for optoelectronics
Sr6Cd2Sb6O7S10: strong SHG response activated by highly polarizable Sb/O/S groups
Emerging in-plane anisotropic two-dimensional materials
Phase-engineered synthesis of ultrathin hexagonal and monoclinic GaTe flakes and phase transition study
Robust piezo-phototronic effect in multilayer gamma-InSe for high-performance self-powered flexible photodetectors
Structural determination and nonlinear optical properties of new 1T‴-type MoS2 compound
Self-confined growth of ultrathin 2D nonlayered wide-bandgap semiconductor CuBr flakes
2D inorganic bimolecular crystals with strong in-plane anisotropy for second-order nonlinear optics
Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation
Activation of new raman modes by inversion symmetry breaking in type II weyl semimetal candidate T'-MoTe2
Second harmonic generation in atomically thin MoTe2
Controlled vapor growth and nonlinear optical applications of large-area 3R phase WS2 and WSe2 atomic layers
Atomically phase-matched second-harmonic generation in a 2D crystal
Second harmonic generation from artificially stacked transition metal dichalcogenide twisted bilayers
Edge nonlinear optics on a MoS2 atomic monolayer
Nonlinear dark-field imaging of one-dimensional defects in monolayer dichalcogenides
Kinetic nature of grain boundary formation in as-grown MoS2 monolayers
Monitoring local strain vector in atomic-layered MoSe2 by second-harmonic generation
Optical imaging of strain in two-dimensional crystals
Second-harmonic generation from realistic film-substrate interfaces: the effects of strain
Second harmonic generation in defective hexagonal boron nitride
Second harmonic generation in two-dimensional transition metal dichalcogenides with growth and post-synthesis defects
Second-harmonic spectroscopy for defects engineering monitoring in transition metal dichalcogenides
Self-powered photovoltaic photodetector established on lateral monolayer MoS2-WS2 heterostructures
A magnetic sensor using a 2D van der Waals ferromagnetic material
2D ferromagnetism in layered inorganic-organic hybrid perovskites
Probing ferroelectrics using optical second harmonic generation
Millimeter-scale single-crystalline semiconducting MoTe2 via solid-to-solid phase transformation
Topological phase transition in 2D 1T′-WSTe