随着现代工业的不断发展与进步, 为了满足日益增长的能源系统需求, 人们对性能更加优异的储能材料与机理更加新颖的电能存储系统有着巨大的需求[1]。对于如何提高供电系统功率密度, 并同时降低其尺寸和成本的研究引起了工业技术领域和储能领域的高度重视。与其他电能存储设备相比, 由介电复合材料所制得的介质电容器在快速充放电能力与高功率密度方面极具优势, 受到了越来越多的关注与研究。
介质电容器的能量密度与电池和双层超级电容器等电化学设备相比仍有较大差距[2],因此,具有高能量密度的聚合物基介电复合材料的研究一直受到广泛关注。线性电介质的能量密度可以表示为:
进而表示为:
为解决上述问题, 研究者们分别基于无机填料的尺寸、形状和排布三方面对介电复合材料的介电常数与击穿强度进行调控。例如王立等[5]使用两步熔盐法控制无机填料的平均尺寸, 通过填充一定尺寸的无机填料提升了介电复合材料的介电性能; 刘晓林等[6]合成了珊瑚状和树枝状的无机填料, 通过其垂直于外电场的分支增加击穿强度, 平行于外电场的分支增大介电常数; 王逸飞等[7]通过调控无机填料的分布, 设计了一种类似三明治的宏观结构, 使其夹层结构中相邻层之间形成了更强的界面势垒, 从而实现了更优的击穿强度。上述研究都为改善介电复合材料介电常数与击穿强度之间的矛盾提供了新的途径。但是对于介电复合材料发生击穿损伤时, 如何通过其内部电场与击穿损伤形貌的演变规律优化介电及耐击穿性能的研究较少。
本研究通过有限元数值模拟, 基于DBM模型, 调控无机填料的体积含量, 改变其分布结构, 以聚二甲硅氧烷(PDMS)聚合物为基体, 设计出多种介电复合材料。探究了无机填料的分布对整个介电复合材料体系电场的影响, 继而阐明发生介电击穿时树状损伤通道的击穿损伤形貌的演变规律与特性。该研究结果通过提升介电复合材料的耐击穿性能来进一步提升能量密度, 为开发高储能密度的有机-无机介电复合材料提供理论指导。
1 实验方法
1.1 有限元数值模拟
有限元数值模拟法是由Richard Courant[8]于1943年首次提出, 其基本原理是: 将物理模型划分为由各个基本单元组成的集合, 在每个基本单元内采用插值多项式代替微分方程的解, 接着利用剖分插值, 将微分方程离散为一组多元的线性方程组, 最后以对单元节点插值的方式来得到计算区域内微分方程的近似解。
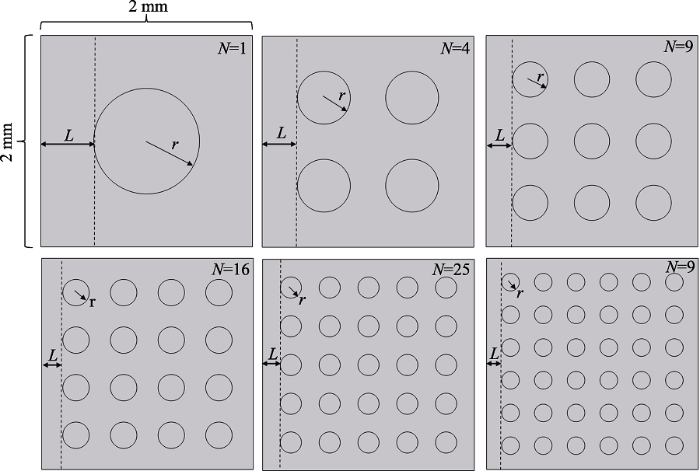
图1
根据几何原理计算得到:
其中, L为最边缘的球形填料同介电复合材料边缘的距离, r为球形填料的半径, N为球形填料的数量。
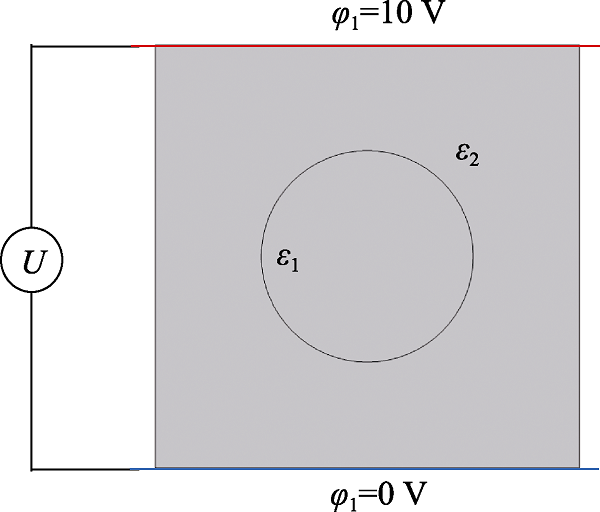
图2是类似于平行板电容器的几何模型, 以球形填料数量N=1时为例, 在进行有限元计算时, 该介电复合材料填料与基体的介电常数分别为
其中,
图2
图2
尺寸为2 mm×2 mm的正方形介电复合材料模型
Fig. 2
Model of square dielectric composite with size of 2 mm×2 mm
1.2 DBM模型
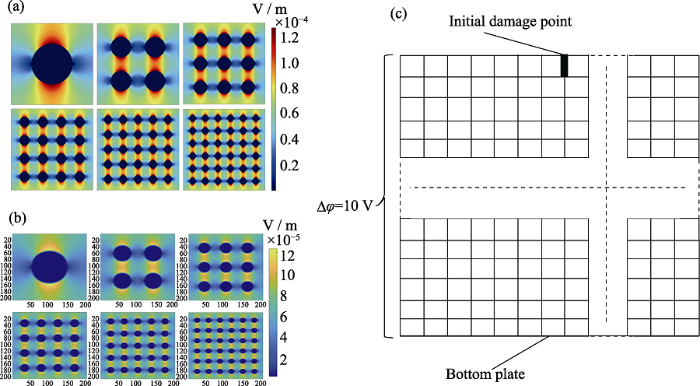
在DBM模型中, 电介质由矩形点阵表示, 其中的每个点都代表了一个电介质点[10]。如图3(a, b), 将使用有限元计算得到的电场强度以矩阵的形式导入数学软件MATLAB。再将其结果组成如图3(c)所示的正方形网格, 代表网状结构的聚合物基复合材料, 最后将其离散为由200×200个网格点组成的二维阵列。在二维阵列中设置并标记一个网格点为初始击穿的损伤点。损伤点随着计算的进行而不断拓展形成树状损伤通道。在计算过程中, 根据上一步损伤点周边网格点的局部场强定义其损伤的概率, 因此该模型的树状损伤通道决定于通道周边的局部场强, 但又不一定是在局部场强最大处不断损伤, 而是在损伤概率最大处, 从而使树状损伤通道的生长受到电场的随机控制。
图3
图3
DBM模型的计算方法
Fig. 3
Calculation method of DBM model
(a) Electric field distribution determined by finite element analysis; (b) Electric field distribution determined by MATLAB; (c) Two-dimensional array model consisting of 200×200 grid points
Colorful figures are available on website
树状损伤通道在上个损伤点周边网格点生长的概率P与该点处电场强度E的指数η次幂成正比
其中, 在树状损伤通道周边所有可能的生长位点为
2 结果与讨论
2.1 介电常数分析
本研究需要确定在有限元数值模拟中填料和基体的介电常数
图4
图4
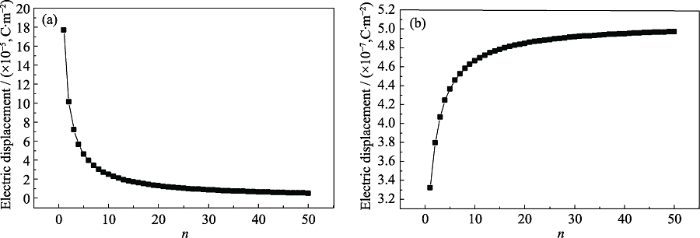
改变填料与基体介电常数之比时, 介电复合材料电位移的变化
Fig. 4
Electrical displacement evolution of dielectric composite material with varied ratio n between fillers and matrix dielectric constant
(a)When the dielectric composite filler is selected to be BaTiO3; (b) When the dielectric composite matrix is selected to be PDMS
当n从1到50变化时, 介电复合材料的电位移变化速度呈现先快后慢,最后趋于平稳的趋势, 尤其是当n>20时, 电位移的变化趋缓。文献[13]中向聚合物基体中加入一定含量(小于渗流阈值)的球形填料后, 介电复合材料整体的介电常数不会大幅度提高,实验现象与本研究的计算结果吻合。而在介电复合材料内部, 其电位移越大, 极化强度也越大, 越有利于提高其介电常数。这表明当n>20时, 介电复合材料内部的电位移变化不再明显, 其内部电极化逐渐饱和。此时的填料介电常数对介电复合材料整体介电常数的贡献减小, 这可能是由分散无机填料的去极化效应导致[14]。因此, 在本研究进行有限元计算并得到如图3(a)所示的电场云图时, 以PDMS为基体, BaTiO3为填料, 此时的无机填料与聚合物基体皆为常用在介电复合材料中的组分。这一方面更加符合实验中的实际情况, 另一方面, 无机填料与聚合物基体的介电常数之比n远大于20, 介电复合材料内部的电位移变化量最大, 无机填料介电常数对介电复合材料整体介电常数提升的贡献也达到最大, 为探究无机填料分布对介电复合材料体系电场及击穿损伤形貌的影响减小了聚合物基体的影响。
2.2 DBM模型中生长系数分析
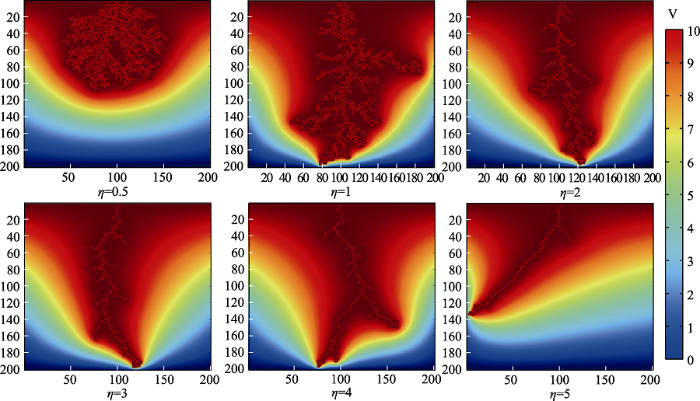
对纯聚合物基体进行DBM模型的计算, 观察生长系数
图5
图5
不同生长系数η时的树状损伤通道
Fig. 5
Dendritic damage channels with different growth coefficients(η)
Colorful figures are available on website
倘若该二维空间图形并不恰好是正方形, 而是具有特定形态的, 则此时式(8)中的N(r)不一定反比于r2, 便可以得到该二维空间图形的分形维数Df为:
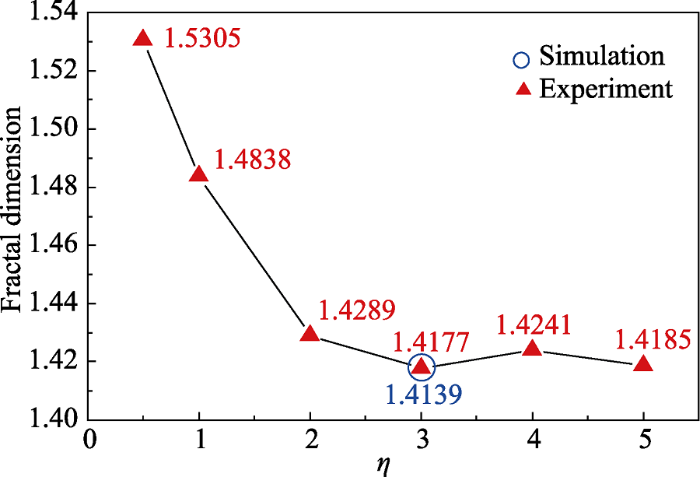
对比图5可以直观看出随着树状损伤通道的生长系数增大, 其分形维数减小。文献中实验得到的纯聚合物基体电树枝击穿损伤形貌[17]同本研究生长系数为3时计算DBM模型得到的电树枝形态最为相似。使用Matlab软件由式(9)编程计算各分形维数的结果也同样说明了这一点, 计算结果如图6所示, 生长系数η的变化影响了电树枝的生长, 随着生长系数增大, 分形维数整体上呈现减小趋势, 这与在纯聚合物基体中计算得到的文献结论一致[16]。此外, 计算文献中实际实验的击穿损伤形貌[17]得到的电树枝分形维数为1.4139, 接近生长系数为3时仿真计算结果的分形维数1.4177。为了更加符合实际实验中的情况, 本研究在后续添加无机填料的分析中, DBM模型中使用的生长系数
图6
图6
不同生长系数η时的电树枝分形维数
Fig. 6
Fractal dimension of electrical branche with growth coefficient η being altered
2.3 电场分布云图分析
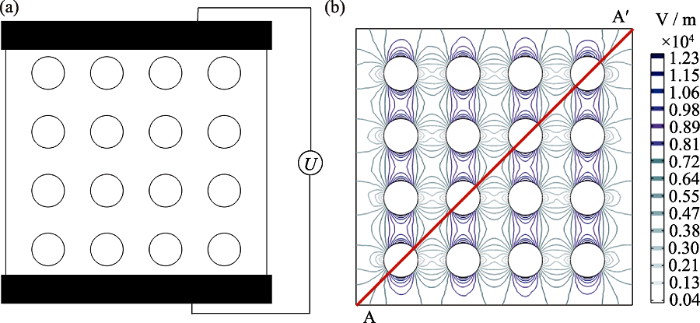
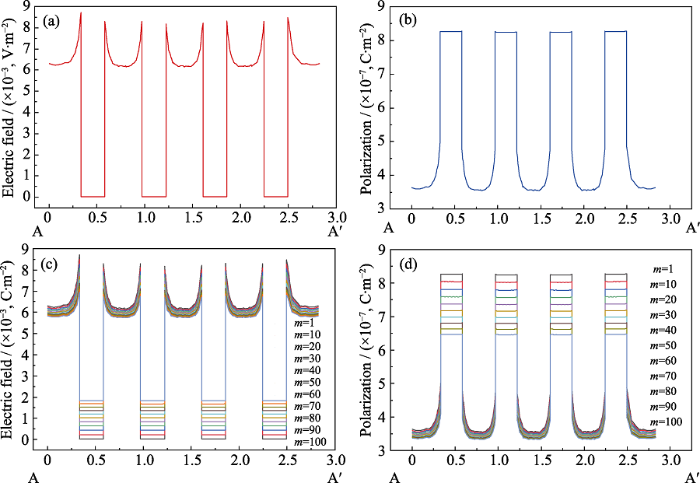
图7(a)为无机填料数量N=16时的模型示意图, 图7(b)显示了外加电场E和相应电势V的电场等值线图。由于填料颗粒与基体边界处的介电响应发生突变, 电场和极化的变化很大[18]。在图8(a)中, 沿截线AA'对电场进行的绘制, 可以发现, 无机填料和聚合物基体间的介电常数相差过大而导致介电差异, 无机填料内部的电场远低于外部, 且由于无机填料表面聚集较多的电荷, 材料内高电场集中分布在电场方向上的相邻填料之间, 从而形成了较高的局部电场[19]。在图8(b)中, 沿截线AA'对电极化场进行的绘制也同样说明了这一结论。之后, 为了探寻减少高电场集中分布的方法, 本研究将无机填料的介电常数缩小一定倍数m后, 再次沿截线AA'对复合电介质材料的电场与电极化场进行的绘制。由图8(c, d)可知, 聚合物基体和无机填料边界处的介电差异随着其介电常数的靠近而逐渐减小, 而由介电差异减小带来的高局部场强区域减小将增强介电复合材料的击穿强度[20]。因此,在进行介电复合材料的研究与制备中, 为减小其界面处高局部场强区域的大小, 提高材料的耐击穿能力, 应尽量选用介电常数较大的聚合物基体或介电常数较小的无机填料, 减小无机填料与聚合物基体边界处的介电差异。
图7
图7
电场分布分析
Fig. 7
Analysis of electric field distribution
(a) Dielectric composites composed of filler particles and matrix; (b) Internal electric field distribution in dielectric composites
Colorful figures are available on website
图8
图8
不同介电常数时的电场及电位移场分布
Fig. 8
Electric field and displacement field distribution with different dielectric constant
(a) Electric field distribution along AA' transversal; (b) Electric displacement field distribution along AA' transversal; (c) Electric field distribution along AA' transversal with dielectric constant of filler particles reduced by m times; (d) Electric displacement field distribution along AA' transversal with dielectric constant of filler particles reduced by m times
Colorful figures are available on website
2.4 击穿损伤形貌分析
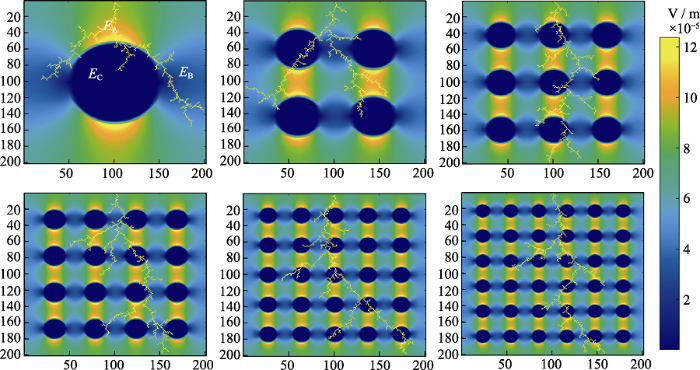
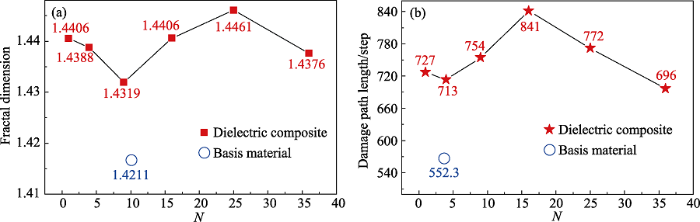
在保持无机填料体积分数一定的情况下, 分别改变其分布结构, 使用DBM模型计算得到的击穿损伤形貌如图9所示。将得到的仿真结果进行分形维数与损伤长度的计算。使用DBM模型在200×200个网格点的计算过程中, 每一步都损伤了相同的长度, 因此以计算步数作为树状损伤通道的损伤路径长度。如图10, 可以发现介电复合材料树状损伤通道的分形维数和损伤长度并没有很明显的规律, 这可能是由于DBM模型的随机特性和本研究计算程序尺度上的局限性所致。但将其与计算6次并取平均值的纯聚合物基体对比可以发现, 介电复合材料树状损伤通道的分形维数与损伤长度总是比纯基体高, 这一结果也与计算文献中纯聚合物基体和介电复合材料击穿损伤形貌的实验图像得到的结果相吻合[17]。可以看出, 纯聚合物基体虽然由于介电常数较低而无法达到高储能的目的, 但相较于介电复合材料有较高的耐击穿能力。结合图9的击穿损伤形貌可以直观得出, 这是由于添加无机填料后, 形成的介电复合材料中电场畸变对击穿损伤过程造成的影响。无机填料与基体边界处发生介电响应, 靠近无机填料且平行于电场方向的聚合物基体中的平均电场EA增强(是外加电场的几倍), 同时大于其它区域的聚合物基体局部电场EB与高介电常数的无机填料的局部电场EC (导电粒子为零), 而电击穿更容易在电场高的地方发生。因此, 击穿损伤形貌在演变时大概率向每个靠近无机填料且平行于电场方向的聚合物基体产生分支, 且距离越近概率越大, 介电复合材料的无机填料分散越均匀,击穿时演变的分支就越多。结果表明, 在进行球形填料类聚合物基复合材料的研究与制备中, 可以通过分散无机填料的方法使介电击穿的树状损伤通道的损伤位点增多, 延缓其损伤速度, 提高材料的耐击穿能力。
图9
图9
添加不同无机填料含量的介电复合材料的击穿损伤形貌
Fig. 9
Breakdown damage morphologies of dielectric composites with different contents of inorganic fillers
Colorful figures are available on website
图10
图10
不同含量无机填料的介电复合材料与纯聚合物基体的损伤形貌量化对比分析
Fig. 10
Quantitative analysis of breakdown damage morphology between dielectric composite with different contents of filler particles and pure polymer matrix
(a) Fractal dimension; (b) Damage path length
3 结论
1)无机填料与基体边界处的介电响应发生突变, 介电复合材料在填料颗粒与基体边界处电场和极化的变化很大, 会在电场方向上的相邻填料间形成集中分布的高电场区域, 从而增大其击穿损伤概率。通过使用较大介电常数的聚合物基体或较小介电常数的无机填料的方式可以减缓无机填料与基体边界处的介电差异, 继而减小其界面处高电场区域, 最终提升复合材料的耐击穿性能。
2)击穿损伤形貌在演变时大概率向每个靠近无机填料且平行于电场方向的聚合物基体产生分支, 且距离越近概率越大。保持无机填料体积分数一定时, 改变其分布结构, 使之分散得更加均匀, 介电复合材料的树状损伤通道会更容易产生分支, 从而使介电击穿时树状损伤通道的损伤位点增多, 延缓其损伤速度, 最终提升复合材料的耐击穿性能。
参考文献
Progress and perspectives in dielectric energy storage ceramics
A dielectric polymer with high electric energy density and fast discharge speed
Dielectric polymers with high dipole density have the potential to achieve very high energy density, which is required in many modern electronics and electric systems. We demonstrate that a very high energy density with fast discharge speed and low loss can be obtained in defect-modified poly(vinylidene fluoride) polymers. This is achieved by combining nonpolar and polar molecular structural changes of the polymer with the proper dielectric constants, to avoid the electric displacement saturation at electric fields well below the breakdown field. The results indicate that a very high dielectric constant may not be desirable to reach a very high energy density.
Recent advances in rational design of polymer nanocomposite dielectrics for energy storage
Electrocaloric effect in relaxor ferroelectric polymer nanocomposites for solid-state cooling
Enhanced dielectric tunability and energy storage properties of plate-like Ba0.6Sr0.4TiO3/poly(vinylidene fluoride) composites through texture arrangement
Hydrothermal synthesis of dendritic BaTiO3 ceramic powders and its application in BaTiO3/P(VDF-TrFE) composites
Ultrahigh energy density and greatly enhanced discharged efficiency of sandwich-structured polymer nanocomposites with optimized spatial organization
Fundamentals of the finite element method
Dielectric breakdown model for conductor-loaded and insulator-loaded composite materials
Fractal dimension of dielectric breakdown
Dielectric and microstructural properties of BaTiO3 and Ba0.9925Er0.0075TiO3 ceramics
Effects of particle size of dielectric fillers on the output performance of piezoelectric and triboelectric nanogenerators
Effects of dopamine- modified BaTiO3 on breakdown strength of BaTiO3/PVDF composites
Enhanced breakdown strength and energy density in PVDF nanocomposites with functionalized MgO nanoparticles
Influence of temperature on mechanical and insulation properties of epoxy-layered silicate nanocomposite
Dielectric response and tunability of a dielectric-paraelectric composite
Exploring strategies for high dielectric constant and low loss polymer dielectrics
Polymer dielectrics having high dielectric constant, high temperature capability, and low loss are attractive for a broad range of applications such as film capacitors, gate dielectrics, artificial muscles, and electrocaloric cooling. Unfortunately, it is generally observed that higher polarization or dielectric constant tends to cause significantly enhanced dielectric loss. It is therefore highly desired that the fundamental physics of all types of polarization and loss mechanisms be thoroughly understood for dielectric polymers. In this Perspective, we intend to explore advantages and disadvantages for different types of polarization. Among a number of approaches, dipolar polarization is promising for high dielectric constant and low loss polymer dielectrics, if the dipolar relaxation peak can be pushed to above the gigahertz range. In particular, dipolar glass, paraelectric, and relaxor ferroelectric polymers are discussed for the dipolar polarization approach.