电子背散射衍射(EBSD)作为一种相对较新的显微结构分析手段, 可以在较大范围内提供材料的取向、织构、相鉴定及含量分布等晶体学统计性信息^[1,2,3,4], 为无机材料制备工艺的改善、微结构调控及性能优化提供了可靠的科学依据。Fang等^[5]通过EBSD技术对梯度纳米(GNG)金属铜进行表征, 为解释其拉伸变形的机理提供了重要的显微结构证据。EBSD还是研究涂层内部残余应力分布的最佳显微结构分析手段, 为研究热障涂层的服役失效行为提供了重要支撑。EBSD提供的所有晶体学信息都依赖对菊池衍射花样的分析^[6], 菊池花样直观反映材料内部微观结构, 其中, 菊池带对应不同指数的晶面, 菊池带的交点即菊池极代表晶带轴^[4]。

相鉴定是EBSD的核心功能之一, 商用仪器主要通过匹配晶面夹角进行相鉴定, 可通过成分分析或人为预先选相来缩小相鉴定的筛选范围。需要选择的范围越小, 结果就越准确。由于只考虑晶面夹角这一种信息, 商用EBSD存在一定局限性, 有时会给出多个相鉴定结果, 甚至出现不符合材料对称性的结果, 容易产生误判。对于这种情况, 单纯依靠晶面夹角匹配难以排除, 还需对菊池花样进行对称性分析才能确定。

尽管通过菊池花样的对称性进行相鉴定具有显著优势, 可有效改善现有方法的局限性, 但目前商业仪器仍然只采用晶面夹角匹配, 主要原因在于对称轴的识别非常困难。三维空间的对称轴变成了二维平面的菊池极, 且伴随难以避免的花样畸变, 增大了判断难度。虽然一些具有明显几何特征的对称轴可直接识别, 如六次轴和二次轴, 但不具有明显特征的对称轴, 或存在与之类似的非对称轴则很难识别, 需根据对称轴的特点具体分析, 如三次轴和四次轴。根据晶体对称规律, 交于三次轴的同族晶面应呈120°旋转重合, 交于四次轴的同族晶面呈90°旋转重合。这一规律在菊池花样中表现为: 交于三次轴的同族菊池带, 其晶面夹角为120°, 交于四次轴的同族菊池带的晶面夹角为90°, 以此作为对称轴的判断依据。准确判断这类对称轴需要判断菊池带是否属于同一晶面族, 并计算它们之间的晶面夹角。

菊池带是否属于同一晶面族需计算晶面间距来判断, Dingley等^[7]尝试利用对称性进行相鉴定, 但因为晶面间距计算误差较大, 只能依靠肉眼在菊池花样中识别对称轴, 容易误判。通过菊池带宽度计算晶面间距的误差通常较大(5%~20%)^[7,8], 这是用菊池花样进行对称性分析的最大难点。我们前期工作对晶面间距进行了准确测量, 平均相对误差为2.6%^[9], 为准确识别对称轴奠定了基础, 还可区分非对称轴。对Si单晶菊池花样的分析发现了类似三次轴的非对称轴, 计算晶面间距发现, 菊池带并不属于同一晶面族, 不满足三次轴的条件, 这是肉眼识别很容易误判的。晶面夹角可通过三维空间矢量计算获得^[10], 避免了用菊池带夹角代替晶面夹角所引入的额外误差。

本研究在准确测量晶面间距的基础上, 结合对不同点群对称规律的归纳总结, 提出一种简单可行的利用菊池花样进行对称性分析的方法, 对晶体结构实现了准确判断。相较于在数据库中检索的传统相鉴定方法, 对称性分析为相鉴定提供了新思路。根据对称性排除不可能的晶体结构, 显著缩小了相鉴定范围, 还可区分常规晶面夹角匹配法无法区别的结果, 进一步提升相鉴定的可靠性, 是一种有望用于新一代EBSD设备的方法。

对于具有明显几何特征的对称轴(六次轴和二次轴), 根据其几何特征直接识别。几何特征不明显的对称轴(三次轴和四次轴)需分析交于该菊池极的菊池带。如同族菊池带的晶面夹角为120°, 判断该菊池极为三次轴; 如同族菊池带的晶面夹角为90°, 判断该菊池极为四次轴。根据计算误差, 将晶面间距和晶面夹角的容差设定为5%和1°, 即当晶面间距计算值相差在5%以内时认为属于同一晶面族, 当晶面夹角计算值相差在1°以内时认为晶面夹角相等。

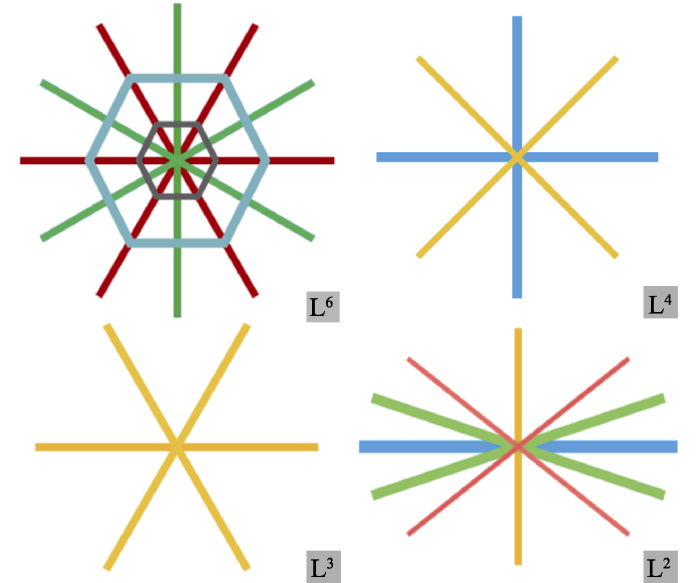
六次轴对应菊池极具有明显几何特征, 在其周围可见一个或多个由菊池带组成的六边形。四次轴对应的菊池极, 交于该菊池极的同族菊池带的晶面夹角为90°。三次轴对应的菊池极, 交于该菊池极的同族菊池带的晶面夹角为120°。二次轴也具有较为明显的几何特征, 菊池带旋转180°可以和自身重合。不同对称轴对应的菊池极如图1所示。

以上是对不同对称轴对应菊池极的简单示意, 需要结合菊池花样具体分析。

对称性是晶体分类的基础, 根据对称性晶体可分为三个晶族(Crystal category)、七个晶系(Crystal system)和32个点群(Point group)。不同的点群有各自的对称要素组合规律(对称要素包括对称轴、对称面和旋转中心等), 在菊池花样中识别出对称轴以后, 再根据这些对称轴的组合规律, 对称轴之间的夹角关系便可以进行对称性鉴定。

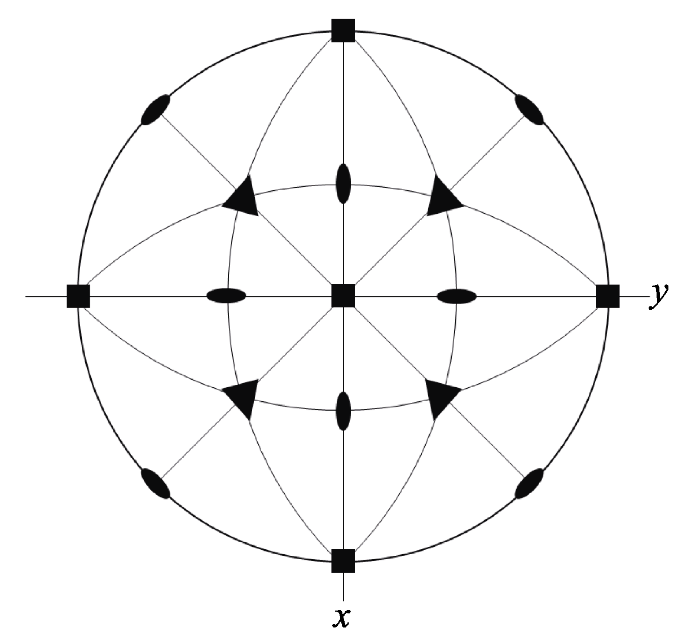
以立方晶系中的点群m3m为例说明。该点群包含三个四次轴, 四个三次轴, 六个二次轴, 九个对称面和一个对称中心。这些对称要素之间呈特定的方式组合, 对称要素之间的组合方式可用极射赤平投影图表示, m3m点群对称要素的极射赤平投影图如图2所示。

在m3m点群中, 三次轴和四次轴呈特定的空间方位组合, 它们之间的夹角只能是35.26°。不同的晶系, 不同的点群均有各自的对称特点, 且对称要素之间满足不同的组合规律, 对称轴之间的夹角关系也不同, 这是利用菊池花样进行对称性鉴定的依据。对称轴只会在晶体的特定方向出现, 例如, 六次轴只可能是六方晶系中的c轴方向, 因此可以将六次轴标定为[0001]; 再如, 在点群m3m中, 三次轴和四次轴只有一种位置关系, 四次轴可标定为[100], 三次轴可标定为[111], 而二次轴和四次轴有两种位置关系, 可标定为[110](L⁴∠L²=45°)或[011](L⁴∠L²=90°), 这是利用晶体对称性辅助标定菊池花样的思路。

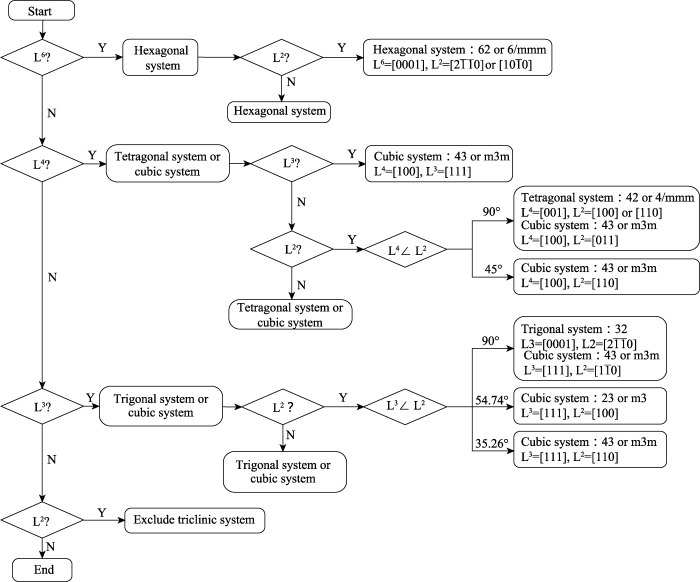
在菊池花样中识别出对称轴之后, 结合不同点群各自的对称特点, 可对花样进行对称性分析和晶体结构鉴定。受到菊池花样的制约, 不可能所有对称轴都能在花样中找到, 因此有些花样可以锁定到部分点群, 有些则只能确定到部分晶系, 而一些没有出现任何对称轴的花样则不适用于此方法。值得注意的是, 花样中未发现某种对称轴并不能说明该材料不具有该对称轴。晶体对称性鉴定流程图如图3所示。

下面是对晶体对称性鉴定准则的具体说明。

1.3.1 出现六次轴

出现六次轴可判断该晶体属六方晶系。由于六次轴不可能和三次轴、四次轴同时出现, 只需关注二次轴。如出现了二次轴则可以进一步将范围缩小到点群62和6/mmm。由于六次轴和二次轴之间只可能以90°相交, 因此无需计算两者的夹角。当然, 计算对称轴间夹角可以验证对称轴判断的准确性, 如计算发现L⁶和L²之间的夹角不为90°, 则说明对称轴的判断可能有误。

六次轴是晶体中的c轴方向, 可将六次轴的菊池极标定为[0001], 而二次轴则存在两种类型: 一种是a轴上的二次轴, 另一种则不在a轴上。这两种类型的二次轴可分别标定为[$2\bar{1}\bar{1}0$](在a轴上)和[$10\bar{1}0$](不在a轴上)。此步骤是无法区分这两种二次轴类型的。

1.3.2 出现四次轴

四次轴的出现说明该晶体为四方晶系或立方晶系。当四次轴和三次轴同时出现时该晶体必为立方晶系中的点群43或m3m。四次轴和三次轴之间的夹角只能是35.26°, 且彼此呈特定方式组合, 可将L⁴标定为[100], L³标定为[111]。

如未发现L³则接下来关注L²是否存在。L³未出现不能说明该晶体不存在三次轴, 即不能排除立方晶系的可能性。如出现L²则需要计算L⁴和L²之间的夹角。四方晶系中L⁴和L²只能以90°相交, 立方晶系中L⁴和L²的夹角可为90°或45°。当夹角为45°, 可判断为立方晶系中的点群43或m3m, 其中L⁴可标定为[100], L²可标定为[110]。当L⁴和L²的夹角为90°, 则立方和四方都有可能。为四方晶系时, 所属点群为42或4/mmm, L⁴一定是c轴方向, 可标定为[001], 而L²则有两种可能, 分别是[100](在a轴上)和[110](不在a轴上); 为立方晶系时, 点群为43或m3m, L⁴不一定为c轴方向, L⁴可标定为[100], L²可标定为[011]。

1.3.3 出现三次轴

出现三次轴可判断该晶体为三方晶系或立方晶系。如又发现了二次轴, 则可通过L³和L²的夹角进一步判断。L³和L²的夹角有三种可能性, 分别是90°、54.74°和35.26°。

当夹角为90°时, 三方和立方均有可能。该晶体可为三方晶系的点群32, 其中L³为c轴, 可标定为[0001], L²为a轴, 可标定为[$2\bar{11}0$]。该晶体也可为立方晶系中的点群43或m3m, 其中L³可标定为[111], L²则可标定为[$1\bar{1}0$]。

夹角为54.74°时只可为立方晶系, 且属于点群23或m3, 其中L³可标定为[111], L²可标定为[100]。

夹角为35.26°时, 同样只能是立方晶系, 属于点群43或m3m, L³可标定为[111], L²则标定为[110]。

1.3.4 出现二次轴

出现二次轴可排除三斜晶系。

选取三个未知样品(样品a、样品b、样品c)获取多幅菊池花样, 已知每个样品只含有一种相。通过装配在扫描电镜上的牛津EBSD系统采集菊池花样, 加速电压为20 kV。对上述三个未知样品进行对称性分析和晶体结构鉴定。根据对称轴对应菊池极的几何特征, 必要时结合菊池带夹角关系和晶面族关系, 对所获取的菊池花样中的对称轴进行了识别。对称轴之间的夹角可以通过菊池极坐标进行矢量计算获得。对称轴的识别结果如图4所示。

对这些花样分别进行分析。由于花样a1和a2属于同一相, 两者的晶体结构应一致。a1中同时出现了三次轴和二次轴, 根据图3所示的晶体对称性鉴定流程图, 可知a1属三方或立方晶系, 进一步计算三次轴和二次轴之间的夹角可将其判断为立方晶系中的点群43或m3m。a2中同时出现了四次轴和三次轴, 无需计算对称轴间夹角, 可判断为立方晶系中的点群43或m3m, 该结果与a1的判断结果相吻合。花样b1和b2中均出现了六次轴, 由此可判断样品b为六方晶系。由于没有发现其他对称轴, 无法进一步缩小范围。花样c1中出现了一个二次轴, 据此可以排除三斜晶系。花样c2则出现了六次轴, 可判断为六方晶系。虽然二次轴和六次轴并未在同一花样中同时出现, 但花样c1和c2属于同一相, 说明样品c同时含有六次轴和二次轴, 可进一步将范围缩小到六方晶系中的点群62或6/mmm。

为了进一步对结果进行验证, 本课题组通过商用EBSD获取了三个样品的相鉴定结果。样品a为点群m3m的Fe, 通过对称性分析锁定了点群43和m3m, 结果正确。样品b为点群6/mmm的SiC, 可判断其为六方晶系, 结果正确。仪器对样品c给出了多个结果: Ti-Hex(点群为6/mmm, 六方晶系)和TiBr₄(点群为2/m, 单斜晶系)。而根据对菊池花样的对称性分析可知, 样品c的菊池花样中出现了六次轴(花样c2)。根据对称定律, 六次轴的出现只可能是六方晶系, 因此可以排除仪器给出的TiBr₄这一结果。

在利用菊池花样进行对称性分析的过程中并未使用对称面等对称要素, 只用到了对称轴。根据对不同点群对称特点的分析发现, 只使用对称轴已经可以达到较好的效果, 如果引入对称面的判断, 不仅会增加判断的难度和工作量, 而且不会对结果产生较大帮助。

该方法成功应用的一个前提是花样中需要出现对称轴, 即使只出现一个对称轴也可以帮助缩小筛选范围。一般来说, 一幅花样中不会出现所有的对称轴, 这种情况下就可以用属于同一相的多幅花样进行综合分析判断。例如对样品c, 虽然二次轴和六次轴并未同时出现在一幅花样中, 但由于它们属于同一相, 说明样品c同时含有六次轴和二次轴, 这样便将范围从六方晶系进一步缩小到点群62和6/mmm。当使用属于同一相的多幅花样进行综合分析时, 还应检验不同花样得到的结果是否相互吻合。例如花样a1和a2虽然出现了不同的对称轴组合, 但最后得到的结果是一致的。

商用仪器在相鉴定过程中并未考虑晶体对称性, 依靠晶面夹角匹配从数据库中检索, 而且识别的条带数和匹配的晶面夹角数也有限, 点群为6/mmm的Ti-Hex和点群为2/m的TiBr₄两种相均能满足样品c的夹角关系, 导致出现了多个结果。它们虽然用常规的晶面夹角匹配法无法排除, 但明显不符合样品c菊池花样呈现的对称特征, 应用对称性予以排除。

晶面夹角匹配法作为目前商用EBSD相鉴定的主要方法, 适用于绝大部分材料, 具有原理简单, 快速高效的优点。但该方法往往会给出多个相鉴定结果, 甚至出现不符合材料对称性的结果, 影响了相鉴定的准确性。对称性分析可作为现有晶面夹角匹配法的重要补充, 该方法适用于出现对称轴的菊池花样, 可直接对花样进行对称性分析判断晶体结构, 显著缩小了相鉴定的筛选范围。该方法还可区分一些常规晶面夹角匹配法无法区别的结果, 从而提高相鉴定的准确性和可靠性。

本研究提出了一种利用菊池花样进行晶体结构鉴定的方法, 根据不同点群对称要素的组合规律建立了晶体对称性鉴定的流程图。运用上述方法依靠对菊池花样的分析而无需借助庞大的数据库, 成功对三个未知样品进行了对称性分析和晶体结构判断, 避免了繁重的检索工作。其中样品a判断为立方晶系中的点群43或m3m, 样品b判断属于六方晶系, 样品c判断为六方晶系中的点群62或6/mmm, 经过验证结果均正确, 并且排除了商用EBSD给出的相鉴定结果中不满足晶体对称性的结果。说明利用菊池花样进行对称性分析是判断晶体结构的有效方法, 可以显著缩小相鉴定的筛选范围, 排除不符合材料对称特点的结果。该方法可作为现有晶面夹角匹配法的重要补充, 在进行晶面夹角匹配之前先对菊池花样进行对称性分析判断晶体结构, 预先确定部分晶系或者点群, 以缩小筛选范围, 有助于获得更准确的相鉴定结果。对菊池花样的深入分析有望进一步挖掘EBSD技术在无机材料领域的应用潜力。