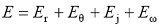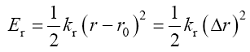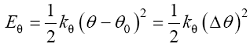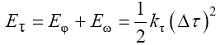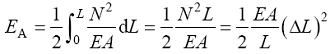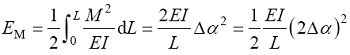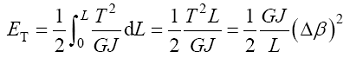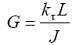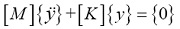石墨烯(graphene)是碳原子以共价键结合而成的一种二维晶体[1 ] , 单层石墨烯(single-layered graphene sheet, SLGS)是目前发现的最薄的层状材料, 如图1 所示。根据纳米带边缘形状不同, 石墨烯分为锯齿型(zigzag)和扶手椅型(armchair), 两者的性能也有所不同。
图1 扫描隧道显微镜下的单层石墨烯[2 ]
Fig. 1 Scanning tunneling microscope image of a SLGS[2 ]
石墨烯谐振特性涉及到纳米尺度的谐振规律, 并对谐振式传感器的未来应用有重要意义, 因此对石墨烯谐振特性进行研究十分必要。
1 石墨烯谐振特性
谐振式传感器利用敏感元件振动把被测参量转换为频率信号, 通过扫频获取谐振频率从而计算出被测参量。可见, 敏感元件材料的谐振特性对传感器性能至关重要, 常用敏感材料有硅和石英等。相比之下, 石墨烯具有更优越的力学性能和谐振特性。单层石墨烯的面内杨氏模量约为1 TPa[3 ] , 约是硅的7倍。单层石墨烯的厚度只有0.335 nm[4 ] , 远小于硅微结构能达到的厚度。石墨烯的密度约为2200 kg/m3[5 ] , 单晶硅和石英的密度约为2500 kg/m3 。尺寸为微米量级时, 硅的基频为千赫兹量级, 石墨烯的基频为兆赫兹量级。与碳纳米管相比, 石墨烯薄膜电阻低, 易于与传感器后续电路实现阻抗匹配[6 ] 。
由上可见, 石墨烯具有面内刚度大、弯曲刚度小、厚度极小、惯性质量小和谐振频率高等特点, 使用石墨烯代替现有材料作为敏感元件可望减小传感器的尺寸和功耗, 提高测量灵敏度。并且石墨烯材料对传感器等领域的影响将是变革性的, 会远大于硅代替金属、石英所带来的影响。因此很多学者研究石墨烯的谐振特性, 并使用谐振式石墨烯传感器实现单分子探测、加速度、应变和温度测量。石墨烯谐振特性的研究内容包括振动模态、谐振频率、尺寸、外力、温度和硅电极电压等因素对其谐振特性的影响, 以及提高谐振式石墨烯传感器品质因数的方法。
目前, 石墨烯谐振特性的研究方法主要包括实验测量方法和理论分析方法。理论分析方法分为基于纳米力学的分析方法和基于经典力学的分析方法, 上述方法可借助分子动力学模拟软件或有限元分析软件进行分析。
2 实验测量方法
实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] 。2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果。2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美。2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示。实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125。2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率。研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大。
图2 谐振式石墨烯传感器示意图[5 ]
Fig. 2 Schematic of a resonant graphene sensor[5 ]
图3 谐振式石墨烯传感器工作原理图[11 ]
Fig. 3 Working diagram of a resonant graphene sensor[11 ]
综上, 实验测量方法可以直接测量石墨烯谐振频率, 但是此方法对实验设备和实验条件要求较高, 比如需要保证实验环境温度稳定或谐振腔真空等。并且此方法测出的谐振频率受预应力等因素影响较大, 因此精确表征石墨烯谐振特性比较困难。目前, 实验测量方法中被测石墨烯的尺寸都在微米量级,
未见有测量1 μm以下石墨烯谐振频率的实验。这是因为制作1 μm以下石墨烯悬浮结构对工艺要求高, 并且1 μm以下石墨烯的谐振频率将达到GHz量级, 且电容量极小, 电学检测相当困难。
3 基于经典力学的分析方法
由于利用纳米力学对石墨烯谐振特性进行理论分析难度较大, 且其理论体系尚未成熟, 而经典力学理论成熟, 理论分析难度相对较小, 因此许多学者利用经典力学理论来研究石墨烯等微观结构的谐振特性。
基于经典力学的分析方法有两类: 一类利用连续介质模型模拟石墨烯; 另一类基于原子间势能的模型模拟单层石墨烯。
3.1 连续介质模型
利用连续介质模型模拟石墨烯, 是根据石墨烯很薄的特点, 采用薄膜、板、壳等连续介质模型模拟石墨烯, 然后通过Timoshenko板壳理论[13 ] 、Kirchhoff板理论[14 ] 和von Kármán薄板理论[15 ] 等分析石墨烯的力学参数和机械性能, 也可以利用ANSYS等有限元软件对构造的模型进行分析。硅、石英等材料的谐振特性一般都利用此方法进行分析。
文献[16 -19 ] 研究表明单纯利用连续介质模型模拟石墨烯计算出的谐振频率比利用分子动力学模拟或者非局部模型计算出的谐振频率大, 如图4 所示。这是因为石墨烯尺寸较小, 产生尺度效应, 并且碳原子间有晶格间距, 而经典力学理论没有考虑尺度效应和晶格间距, 因此不能将石墨烯简单地看成连续介质模型。
图4 不同方法计算出的四边固支单层石墨烯基频[17 ]
Fig. 4 Fundamental resonant frequency of a SLGS with four edges clamped calculated by different methods[17 ]
鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响。非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式。利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合。
图5 非局部板模型第一、二阶振动模态[17 ]
Fig. 5 Vibration modes of a nonlocal plate model[17 ]
也有学者利用该理论分析了表面应力等外界因素对石墨烯谐振特性的影响[24 -26 ] 。2014年, Mohammadimehr等[24 ] 利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素。同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高。2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度。也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] 。
由上可见, 采用连续介质模型方法的优点是可以不用对分子内部受力和能量进行研究, 简化计算; 缺点是板、壳等连续介质模型无法反映石墨烯晶体的晶格间距, 不能模拟出石墨烯的所有受力情况, 也无法表现出扶手椅型和锯齿型石墨烯在结构和特性方面的区别, 并且采用此种方法常常需要计算出厚度。
连续介质模型方法的研究现状是: 1)大部分使用非局部模型的研究中, 非局部参数没有经过分子动力学模拟校准, 因此适用性有限; 2)大部分采用连续介质模型分析石墨烯谐振特性的研究没有考虑外界温度等因素对谐振特性的影响。不同学者给出的模型和计算结果不尽相同, 因此能否用连续介质模型有效地计算出石墨烯谐振频率还有待探索。
3.2 基于原子间势能的模型
基于原子间势能的模型模拟单层石墨烯,是利用Cauchy-Born法则[28 -30 ] 建立微观尺度和宏观尺度变形之间的联系, 将原子受力等效为模型中的节点受力, 使原子间势能等价于连续介质的应变能, 根据原子间势能推导出连续介质单元的力学参数, 从而分析石墨烯的力学参数和机械性能。
物质是由许多原子组成的, 各原子之间以共价键相连, 把原子看作质点, 物质的变形就是由共价键拉伸、弯曲、二面角扭转和面外弯曲等相互作用的结果, 原子间势能如式(1)所示[31 -32 ] :
(1)
其中, E r 代表共价键拉伸势能, E θ 代表共价键键角弯曲势能, E ω 代表共价键二面角扭转势能, E φ 代表共价键面外扭转势能。
2003年, Li等[33 ] 首次将单层石墨烯碳原子间势能和连续介质的应变能等价, 使用均质的圆截面Euler-Bernoulli梁模拟碳-碳键, 建立了结构力学中截面刚度参数与原子间势能中力常数之间的关系。具体原理是, 在小变形假设下, 将原子间势能中的Eω 和Eφ 合并, 并采用简谐近似[34 ] , 则原子间势能可表示为:
(2)
(3)
(4)
其中, k r 、k θ 、k τ 分别键拉伸力常数、键角弯曲力常数和扭转阻力常数; ∆r 、∆θ 、∆τ 分别代表键拉伸增量、键角变化和键扭转角度变化。
根据经典结构力学理论, 长度为L 的圆截面均匀梁在受纯轴向力N 时的应变能为:
(5)
在受纯弯矩M 时的应变能为:
(6)
在受纯扭矩T 时的应变能为:
(7)
E 是杨氏模量, A 是梁横截面积, I 是惯性矩, G 是剪切模量, J 是极惯性矩, ∆L 、∆α 、∆β 分别是轴向拉伸变形、梁端部的旋转角度和梁两端的相对旋转。
将原子间势能中代表拉伸、弯曲、扭转能量的E r 、E θ 、E τ 分别与连续介质应变能中代表拉伸、弯曲、扭转能量的E A 、E M 、E T 对应;将键拉伸增量∆r 与梁轴向拉伸变形∆L 对应, 键角变化∆θ 与梁端部旋转角度2α 对应;键扭转角度变化∆τ 与梁两端相对旋转角度∆β 对应, 可得:
(8)
(9)
然后根据AMBER势[32 ] 或Morse势[35 ] 等原子间势能得到力常数k r 、k θ 、k τ , 即可计算出梁的杨氏模量E 和剪切模量G , 并对圆柱梁模型组成的石墨烯模型进行分析。
2008年, Sakhaee-Pour等[36 ] 根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 通过建立梁单元的刚度矩阵和集中质量矩阵获得了整体刚度矩阵[K ]和质量矩阵[M ], 得出了石墨烯的振动方程:
(10)
式中y 是碳原子的位移矩阵。
Sakhaee-Pour发现四边固支的单层石墨烯存在均匀应变时, 其振动基频增大, 证明使用谐振式石墨烯传感器测量应变的可能性。
2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关。文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适。也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞。
2009年, Georgantzinos等[42 ] 利用弹簧-质子模型(spring-mass model)模拟了单层石墨烯, 使用不同弹性常数的线性拉伸弹簧分别模拟碳-碳键拉伸和键角弯曲, 使用线性扭转弹簧模拟碳-碳键二面角扭转, 如图6 所示。具体原理是利用卡氏定理计算出弹簧势能与作用力的关系, 然后根据胡克定律计算出力与变形量的关系, 最终得到弹性常数。其后, 有学者对该模型进行了改进[43 -45 ] 。2014年, Kim等[44 ] 在弹簧-质子模型的基础上构造了弹性网络模型(elastic network model), 并利用粗粒化方法(coarse-graining methods)计算了石墨烯振动频率使得计算简化, 得出的石墨烯基频与实验结果吻合较好。同年, Tsiamaki等[45 ] 对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率。
图6 单层石墨烯晶胞的弹簧质子模型[42 ]
Fig. 6 Spring-mass model of a SLGS cell[42 ]
可见, 由圆柱梁构造的六边形模型利用单个圆柱梁的三种应变能模拟单个碳-碳键的三种势能, 弹簧-质子模型则利用三种弹簧的势能分别模拟单个碳-碳键的三种势能。
相比于由圆柱梁构造的六边形连续介质模型, 离散的弹簧-质子模型更符合原子间相互作用的特点, 后者还避免了碳-碳键夹角弯曲力常数等于单个圆柱梁弯曲刚度的假设, 避免了提供力常数与圆柱梁横截面积的关系。
也有学者将板模型的应变能和石墨烯的势能对应[46 -47 ] 。文献分析了石墨烯的非线性振动, 指出非线性振动与激励力大小和石墨烯尺寸有关[46 ] , 还指出将谐振式石墨烯传感器用于质量检测时, 面内张力可以调节检测灵敏度, 并且非线性振动时检测的灵敏度高于简谐振动时的灵敏度。
可见, 基于原子间势能模型的优点是可以将原子间势能与连续介质的应变能相对应, 使得构造的模型能够更符合石墨烯的微观参数, 有利于从本质上研究石墨烯特性, 弹簧-质子等模型也更体现石墨烯碳原子间的离散性, 缺点是根据此模型无法分析温度等外界条件对谐振频率的影响, 并且如果采用六边形结构模拟石墨烯晶胞, 当石墨烯尺寸达到微米量级时, 六边形数目达到几千万, 分析和计算难度较大。
基于原子间势能的模型的研究现状是: 1)少部分使用基于原子间势能的连续介质模型的研究认为石墨烯振动频率与手性无关, 这可能是因为采用的模型不能准确地反映石墨烯晶胞特性; 2)根据Euler-Bernoulli梁和Timoshenko梁计算出的圆柱梁模型的直径不同, 梁模型的直径也会略大或略小于碳原子直径。因此, 基于原子间势能的圆柱梁模型方法还需要进一步研究和改进, 才能给出准确的石墨烯的特性。3)分析石墨烯谐振特性时, 大部分采用基于原子间势能模型的研究中没有考虑预应力等因素对谐振特性的影响。
4 基于纳米力学的分析方法
基于纳米力学的分析方法分为量子力学方法、蒙特卡罗方法、分子动力学方法等, 其中分子动力学方法应用最为广泛。
量子力学可以从本质上分析材料特性, 但其理论分析比较困难, 利用计算机模拟石墨烯谐振也相当耗费资源, 因此一般采用此方法计算基本力学参数[48 -52 ] , 很少采用此方法分析谐振特性[49 ] 。
蒙特卡罗方法可以描述不同热力学条件下的原子分布组态, 但是不含动能项, 不能真实体现原子的动态变化过程。此方法使用较少, 一般只使用此方法分析石墨烯特性对温度的依赖性[53 -54 ] 。
分子动力学方法由Alder等[55 ] 提出, 已发展成为研究纳米材料力学行为和相关物理特性的重要手段。该方法能够模拟不同热力学及动力学条件下的原子分布组态, 从本质上揭示原子运动规律。
分子动力学方法将N 个粒子组成的物理系统抽象成N 个相互作用的质点, 选定N 个质点间相互作用的势函数后, 在选定的初始条件、边界条件、时间步长下, 通过求解经典牛顿动力学方程求出各个粒子的运动轨迹和速度分布, 最后根据统计理论得出系统热力学和动力学性质。分子动力学分析一般借助计算机模拟实现, 可用的模拟软件比较多, 如MS、GRPMACS、LAMMPS等。分子动力学模拟(molecular dynamics simulation, MD simulation)中常用的势函数有Morse势、Tersoff势[56 ] 、Brenner势[57 ] 、REBO势[58 ] 、AIREBO势[59 ] 等。求解牛顿运动方程的数值解法有Verlet算法、Leap-frog算法、Gear校正预测法、Velocity-Verlet算法、Beeman算法等。除了遵从牛顿定律之外, 分子动力学模拟中的粒子还需遵从系综规律。根据改变状态变量, 如粒子数N 、温度T 、压力P 和体积V 等, 系综分为微正则系综、正则系综、等温等压系综和等温等焓系综。由于原子动能与体系温度有关, 因此在恒温条件下进行的分子动力学模拟还需要对体系温度进行控制, 常用的控制温度方法有速度标度法和热浴法等。
2011年, Chowdhury等[18 ] 利用分子动力学方法和UFF力场[30 ] , 计算了不同约束条件、不同尺寸、不同弯曲模态下的扶手椅型和锯齿型单层石墨烯的谐振频率, 并与连续介质板模型得出的谐振频率进行了比较, 指出后者计算出的谐振频率偏大, 并且相对于单边固支, 双边固支时连续介质模型的谐振频率与分子动力学方法计算出的谐振频率更为接近。同年, 顾芳等[60 ] 利用分子动力学模拟和COMPASS力场分析了石墨烯谐振特性, 研究结果表明石墨烯的动态响应对手性不敏感, 尺寸与应变对石墨烯基频的影响强烈依赖于约束条件, 可以通过改变约束条件和尺寸获得谐振频率高、灵敏度高的谐振式传感器。他们还指出用四边固支型石墨烯检测单轴拉伸应变的灵敏度为7800 Hz/nanostrain, 远大于相同长度碳纳米管应变传感器的灵敏度(887 Hz/ nanostrain)[61 ] 。
2013年, Kang等[62 ] 利用分子动力学模拟和Brenner势研究了可调谐的谐振式石墨烯传感器, 通过静电激励使施加预应力的石墨烯振动, 如图7 所示。研究结果表明基频与作用在石墨烯边缘的平均张力紧密相关, 并指出谐振式石墨烯传感器适合作为超灵敏度加速度计、热传感器和质量计。
图7 谐振式石墨烯传感器示意图[62 ]
Fig. 7 Schematic of a resonant graphene sensor[62 ]
同年, 纪翔等[63 ] 使用AIREBO势、Lennard- Jones势和分子动力学模拟方法研究了有气体阻尼时石墨烯谐振频率与气体压强之间的关系, 指出气体阻尼增大, 谐振频率减小, 但气体阻尼对谐振频率影响很小。Kwon等[64 ] 利用分子动力学模拟分析了双边固支时石墨烯基频随附加质量、外力、硅电极电压的变化情况, 并指出谐振式石墨烯传感器用于质量检测时的灵敏度大约可达10-24 g。2014年, Kwon等[65 ] 又设计出十字型谐振式石墨烯传感器, 如图8 所示, 利用分子动力学模拟分析了十字型石墨烯的谐振特性, 指出可以使用该传感检测外力变化。
图8 单层十字型石墨烯分子动力学模拟图[65 ]
Fig. 8 MD simulation diagram of a cross-type SLGS[65 ]
综上, 分子动力学方法的优点是能够模拟不同热力学及动力学条件下的原子分布组态, 深入了解原子运动的复杂机制, 从本质上揭示结构运动规律。缺点是使用分子动力学模拟分析石墨烯谐振的特性计算量大, 需要使用高性能计算机; 选取不同的势函数和系综会对仿真结果产生较大影响。
5 结束语
学者们采用实验测量方法和理论分析方法研究了石墨烯谐振特性, 发现石墨烯谐振频率与形状、尺寸、厚度、约束条件、外力、外界温度、硅电极电压等因素有关。石墨烯尺寸较小时, 尺寸对石墨烯谐振频率的影响很大且成非线性关系; 边长1 nm以下、1 μm以下、1 μm以上单层石墨烯的基频大约分别是THz量级、GHz量级、MHz量级; 周边固支时石墨烯的谐振频率大于周边简支时石墨烯的谐振频率; 单轴拉伸石墨烯会增大其谐振频率; 温度降低时谐振系统的品质因数明显增大。石墨烯大幅度振动时动态响应还会呈现非线性, 这与激励石墨烯振动的外力大小有关, 且非线性振动时振动频率和灵敏度比线性振动时高。但是目前石墨烯谐振特性还没有定论, 谐振式石墨烯传感器的商业化也需要一段时间。
综上所述, 石墨烯具有优异的谐振特性, 精确表征其谐振特性具有重要意义。需对其展开进一步研究, 改善实验测量方法, 提高理论分析水平。
参考文献
文献选项
[1]
NOVOSELOV K S GEIM A K MOROZOV S V et al .Electric field effect in atomically thin carbon films
.Science , 2004 , 306 (5696 ): 666 -669 .
[本文引用: 1]
[2]
STOLYAROVA E RIM K T RYU S et al .High-resolution scanning tunneling microscopy imaging of mesoscopic graphene sheets on an insulating surface
.Proceedings of the National Academy of Sciences , 2007 , 104 (22 ): 9209 -9212 .
[本文引用: 2]
[3]
SCARPA F ADHIKARI S GIL A J et al .The bending of single layer graphene sheets: the lattice versus continuum approach
.Nanotechnology , 2010 , 21 (12 ): 125702 .
[本文引用: 1]
[4]
DRESSELHAUS M S DRESSELHAUS G SAITO R. Physics of carbon nanotubes
.Carbon , 1995 , 33 (7 ): 883 -891 .
[本文引用: 1]
[5]
BUNCH J S VAN DER ZANDE A M VERBRIDGE S S et al . Electromechanical resonators from graphene sheets
.Science , 2007 , 315 (5811 ): 490 -493 .
[本文引用: 5]
[6]
GEIM A K. Graphene: status and prospects
.Science , 2009 , 324 (5934 ): 1530 -1534 .
[本文引用: 1]
[7]
ROBINSON J T ZALALUTDINOV M BALDWIN J W et al .Wafer-scale reduced graphene oxide films for nanomechanical devices
.Nano Lett ., 2008 , 8 (10 ): 3441 -3445 .
[本文引用: 2]
[8]
HUTCHINSON A B TRUITT P A SCHWAB K C et al .Dissipation in nanocrystalline-diamond nanomechanical resonators
.Appl. Phys. Lett ., 2004 , 84 (6 ): 972 -974 .
[本文引用: 1]
[9]
SEKARIC L PARPIA J M CRAIGHEAD H G et al .Nanomechanical resonant structures in nanocrystalline diamond
.Appl. Phys. Lett ., 2002 , 81 (23 ): 4455 -4457 .
[本文引用: 1]
[10]
GARCIA-SANCHEZ D VAN DER ZANDE A M PAULO A S et al . Imaging mechanical vibrations in suspended graphene sheets
.Nano Lett ., 2008 , 8 (5 ): 1399 -1403 .
[本文引用: 1]
[11]
CHEN C ROSENBLATT S BOLOTIN K I et al .Performance of monolayer graphene nanomechanical resonators with electrical readout
.Nature Nanotech ., 2009 , 4 (12 ): 861 -867 .
[本文引用: 3]
[12]
ZANDE A M BARTON R A ALDEN J S et al .Large-scale arrays of single-layer graphene resonators
.Nano Lett ., 2010 , 10 (12 ): 4869 -4873 .
[本文引用: 2]
[13]
TIMOSHENKO S WOINOWSKY-KRIEGER S. Theory of Plates and Shells. New York: McGraw-hill , 1959 .
[本文引用: 1]
[14]
BAUCHAU O A CRAIG J I. Structural Analysis: with Applications to Aerospace Structures
. Netherlands: Springer , 2009 , 819 -821 .
[本文引用: 1]
[15]
REDDY J N. A general non-linear third-order theory of plates with moderate thickness
.Int. J. Solids Struct ., 1990 , 25 (6 ): 677 -686 .
[本文引用: 1]
[16]
MURMU T PRADHAN S C. Vibration analysis of nano-single- layered graphene sheets embedded in elastic medium based on nonlocal elasticity theory
.J. Appl. Phys ., 2009 , 105 (6 ): 064319 .
[本文引用: 2]
[17]
ARASH B WANG Q. Vibration of single-and double-layered graphene sheets
.J. Nanotechnol. Eng. Med . , 2011 , 2 (1 ): 011012 .
[本文引用: 5]
[18]
CHOWDHURY R ADHIKARI S SCARPA F et al .Transverse vibration of single-layer graphene sheets
.J. Phys. D: Appl. Phys ., 2011 , 44 (20 ): 205401 .
[本文引用: 1]
[19]
SAMAEI A T ALIHA M R M MIRSAYAR M M Frequency analysis of a graphene sheet embedded in an elastic medium with consideration of small scale
.Mater. Phys. Mech ., 2015 , 22 : 125 -135 .
[本文引用: 2]
[20]
ANSARI R SAHMANI S ARASH B. Nonlocal plate model for free vibrations of single-layered graphene sheets
.Phys. Lett. A , 2010 , 375 (1 ): 53 -62 .
[21]
SHEN L E SHEN H S ZHANG C L. Nonlocal plate model for nonlinear vibration of single layer graphene sheets in thermal environments
.Comp. Mater. Sci ., 2010 , 48 (3 ): 680 -685 .
[22]
CHANG W J LEE H L. Mass detection using a double-layer circular graphene-based nanomechanical resonator
.J. Appl. Phys ., 2014 , 116 (3 ): 034303 .
[本文引用: 1]
[23]
ERINGEN A C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves
.J. Appl. Phys ., 1983 , 54 (9 ): 4703 -4710 .
[本文引用: 1]
[24]
MOHAMMADIMEHR M NAJAFABADI M M M NASIRI H et al . Surface Stress Effects on the Free Vibration and Bending Analysis of the Nonlocal Single-layer Graphene Sheet Embedded in an Elastic Medium Using Energy Method
. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanoengineering and Nanosystems , 2014 , 1740349914559042 .
[本文引用: 2]
[25]
FAZELZADEH S A GHAVANLOO E. Nanoscale mass sensing based on vibration of single-layered graphene sheet in thermal environments
.Acta. Mech. Sinica ., 2014 , 30 (1 ): 84 -91 .
[本文引用: 1]
[26]
KARLIČIĆ D KOZIĆ P ADHIKARI S et al . Nonlocal mass-nanosensor model based on the damped vibration of single- layer graphene sheet influenced by in-plane magnetic field
.Int. J. Mech. Sci ., 2015 , 96 : 132 -142 .
[本文引用: 2]
[27]
AKGÖZ B CIVALEK Ö Free vibration analysis for single- layered graphene sheets in an elastic matrix via modified couple stress theory
.Mater. Design ., 2012 , 42 : 164 -171 .
[本文引用: 1]
[28]
TADMOR E B ORTIZ M PHILLIPS R. Quasicontinuum analysis of defects in solids
.Philos. Mag. A , 1996 , 73 (6 ): 1529 -1563 .
[本文引用: 1]
[29]
FRIESECKE G THEIL F. Convexity conditions and existence theorems in nonlinear elasticity
.J. Nonlinear Sci ., 2002 , 12 : 445 -478 .
[30]
STEINMANN P ELIZONDO A SUNYK R. Studies of validity of the Cauchy-Born rule by direct comparison of continuum and atomistic modelling
.Modell. Simul. Mater. Sci. Eng ., 2007 , 15 (1 ): S271 .
[本文引用: 2]
[31]
RAPPÉ A K CASEWIT C J COLWELL K S et al .UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations
.J. Am. Chem. Soc ., 1992 , 114 (25 ): 10024 -10035 .
[本文引用: 1]
[32]
CORNELL W D CIEPLAK P BAYLY C I et al .A second generation force field for the simulation of proteins, nucleic acids, and organic molecules
.J. Am. Chem. Soc ., 1995 , 117 : 5179 -5197 .
[本文引用: 2]
[33]
LI C CHOU T W. A structural mechanics approach for the analysis of carbon nanotubes
.Int. J. Solid Struct ., 40 (10 ): 2487 -2499 .
[本文引用: 2]
[34]
GELIN B R. Molecular Modeling of Polymer Structures and Properties
. New York: Gardner , 1994 .
[本文引用: 1]
[35]
BELYTSCHKO T XIAO S P SCHATZ G C et al .Atomistic simulations of nanotube fracture
.Phys. Rev. B , 2002 , 65 (23 ): 235430 .
[本文引用: 1]
[36]
SAKHAEE-POUR A AHMADIAN M T VAFAI A. Potential application of single-layered graphene sheet as strain sensor
.Solid State Commun ., 2008 , 147 (7 ): 336 -340 .
[本文引用: 2]
[37]
ROUHI S ANSARI R. Atomistic finite element model for axial buckling and vibration analysis of single-layered graphene sheets
.Physica E , 2012 , 44 (4 ): 764 -772 .
[本文引用: 2]
[38]
BAYKASOGLU C MUGAN A. Dynamic analysis of single-layer graphene sheets
.Comp. Mater. Sci ., 2012 , 55 : 228 -236 .
[本文引用: 1]
[39]
ODEGARD G M GATES T S WISE K E et al .Constitutive modeling of nanotube-reinforced polymer composites
.Comp. Sci. Technol ., 2003 , 63 (11 ): 1671 -1687 .
[本文引用: 1]
[40]
REDDY C D RAJENDRAN S LIEW K M. Equilibrium configuration and continuum elastic properties of finite sized graphene
.Int. J. Nanosci ., 2006 , 17 (3 ): 864 .
[41]
SCARPA F ADHIKARI S PHANI A S. Effective elastic mechanical properties of single layer graphene sheets
.Nanotechnology , 2009 , 20 (6 ): 065709 .
[本文引用: 2]
[42]
GEORGANTZINOS S K GIANNOPOULOS G I ANIFANTIS N K. An efficient numerical model for vibration analysis of single- walled carbon nanotubes
.Comput. Mech ., 2009 , 43 (6 ): 731 -741 .
[本文引用: 5]
[43]
MAHMOUDINEZHAD E ANSARI R. Vibration analysis of circular and square single-layered graphene sheets: An accurate spring mass mode
.Physica E , 2013 , 47 : 12 -16 .
[本文引用: 1]
[44]
KIM M H KIM D CHOI J B et al .Vibrational characteristics of graphene sheets elucidated using an elastic network model
.Phys. Chem. Chem. Phys ., 2014 , 16 (29 ): 15263 -15271 .
[本文引用: 2]
[45]
TSIAMAKI A S GEORGANTZINOS S K ANIFANTIS N K. Monolayer graphene resonators for mass detection: a structural mechanics feasibility study
.Sensor. Actuat. A-Phys ., 2014 , 217 : 29 -38 .
[本文引用: 2]
[46]
ATALAYA J ISACSSON A KINARET J M. Continuum elastic modeling of graphene resonators
.Nano Lett ., 2008 , 8 (12 ): 4196 -4200 .
[本文引用: 2]
[47]
DAI M D KIM C W EOM K. Nonlinear vibration behavior of graphene resonators and their applications in sensitive mass detection
.Nanoscale Res. Lett ., 2012 , 7 (1 ): 1 -10 .
[本文引用: 1]
[48]
VAN LIER G VAN ALSENOY C VAN DOREN V et al .Ab initio study of the elastic properties of single-walled carbon nanotubes and graphene
. Chem.Phys. Lett ., 2000 , 326 (1 ): 181 -185 .
[本文引用: 1]
[49]
Kudin K N Scuseria G E Yakobson B I. C2 F, BN, and C nanoshell elasticity from ab initio computations
.Phys. Rev. B , 2001 , 64 (23 ): 235406 .
[本文引用: 1]
[50]
LIU F MING P LI J. Ab initio calculation of ideal strength and phonon instability of graphene under tension
.Phys. Rev. B , 2007 , 76 (6 ): 064120 .
[51]
GAO Y HAO P. Mechanical properties of monolayer graphene under tensile and compressive loading
.Physica E , 2009 , 41 (8 ): 1561 -1566 .
[52]
RASULI R AHADIAN M M. Mechanical properties of graphene cantilever from atomic force microscopy and density functional theory
.Nanotechnology , 2010 , 21 (18 ): 185503 .
[本文引用: 1]
[53]
ZAKHARCHENKO K V KATSNELSON M I FASOLINO A. Finite temperature lattice properties of graphene beyond the quasiharmonic approximation
.Phys. Rev. Lett ., 2009 , 102 (4 ): 046808 .
[本文引用: 1]
[54]
CHEN S CHRZAN D C. Monte Carlo simulation of temperature- dependent elastic properties of graphene
.Phys. Rev. B , 2011 , 84 (19 ): 195409 .
[本文引用: 1]
[55]
ALDER B J WAINWRIGHT T E. Phase transition for a hard sphere system
.J. Chem. Phys ., 1957 , 27 (5 ): 1208 .
[本文引用: 1]
[56]
TERSOFF J. New empirical approach for the structure and energy of covalent systems
.Phys. Rev. B , 1988 , 37 (12 ): 6991 .
[本文引用: 1]
[57]
BRENNER D W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films
.Phys. Rev. B , 1990 , 42 (15 ): 9458 .
[本文引用: 1]
[58]
BRENNER D W SHENDEROVA O A HARRISON J A et al .A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons
.J. Phys.: Condens. Matter ., 2002 , 14 (4 ): 783 .
[本文引用: 1]
[59]
STUART S J TUTEIN A B HARRISON J A. A reactive potential for hydrocarbons with intermolecular interactions
.J. Chem. Phys ., 2000 , 112 (14 ): 6472 -6486 .
[本文引用: 1]
[60]
GU F ZHANG J H YANG L J et al . Molecular dynamics simulation of resonance properties of strain graphene nanoribbons
. Acta Phys. Sin ., 2011 , 60 (5 ): 523 -531 .
[本文引用: 1]
[61]
LI Y QIU X M YANG F et al .Ultra-high sensitivity of super carbon-nanotube-based mass and strain sensors
.Nanotechnology , 2008 , 19 (16 ): 165502 .
[本文引用: 1]
[62]
KANG J W KIM H W KIM K S et al .Molecular dynamics modeling and simulation of a graphene-based nanoelectromechanical resonator
.Curr. Appl. Phys ., 2013 , 13 (4 ): 789 -794 .
[本文引用: 3]
[63]
纪翔 . 石墨烯纳米带谐振特性的基础研究
. 西安: 西安电子科技大学 , 2013 .
[本文引用: 1]
[64]
KWON O K KIM K S PARK J et al .Molecular dynamics modeling and simulations of graphene-nanoribbon-resonator-based nanobalance as yoctogram resolution detector
.Comp. Mater. Sci ., 2013 , 67 : 329 -333 .
[本文引用: 1]
[65]
KWON , OH KUEN HO JUNG HWANG et al . Molecular dynamics simulation study on cross-type graphene resonator
. Comp. Mater. Sci ., 2014 , 82 : 280 -285 .
[本文引用: 3]
Electric field effect in atomically thin carbon films
1
2004
... 石墨烯(graphene)是碳原子以共价键结合而成的一种二维晶体[1 ] , 单层石墨烯(single-layered graphene sheet, SLGS)是目前发现的最薄的层状材料, 如图1 所示.根据纳米带边缘形状不同, 石墨烯分为锯齿型(zigzag)和扶手椅型(armchair), 两者的性能也有所不同. ...
High-resolution scanning tunneling microscopy imaging of mesoscopic graphene sheets on an insulating surface
2
2007
... 扫描隧道显微镜下的单层石墨烯[2 ] ...
... Scanning tunneling microscope image of a SLGS[2 ] ...
The bending of single layer graphene sheets: the lattice versus continuum approach
1
2010
... 谐振式传感器利用敏感元件振动把被测参量转换为频率信号, 通过扫频获取谐振频率从而计算出被测参量.可见, 敏感元件材料的谐振特性对传感器性能至关重要, 常用敏感材料有硅和石英等.相比之下, 石墨烯具有更优越的力学性能和谐振特性.单层石墨烯的面内杨氏模量约为1 TPa[3 ] , 约是硅的7倍.单层石墨烯的厚度只有0.335 nm[4 ] , 远小于硅微结构能达到的厚度.石墨烯的密度约为2200 kg/m3[5 ] , 单晶硅和石英的密度约为2500 kg/m3 .尺寸为微米量级时, 硅的基频为千赫兹量级, 石墨烯的基频为兆赫兹量级.与碳纳米管相比, 石墨烯薄膜电阻低, 易于与传感器后续电路实现阻抗匹配[6 ] . ...
Physics of carbon nanotubes
1
1995
... 谐振式传感器利用敏感元件振动把被测参量转换为频率信号, 通过扫频获取谐振频率从而计算出被测参量.可见, 敏感元件材料的谐振特性对传感器性能至关重要, 常用敏感材料有硅和石英等.相比之下, 石墨烯具有更优越的力学性能和谐振特性.单层石墨烯的面内杨氏模量约为1 TPa[3 ] , 约是硅的7倍.单层石墨烯的厚度只有0.335 nm[4 ] , 远小于硅微结构能达到的厚度.石墨烯的密度约为2200 kg/m3[5 ] , 单晶硅和石英的密度约为2500 kg/m3 .尺寸为微米量级时, 硅的基频为千赫兹量级, 石墨烯的基频为兆赫兹量级.与碳纳米管相比, 石墨烯薄膜电阻低, 易于与传感器后续电路实现阻抗匹配[6 ] . ...
Electromechanical resonators from graphene sheets
5
2007
... 谐振式传感器利用敏感元件振动把被测参量转换为频率信号, 通过扫频获取谐振频率从而计算出被测参量.可见, 敏感元件材料的谐振特性对传感器性能至关重要, 常用敏感材料有硅和石英等.相比之下, 石墨烯具有更优越的力学性能和谐振特性.单层石墨烯的面内杨氏模量约为1 TPa[3 ] , 约是硅的7倍.单层石墨烯的厚度只有0.335 nm[4 ] , 远小于硅微结构能达到的厚度.石墨烯的密度约为2200 kg/m3[5 ] , 单晶硅和石英的密度约为2500 kg/m3 .尺寸为微米量级时, 硅的基频为千赫兹量级, 石墨烯的基频为兆赫兹量级.与碳纳米管相比, 石墨烯薄膜电阻低, 易于与传感器后续电路实现阻抗匹配[6 ] . ...
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
... [5 ]制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
... 谐振式石墨烯传感器示意图[5 ] ...
... Schematic of a resonant graphene sensor[5 ] ...
Graphene: status and prospects
1
2009
... 谐振式传感器利用敏感元件振动把被测参量转换为频率信号, 通过扫频获取谐振频率从而计算出被测参量.可见, 敏感元件材料的谐振特性对传感器性能至关重要, 常用敏感材料有硅和石英等.相比之下, 石墨烯具有更优越的力学性能和谐振特性.单层石墨烯的面内杨氏模量约为1 TPa[3 ] , 约是硅的7倍.单层石墨烯的厚度只有0.335 nm[4 ] , 远小于硅微结构能达到的厚度.石墨烯的密度约为2200 kg/m3[5 ] , 单晶硅和石英的密度约为2500 kg/m3 .尺寸为微米量级时, 硅的基频为千赫兹量级, 石墨烯的基频为兆赫兹量级.与碳纳米管相比, 石墨烯薄膜电阻低, 易于与传感器后续电路实现阻抗匹配[6 ] . ...
Wafer-scale reduced graphene oxide films for nanomechanical devices
2
2008
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
... [7 ]制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
Dissipation in nanocrystalline-diamond nanomechanical resonators
1
2004
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
Nanomechanical resonant structures in nanocrystalline diamond
1
2002
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
Imaging mechanical vibrations in suspended graphene sheets
1
2008
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
Performance of monolayer graphene nanomechanical resonators with electrical readout
3
2009
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
... 谐振式石墨烯传感器工作原理图[11 ] ...
... Working diagram of a resonant graphene sensor[11 ] ...
Large-scale arrays of single-layer graphene resonators
2
2010
... 实验测量方法通过电激励、光激励等方法使石墨烯振动, 直接测量其谐振频率[5 ,7 ,10 -12 ] .2007年, Bunch等[5 ] 制作了谐振式石墨烯传感器, 如图2 所示, 分析了双边固支的单层和多层石墨烯的谐振特性, 测得双边固支的单层石墨烯基频为70.5 MHz, 比将石墨烯视为梁计算出的频率要大得多, 并认为这是由于双边固支时石墨烯存在预应力的结果.2008年, Robinson等[7 ] 制作了谐振式氧化石墨烯膜传感器, 发现其品质因数普遍大于1500, 最高可以达到4000, 可以与室温下品质因数为3000的谐振式钻石传感器[8 -9 ] 相媲美.2009年, Chen等[11 ] 制作了谐振式石墨烯传感器及其后续处理电路, 通过静电激励使石墨烯振动, 工作原理图如图3 所示.实验发现石墨烯谐振频率与硅电极电压、外界温度和附加质量有关, 测得长宽分别为1.1 μm和3.3 μm的单层石墨烯的谐振频率是65 MHz, 品质因数为125.2010年, Zande等[12 ] 利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
... [12 ]利用化学气相沉积技术制作了谐振式石墨烯传感器, 使用光激励和电检测方法测定了双边固支和四边固支石墨烯的谐振频率.研究结果表明可以使用化学气相沉积技术大量生产具有相同优良电气性能和机械性能的石墨烯阵列, 并且发现石墨烯谐振频率与温度有关, 温度降低时品质因数明显增大. ...
1
1959
... 利用连续介质模型模拟石墨烯, 是根据石墨烯很薄的特点, 采用薄膜、板、壳等连续介质模型模拟石墨烯, 然后通过Timoshenko板壳理论[13 ] 、Kirchhoff板理论[14 ] 和von Kármán薄板理论[15 ] 等分析石墨烯的力学参数和机械性能, 也可以利用ANSYS等有限元软件对构造的模型进行分析.硅、石英等材料的谐振特性一般都利用此方法进行分析. ...
Structural Analysis: with Applications to Aerospace Structures
1
2009
... 利用连续介质模型模拟石墨烯, 是根据石墨烯很薄的特点, 采用薄膜、板、壳等连续介质模型模拟石墨烯, 然后通过Timoshenko板壳理论[13 ] 、Kirchhoff板理论[14 ] 和von Kármán薄板理论[15 ] 等分析石墨烯的力学参数和机械性能, 也可以利用ANSYS等有限元软件对构造的模型进行分析.硅、石英等材料的谐振特性一般都利用此方法进行分析. ...
A general non-linear third-order theory of plates with moderate thickness
1
1990
... 利用连续介质模型模拟石墨烯, 是根据石墨烯很薄的特点, 采用薄膜、板、壳等连续介质模型模拟石墨烯, 然后通过Timoshenko板壳理论[13 ] 、Kirchhoff板理论[14 ] 和von Kármán薄板理论[15 ] 等分析石墨烯的力学参数和机械性能, 也可以利用ANSYS等有限元软件对构造的模型进行分析.硅、石英等材料的谐振特性一般都利用此方法进行分析. ...
Vibration analysis of nano-single- layered graphene sheets embedded in elastic medium based on nonlocal elasticity theory
2
2009
... 文献[16 -19 ] 研究表明单纯利用连续介质模型模拟石墨烯计算出的谐振频率比利用分子动力学模拟或者非局部模型计算出的谐振频率大, 如图4 所示.这是因为石墨烯尺寸较小, 产生尺度效应, 并且碳原子间有晶格间距, 而经典力学理论没有考虑尺度效应和晶格间距, 因此不能将石墨烯简单地看成连续介质模型. ...
... 鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响.非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式.利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合. ...
Vibration of single-and double-layered graphene sheets
5
2011
... 不同方法计算出的四边固支单层石墨烯基频[17 ] ...
... Fundamental resonant frequency of a SLGS with four edges clamped calculated by different methods[17 ] ...
... 鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响.非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式.利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合. ...
... 非局部板模型第一、二阶振动模态[17 ] ...
... Vibration modes of a nonlocal plate model[17 ]
Transverse vibration of single-layer graphene sheets
1
2011
... 2011年, Chowdhury等[18 ] 利用分子动力学方法和UFF力场[30 ] , 计算了不同约束条件、不同尺寸、不同弯曲模态下的扶手椅型和锯齿型单层石墨烯的谐振频率, 并与连续介质板模型得出的谐振频率进行了比较, 指出后者计算出的谐振频率偏大, 并且相对于单边固支, 双边固支时连续介质模型的谐振频率与分子动力学方法计算出的谐振频率更为接近.同年, 顾芳等[60 ] 利用分子动力学模拟和COMPASS力场分析了石墨烯谐振特性, 研究结果表明石墨烯的动态响应对手性不敏感, 尺寸与应变对石墨烯基频的影响强烈依赖于约束条件, 可以通过改变约束条件和尺寸获得谐振频率高、灵敏度高的谐振式传感器.他们还指出用四边固支型石墨烯检测单轴拉伸应变的灵敏度为7800 Hz/nanostrain, 远大于相同长度碳纳米管应变传感器的灵敏度(887 Hz/ nanostrain)[61 ] . ...
Frequency analysis of a graphene sheet embedded in an elastic medium with consideration of small scale
2
2015
... 文献[16 -19 ] 研究表明单纯利用连续介质模型模拟石墨烯计算出的谐振频率比利用分子动力学模拟或者非局部模型计算出的谐振频率大, 如图4 所示.这是因为石墨烯尺寸较小, 产生尺度效应, 并且碳原子间有晶格间距, 而经典力学理论没有考虑尺度效应和晶格间距, 因此不能将石墨烯简单地看成连续介质模型. ...
... 鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响.非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式.利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合. ...
Nonlocal plate model for free vibrations of single-layered graphene sheets
0
2010
Nonlocal plate model for nonlinear vibration of single layer graphene sheets in thermal environments
0
2010
Mass detection using a double-layer circular graphene-based nanomechanical resonator
1
2014
... 鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响.非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式.利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合. ...
On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves
1
1983
... 鉴于此, 有学者[16 -17 ,19 -22 ] 利用Eringe提出的非局部弹性理论[23 ] (nonlocal elasticity theory)来处理使用连续介质模型时尺度效应的影响.非局部弹性理论的基本思想是一个参考点上的应力不仅取决于此点的应变, 也取决于其他每个点的应变, 非局部参数取决于石墨烯的约束条件和振动模式.利用非局部弹性理论可以求出石墨烯振动模态和谐振频率, 如图5 所示, 并且求出的谐振频率与实验数据基本吻合. ...
Surface Stress Effects on the Free Vibration and Bending Analysis of the Nonlocal Single-layer Graphene Sheet Embedded in an Elastic Medium Using Energy Method
2
2014
... 也有学者利用该理论分析了表面应力等外界因素对石墨烯谐振特性的影响[24 -26 ] .2014年, Mohammadimehr等[24 ] 利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素.同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高.2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
... [24 ]利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素.同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高.2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
Nanoscale mass sensing based on vibration of single-layered graphene sheet in thermal environments
1
2014
... 也有学者利用该理论分析了表面应力等外界因素对石墨烯谐振特性的影响[24 -26 ] .2014年, Mohammadimehr等[24 ] 利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素.同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高.2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
Nonlocal mass-nanosensor model based on the damped vibration of single- layer graphene sheet influenced by in-plane magnetic field
2
2015
... 也有学者利用该理论分析了表面应力等外界因素对石墨烯谐振特性的影响[24 -26 ] .2014年, Mohammadimehr等[24 ] 利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素.同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高.2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
... [26 ]根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
Free vibration analysis for single- layered graphene sheets in an elastic matrix via modified couple stress theory
1
2012
... 也有学者利用该理论分析了表面应力等外界因素对石墨烯谐振特性的影响[24 -26 ] .2014年, Mohammadimehr等[24 ] 利用非局部弹性理论和能量法分析了表面应力对嵌入弹性介质中石墨烯振动的影响, 发现石墨烯振动频率随表面残余应力增大而减小, 随表面层材料密度和杨氏模量增加而增加, 认为表面应力是影响石墨烯尺度效应相关特性最重要的因素.同年, Fazelzadeh等[25 ] 利用石墨烯谐振特性设计了纳米尺度的质量传感器, 借助非局部板模型和Galerkin有限元法获得了石墨烯谐振频率和相对频率偏移公式, 并分析了附加质量和外界温度变化对谐振频移的影响, 指出当附加的纳米粒子靠近石墨烯薄膜中心时, 谐振频率减小, 相对频移增大;当温差增大时, 相对频移增大, 传感器灵敏度提高.2015年, Karličić等[26 ] 根据非局部弹性理论和石墨烯谐振特性设计了平面磁场下的谐振式质量传感器, 指出磁场可有效提高传感器的灵敏度.也有学者使用修正的偶应力理论来解决尺度效应问题, 该理论考虑了结构内部尺寸的影响[27 ] . ...
Quasicontinuum analysis of defects in solids
1
1996
... 基于原子间势能的模型模拟单层石墨烯,是利用Cauchy-Born法则[28 -30 ] 建立微观尺度和宏观尺度变形之间的联系, 将原子受力等效为模型中的节点受力, 使原子间势能等价于连续介质的应变能, 根据原子间势能推导出连续介质单元的力学参数, 从而分析石墨烯的力学参数和机械性能. ...
Convexity conditions and existence theorems in nonlinear elasticity
0
2002
Studies of validity of the Cauchy-Born rule by direct comparison of continuum and atomistic modelling
2
2007
... 基于原子间势能的模型模拟单层石墨烯,是利用Cauchy-Born法则[28 -30 ] 建立微观尺度和宏观尺度变形之间的联系, 将原子受力等效为模型中的节点受力, 使原子间势能等价于连续介质的应变能, 根据原子间势能推导出连续介质单元的力学参数, 从而分析石墨烯的力学参数和机械性能. ...
... 2011年, Chowdhury等[18 ] 利用分子动力学方法和UFF力场[30 ] , 计算了不同约束条件、不同尺寸、不同弯曲模态下的扶手椅型和锯齿型单层石墨烯的谐振频率, 并与连续介质板模型得出的谐振频率进行了比较, 指出后者计算出的谐振频率偏大, 并且相对于单边固支, 双边固支时连续介质模型的谐振频率与分子动力学方法计算出的谐振频率更为接近.同年, 顾芳等[60 ] 利用分子动力学模拟和COMPASS力场分析了石墨烯谐振特性, 研究结果表明石墨烯的动态响应对手性不敏感, 尺寸与应变对石墨烯基频的影响强烈依赖于约束条件, 可以通过改变约束条件和尺寸获得谐振频率高、灵敏度高的谐振式传感器.他们还指出用四边固支型石墨烯检测单轴拉伸应变的灵敏度为7800 Hz/nanostrain, 远大于相同长度碳纳米管应变传感器的灵敏度(887 Hz/ nanostrain)[61 ] . ...
UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations
1
1992
... 物质是由许多原子组成的, 各原子之间以共价键相连, 把原子看作质点, 物质的变形就是由共价键拉伸、弯曲、二面角扭转和面外弯曲等相互作用的结果, 原子间势能如式(1)所示[31 -32 ] : ...
A second generation force field for the simulation of proteins, nucleic acids, and organic molecules
2
1995
... 物质是由许多原子组成的, 各原子之间以共价键相连, 把原子看作质点, 物质的变形就是由共价键拉伸、弯曲、二面角扭转和面外弯曲等相互作用的结果, 原子间势能如式(1)所示[31 -32 ] : ...
... 然后根据AMBER势[32 ] 或Morse势[35 ] 等原子间势能得到力常数k r 、k θ 、k τ , 即可计算出梁的杨氏模量E 和剪切模量G , 并对圆柱梁模型组成的石墨烯模型进行分析. ...
A structural mechanics approach for the analysis of carbon nanotubes
2
... 2003年, Li等[33 ] 首次将单层石墨烯碳原子间势能和连续介质的应变能等价, 使用均质的圆截面Euler-Bernoulli梁模拟碳-碳键, 建立了结构力学中截面刚度参数与原子间势能中力常数之间的关系.具体原理是, 在小变形假设下, 将原子间势能中的Eω 和Eφ 合并, 并采用简谐近似[34 ] , 则原子间势能可表示为: ...
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
Molecular Modeling of Polymer Structures and Properties
1
1994
... 2003年, Li等[33 ] 首次将单层石墨烯碳原子间势能和连续介质的应变能等价, 使用均质的圆截面Euler-Bernoulli梁模拟碳-碳键, 建立了结构力学中截面刚度参数与原子间势能中力常数之间的关系.具体原理是, 在小变形假设下, 将原子间势能中的Eω 和Eφ 合并, 并采用简谐近似[34 ] , 则原子间势能可表示为: ...
Atomistic simulations of nanotube fracture
1
2002
... 然后根据AMBER势[32 ] 或Morse势[35 ] 等原子间势能得到力常数k r 、k θ 、k τ , 即可计算出梁的杨氏模量E 和剪切模量G , 并对圆柱梁模型组成的石墨烯模型进行分析. ...
Potential application of single-layered graphene sheet as strain sensor
2
2008
... 2008年, Sakhaee-Pour等[36 ] 根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 通过建立梁单元的刚度矩阵和集中质量矩阵获得了整体刚度矩阵[K ]和质量矩阵[M ], 得出了石墨烯的振动方程: ...
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
Atomistic finite element model for axial buckling and vibration analysis of single-layered graphene sheets
2
2012
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
... -37 ]中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
Dynamic analysis of single-layer graphene sheets
1
2012
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
Constitutive modeling of nanotube-reinforced polymer composites
1
2003
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
Equilibrium configuration and continuum elastic properties of finite sized graphene
0
2006
Effective elastic mechanical properties of single layer graphene sheets
2
2009
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
... [41 ]或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
An efficient numerical model for vibration analysis of single- walled carbon nanotubes
5
2009
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
... 2009年, Georgantzinos等[42 ] 利用弹簧-质子模型(spring-mass model)模拟了单层石墨烯, 使用不同弹性常数的线性拉伸弹簧分别模拟碳-碳键拉伸和键角弯曲, 使用线性扭转弹簧模拟碳-碳键二面角扭转, 如图6 所示.具体原理是利用卡氏定理计算出弹簧势能与作用力的关系, 然后根据胡克定律计算出力与变形量的关系, 最终得到弹性常数.其后, 有学者对该模型进行了改进[43 -45 ] .2014年, Kim等[44 ] 在弹簧-质子模型的基础上构造了弹性网络模型(elastic network model), 并利用粗粒化方法(coarse-graining methods)计算了石墨烯振动频率使得计算简化, 得出的石墨烯基频与实验结果吻合较好.同年, Tsiamaki等[45 ] 对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
... [42 ]中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
... 单层石墨烯晶胞的弹簧质子模型[42 ] ...
... Spring-mass model of a SLGS cell[42 ] ...
Vibration analysis of circular and square single-layered graphene sheets: An accurate spring mass mode
1
2013
... 2009年, Georgantzinos等[42 ] 利用弹簧-质子模型(spring-mass model)模拟了单层石墨烯, 使用不同弹性常数的线性拉伸弹簧分别模拟碳-碳键拉伸和键角弯曲, 使用线性扭转弹簧模拟碳-碳键二面角扭转, 如图6 所示.具体原理是利用卡氏定理计算出弹簧势能与作用力的关系, 然后根据胡克定律计算出力与变形量的关系, 最终得到弹性常数.其后, 有学者对该模型进行了改进[43 -45 ] .2014年, Kim等[44 ] 在弹簧-质子模型的基础上构造了弹性网络模型(elastic network model), 并利用粗粒化方法(coarse-graining methods)计算了石墨烯振动频率使得计算简化, 得出的石墨烯基频与实验结果吻合较好.同年, Tsiamaki等[45 ] 对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
Vibrational characteristics of graphene sheets elucidated using an elastic network model
2
2014
... 2012年, Rouhi等[37 ] 也根据Li提出的圆柱梁模型构建了六边形结构模拟石墨烯晶胞, 计算了不同长宽比、不同约束条件下石墨烯的振动频率, 发现石墨烯基频与手性和长宽比几乎无关.文献[33 ,36 -37 ] 中使用的梁是Euler-Bernoull梁, 忽略了梁的剪切变形, 但是通常细长梁才能忽略剪切变形, 根据碳-碳键长和圆柱横截面直径的关系, 模拟碳-碳键的圆柱梁不是细长梁, 因此使用文献[38 ] 中的Timoshenko梁比较合适.也有学者使用桁架模型[39 -41 ] 、蜂窝模型[41 ] 或弹簧-质子模型[42 -44 ] 模拟石墨烯晶胞. ...
... 2009年, Georgantzinos等[42 ] 利用弹簧-质子模型(spring-mass model)模拟了单层石墨烯, 使用不同弹性常数的线性拉伸弹簧分别模拟碳-碳键拉伸和键角弯曲, 使用线性扭转弹簧模拟碳-碳键二面角扭转, 如图6 所示.具体原理是利用卡氏定理计算出弹簧势能与作用力的关系, 然后根据胡克定律计算出力与变形量的关系, 最终得到弹性常数.其后, 有学者对该模型进行了改进[43 -45 ] .2014年, Kim等[44 ] 在弹簧-质子模型的基础上构造了弹性网络模型(elastic network model), 并利用粗粒化方法(coarse-graining methods)计算了石墨烯振动频率使得计算简化, 得出的石墨烯基频与实验结果吻合较好.同年, Tsiamaki等[45 ] 对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
Monolayer graphene resonators for mass detection: a structural mechanics feasibility study
2
2014
... 2009年, Georgantzinos等[42 ] 利用弹簧-质子模型(spring-mass model)模拟了单层石墨烯, 使用不同弹性常数的线性拉伸弹簧分别模拟碳-碳键拉伸和键角弯曲, 使用线性扭转弹簧模拟碳-碳键二面角扭转, 如图6 所示.具体原理是利用卡氏定理计算出弹簧势能与作用力的关系, 然后根据胡克定律计算出力与变形量的关系, 最终得到弹性常数.其后, 有学者对该模型进行了改进[43 -45 ] .2014年, Kim等[44 ] 在弹簧-质子模型的基础上构造了弹性网络模型(elastic network model), 并利用粗粒化方法(coarse-graining methods)计算了石墨烯振动频率使得计算简化, 得出的石墨烯基频与实验结果吻合较好.同年, Tsiamaki等[45 ] 对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
... [45 ]对弹簧-质子模型[42 ] 中对应键角弯曲的拉伸弹簧的参数进行了优化, 并且采用弹簧模拟了碳-碳键面外扭转而不是二面角扭转, 计算出圆形单层石墨烯弯曲模态和面内模态的振动频率. ...
Continuum elastic modeling of graphene resonators
2
2008
... 也有学者将板模型的应变能和石墨烯的势能对应[46 -47 ] .文献分析了石墨烯的非线性振动, 指出非线性振动与激励力大小和石墨烯尺寸有关[46 ] , 还指出将谐振式石墨烯传感器用于质量检测时, 面内张力可以调节检测灵敏度, 并且非线性振动时检测的灵敏度高于简谐振动时的灵敏度. ...
... [46 ], 还指出将谐振式石墨烯传感器用于质量检测时, 面内张力可以调节检测灵敏度, 并且非线性振动时检测的灵敏度高于简谐振动时的灵敏度. ...
Nonlinear vibration behavior of graphene resonators and their applications in sensitive mass detection
1
2012
... 也有学者将板模型的应变能和石墨烯的势能对应[46 -47 ] .文献分析了石墨烯的非线性振动, 指出非线性振动与激励力大小和石墨烯尺寸有关[46 ] , 还指出将谐振式石墨烯传感器用于质量检测时, 面内张力可以调节检测灵敏度, 并且非线性振动时检测的灵敏度高于简谐振动时的灵敏度. ...
Ab initio study of the elastic properties of single-walled carbon nanotubes and graphene
1
2000
... 量子力学可以从本质上分析材料特性, 但其理论分析比较困难, 利用计算机模拟石墨烯谐振也相当耗费资源, 因此一般采用此方法计算基本力学参数[48 -52 ] , 很少采用此方法分析谐振特性[49 ] . ...
C2 F, BN, and C nanoshell elasticity from ab initio computations
1
2001
... 量子力学可以从本质上分析材料特性, 但其理论分析比较困难, 利用计算机模拟石墨烯谐振也相当耗费资源, 因此一般采用此方法计算基本力学参数[48 -52 ] , 很少采用此方法分析谐振特性[49 ] . ...
Ab initio calculation of ideal strength and phonon instability of graphene under tension
0
2007
Mechanical properties of monolayer graphene under tensile and compressive loading
0
2009
Mechanical properties of graphene cantilever from atomic force microscopy and density functional theory
1
2010
... 量子力学可以从本质上分析材料特性, 但其理论分析比较困难, 利用计算机模拟石墨烯谐振也相当耗费资源, 因此一般采用此方法计算基本力学参数[48 -52 ] , 很少采用此方法分析谐振特性[49 ] . ...
Finite temperature lattice properties of graphene beyond the quasiharmonic approximation
1
2009
... 蒙特卡罗方法可以描述不同热力学条件下的原子分布组态, 但是不含动能项, 不能真实体现原子的动态变化过程.此方法使用较少, 一般只使用此方法分析石墨烯特性对温度的依赖性[53 -54 ] . ...
Monte Carlo simulation of temperature- dependent elastic properties of graphene
1
2011
... 蒙特卡罗方法可以描述不同热力学条件下的原子分布组态, 但是不含动能项, 不能真实体现原子的动态变化过程.此方法使用较少, 一般只使用此方法分析石墨烯特性对温度的依赖性[53 -54 ] . ...
Phase transition for a hard sphere system
1
1957
... 分子动力学方法由Alder等[55 ] 提出, 已发展成为研究纳米材料力学行为和相关物理特性的重要手段.该方法能够模拟不同热力学及动力学条件下的原子分布组态, 从本质上揭示原子运动规律. ...
New empirical approach for the structure and energy of covalent systems
1
1988
... 分子动力学方法将N 个粒子组成的物理系统抽象成N 个相互作用的质点, 选定N 个质点间相互作用的势函数后, 在选定的初始条件、边界条件、时间步长下, 通过求解经典牛顿动力学方程求出各个粒子的运动轨迹和速度分布, 最后根据统计理论得出系统热力学和动力学性质.分子动力学分析一般借助计算机模拟实现, 可用的模拟软件比较多, 如MS、GRPMACS、LAMMPS等.分子动力学模拟(molecular dynamics simulation, MD simulation)中常用的势函数有Morse势、Tersoff势[56 ] 、Brenner势[57 ] 、REBO势[58 ] 、AIREBO势[59 ] 等.求解牛顿运动方程的数值解法有Verlet算法、Leap-frog算法、Gear校正预测法、Velocity-Verlet算法、Beeman算法等.除了遵从牛顿定律之外, 分子动力学模拟中的粒子还需遵从系综规律.根据改变状态变量, 如粒子数N 、温度T 、压力P 和体积V 等, 系综分为微正则系综、正则系综、等温等压系综和等温等焓系综.由于原子动能与体系温度有关, 因此在恒温条件下进行的分子动力学模拟还需要对体系温度进行控制, 常用的控制温度方法有速度标度法和热浴法等. ...
Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films
1
1990
... 分子动力学方法将N 个粒子组成的物理系统抽象成N 个相互作用的质点, 选定N 个质点间相互作用的势函数后, 在选定的初始条件、边界条件、时间步长下, 通过求解经典牛顿动力学方程求出各个粒子的运动轨迹和速度分布, 最后根据统计理论得出系统热力学和动力学性质.分子动力学分析一般借助计算机模拟实现, 可用的模拟软件比较多, 如MS、GRPMACS、LAMMPS等.分子动力学模拟(molecular dynamics simulation, MD simulation)中常用的势函数有Morse势、Tersoff势[56 ] 、Brenner势[57 ] 、REBO势[58 ] 、AIREBO势[59 ] 等.求解牛顿运动方程的数值解法有Verlet算法、Leap-frog算法、Gear校正预测法、Velocity-Verlet算法、Beeman算法等.除了遵从牛顿定律之外, 分子动力学模拟中的粒子还需遵从系综规律.根据改变状态变量, 如粒子数N 、温度T 、压力P 和体积V 等, 系综分为微正则系综、正则系综、等温等压系综和等温等焓系综.由于原子动能与体系温度有关, 因此在恒温条件下进行的分子动力学模拟还需要对体系温度进行控制, 常用的控制温度方法有速度标度法和热浴法等. ...
A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons
1
2002
... 分子动力学方法将N 个粒子组成的物理系统抽象成N 个相互作用的质点, 选定N 个质点间相互作用的势函数后, 在选定的初始条件、边界条件、时间步长下, 通过求解经典牛顿动力学方程求出各个粒子的运动轨迹和速度分布, 最后根据统计理论得出系统热力学和动力学性质.分子动力学分析一般借助计算机模拟实现, 可用的模拟软件比较多, 如MS、GRPMACS、LAMMPS等.分子动力学模拟(molecular dynamics simulation, MD simulation)中常用的势函数有Morse势、Tersoff势[56 ] 、Brenner势[57 ] 、REBO势[58 ] 、AIREBO势[59 ] 等.求解牛顿运动方程的数值解法有Verlet算法、Leap-frog算法、Gear校正预测法、Velocity-Verlet算法、Beeman算法等.除了遵从牛顿定律之外, 分子动力学模拟中的粒子还需遵从系综规律.根据改变状态变量, 如粒子数N 、温度T 、压力P 和体积V 等, 系综分为微正则系综、正则系综、等温等压系综和等温等焓系综.由于原子动能与体系温度有关, 因此在恒温条件下进行的分子动力学模拟还需要对体系温度进行控制, 常用的控制温度方法有速度标度法和热浴法等. ...
A reactive potential for hydrocarbons with intermolecular interactions
1
2000
... 分子动力学方法将N 个粒子组成的物理系统抽象成N 个相互作用的质点, 选定N 个质点间相互作用的势函数后, 在选定的初始条件、边界条件、时间步长下, 通过求解经典牛顿动力学方程求出各个粒子的运动轨迹和速度分布, 最后根据统计理论得出系统热力学和动力学性质.分子动力学分析一般借助计算机模拟实现, 可用的模拟软件比较多, 如MS、GRPMACS、LAMMPS等.分子动力学模拟(molecular dynamics simulation, MD simulation)中常用的势函数有Morse势、Tersoff势[56 ] 、Brenner势[57 ] 、REBO势[58 ] 、AIREBO势[59 ] 等.求解牛顿运动方程的数值解法有Verlet算法、Leap-frog算法、Gear校正预测法、Velocity-Verlet算法、Beeman算法等.除了遵从牛顿定律之外, 分子动力学模拟中的粒子还需遵从系综规律.根据改变状态变量, 如粒子数N 、温度T 、压力P 和体积V 等, 系综分为微正则系综、正则系综、等温等压系综和等温等焓系综.由于原子动能与体系温度有关, 因此在恒温条件下进行的分子动力学模拟还需要对体系温度进行控制, 常用的控制温度方法有速度标度法和热浴法等. ...
Molecular dynamics simulation of resonance properties of strain graphene nanoribbons
1
2011
... 2011年, Chowdhury等[18 ] 利用分子动力学方法和UFF力场[30 ] , 计算了不同约束条件、不同尺寸、不同弯曲模态下的扶手椅型和锯齿型单层石墨烯的谐振频率, 并与连续介质板模型得出的谐振频率进行了比较, 指出后者计算出的谐振频率偏大, 并且相对于单边固支, 双边固支时连续介质模型的谐振频率与分子动力学方法计算出的谐振频率更为接近.同年, 顾芳等[60 ] 利用分子动力学模拟和COMPASS力场分析了石墨烯谐振特性, 研究结果表明石墨烯的动态响应对手性不敏感, 尺寸与应变对石墨烯基频的影响强烈依赖于约束条件, 可以通过改变约束条件和尺寸获得谐振频率高、灵敏度高的谐振式传感器.他们还指出用四边固支型石墨烯检测单轴拉伸应变的灵敏度为7800 Hz/nanostrain, 远大于相同长度碳纳米管应变传感器的灵敏度(887 Hz/ nanostrain)[61 ] . ...
Ultra-high sensitivity of super carbon-nanotube-based mass and strain sensors
1
2008
... 2011年, Chowdhury等[18 ] 利用分子动力学方法和UFF力场[30 ] , 计算了不同约束条件、不同尺寸、不同弯曲模态下的扶手椅型和锯齿型单层石墨烯的谐振频率, 并与连续介质板模型得出的谐振频率进行了比较, 指出后者计算出的谐振频率偏大, 并且相对于单边固支, 双边固支时连续介质模型的谐振频率与分子动力学方法计算出的谐振频率更为接近.同年, 顾芳等[60 ] 利用分子动力学模拟和COMPASS力场分析了石墨烯谐振特性, 研究结果表明石墨烯的动态响应对手性不敏感, 尺寸与应变对石墨烯基频的影响强烈依赖于约束条件, 可以通过改变约束条件和尺寸获得谐振频率高、灵敏度高的谐振式传感器.他们还指出用四边固支型石墨烯检测单轴拉伸应变的灵敏度为7800 Hz/nanostrain, 远大于相同长度碳纳米管应变传感器的灵敏度(887 Hz/ nanostrain)[61 ] . ...
Molecular dynamics modeling and simulation of a graphene-based nanoelectromechanical resonator
3
2013
... 2013年, Kang等[62 ] 利用分子动力学模拟和Brenner势研究了可调谐的谐振式石墨烯传感器, 通过静电激励使施加预应力的石墨烯振动, 如图7 所示.研究结果表明基频与作用在石墨烯边缘的平均张力紧密相关, 并指出谐振式石墨烯传感器适合作为超灵敏度加速度计、热传感器和质量计. ...
... 谐振式石墨烯传感器示意图[62 ] ...
... Schematic of a resonant graphene sensor[62 ] ...
石墨烯纳米带谐振特性的基础研究
1
2013
... 同年, 纪翔等[63 ] 使用AIREBO势、Lennard- Jones势和分子动力学模拟方法研究了有气体阻尼时石墨烯谐振频率与气体压强之间的关系, 指出气体阻尼增大, 谐振频率减小, 但气体阻尼对谐振频率影响很小.Kwon等[64 ] 利用分子动力学模拟分析了双边固支时石墨烯基频随附加质量、外力、硅电极电压的变化情况, 并指出谐振式石墨烯传感器用于质量检测时的灵敏度大约可达10-24 g.2014年, Kwon等[65 ] 又设计出十字型谐振式石墨烯传感器, 如图8 所示, 利用分子动力学模拟分析了十字型石墨烯的谐振特性, 指出可以使用该传感检测外力变化. ...
Molecular dynamics modeling and simulations of graphene-nanoribbon-resonator-based nanobalance as yoctogram resolution detector
1
2013
... 同年, 纪翔等[63 ] 使用AIREBO势、Lennard- Jones势和分子动力学模拟方法研究了有气体阻尼时石墨烯谐振频率与气体压强之间的关系, 指出气体阻尼增大, 谐振频率减小, 但气体阻尼对谐振频率影响很小.Kwon等[64 ] 利用分子动力学模拟分析了双边固支时石墨烯基频随附加质量、外力、硅电极电压的变化情况, 并指出谐振式石墨烯传感器用于质量检测时的灵敏度大约可达10-24 g.2014年, Kwon等[65 ] 又设计出十字型谐振式石墨烯传感器, 如图8 所示, 利用分子动力学模拟分析了十字型石墨烯的谐振特性, 指出可以使用该传感检测外力变化. ...
Molecular dynamics simulation study on cross-type graphene resonator
3
2014
... 同年, 纪翔等[63 ] 使用AIREBO势、Lennard- Jones势和分子动力学模拟方法研究了有气体阻尼时石墨烯谐振频率与气体压强之间的关系, 指出气体阻尼增大, 谐振频率减小, 但气体阻尼对谐振频率影响很小.Kwon等[64 ] 利用分子动力学模拟分析了双边固支时石墨烯基频随附加质量、外力、硅电极电压的变化情况, 并指出谐振式石墨烯传感器用于质量检测时的灵敏度大约可达10-24 g.2014年, Kwon等[65 ] 又设计出十字型谐振式石墨烯传感器, 如图8 所示, 利用分子动力学模拟分析了十字型石墨烯的谐振特性, 指出可以使用该传感检测外力变化. ...
... 单层十字型石墨烯分子动力学模拟图[65 ] ...
... MD simulation diagram of a cross-type SLGS[65 ] ...