The oxide single crystals are primarily grown by the Czochralski method. The growth from seed size to cylindrical diameter is the shouldering stage. As the crystal diameter increases, control of shouldering becomes difficult since the heat dissipation and the crucible wall radiation greatly influence the temperature field of the interface[1⇓-3]. Moreover, because of the spontaneous growth of the crystal diameter during the shouldering stage, problems such as bubbles, inclusions, polycrystalline, and even cracking are common[4⇓⇓⇓-8], which adversely affects the shoulder quality. An inclined shouldering is used to solve this problem, which involves simultaneous axial and radial growth. The variation of latent heat per unit time is reflected in the radial and axial directions when shouldering. The smaller the shoulder angle, the
less influence latent heat of crystallization variation has on radial growth and the more advantageous it is to control the speed of shouldering. Furthermore, the tendency of crystal diameter to increase spontaneously can also be reduced by reducing the shoulder angle[1]. Therefore, the speed of shouldering and the shoulder quality are easily realized and an inclined shoulder is generally used in crystal growth.
Because of the irregular shape, high internal stress[9-10], and easy cracking[11] of the inclined shoulder during crystal processing, the majority of the materials are extracted from the equal-diameter part of the crystal, leaving the shoulder with no practical value. Therefore, the growth of inclined shoulder crystals has the problems of time consumption, material waste, high cost, and thermal field size limitation. The shape of the flat shoulder crystal is regular and can be directly used as the equal-diameter part after simple processing. When compared with an inclined shoulder crystal, a flat shoulder crystal has a significantly higher utilization rate[12], and the time consumed by cone shoulder growth can be saved. Therefore, a flat shoulder crystal can solve the problems of an inclined shoulder crystal.
The variation of latent heat of crystallization is mostly reflected in the radial direction in a flat shouldering stage, which has a high requirement on the interface shape and the radial temperature gradient[13-14]. Moreover, the shoulder of the flat shoulder crystal is very thin, and the spontaneous growth tendency of the shoulder diameter is evident. Therefore, controlling the speed and quality of shouldering is very difficult. Furthermore, the pulling rate of flat shoulder is zero, whereas there is a certain pulling rate before and after shouldering. Therefore, changing the pulling rate without affecting the crystal growth is one of the critical issues. Currently, the research results of the growth of flat shoulder crystals was not optimistic due to issues such as small diameter of single crystals, poor internal quality[15], small thickness[6], and cracking[7,16], and there is a lack of systematic studies on the growth of flat shoulder crystals[17⇓⇓⇓-21].
This work studied the growth of flat shoulder crystals by the Czochralski method. The thermal field and growth process of flat shoulder crystals were investigated using numerical simulation and experiment, beginning with the design of the thermal field, the control of speed and quality of shouldering, and the realization of the change in pulling rate. Take congruent lithium niobate (CLN) crystal as an example, the thermal field and growth process of 3-inch flat shoulder CLN crystal were determined and optimized. A series of flat shoulder CLN crystals were grown and the optical homogeneity of the crystal was tested.
1 Experimental
1.1 Design of thermal field and numerical simulation
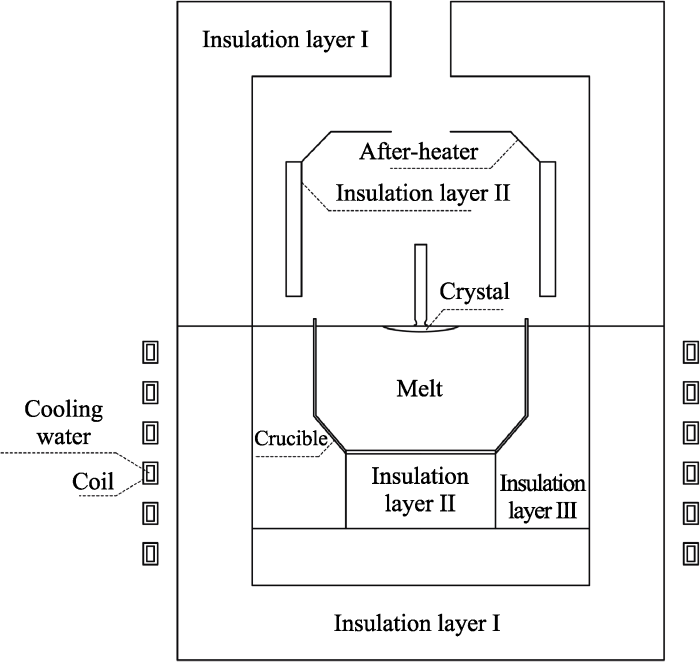
The schematic diagram of thermal field of flat shoulder CLN crystals designed in this work is shown in Fig. 1. The temperature field of crystal growth is obtained by solving the coupled partial differential equation of electromagnetic induction heating, heat conduction, and melt N-S[22]. The calculation results of the last stage are regarded as the initial state, and the temperature field of the next stage is studied iteratively. The isothermal surface of the freezing point of CLN crystal was chosen as the solid-liquid interface at each stage of shouldering. The shape of the solid-liquid interface and the temperature gradient distribution of the interface were simulated.
Fig. 1
1.2 Crystal growth
Materials such as Li2CO3 and Nb2O5 with a purity of 99.99% were weighed and mixed according to a congruent composition molar ratio of Li/Nb = 48.6/51.4, and then sintered at a high temperature to obtain CLN polycrystalline raw material. The amount of raw material in the platinum crucible was estimated by a standard distance of 7-10 mm from the molten surface to the mouth of the crucible. Adjusted the heating power for melting, seeding (seed crystal are c-oriented), necking, and manual shouldering and then transformed into an automatic control and continued to grow.
At the early stage of shouldering, the pulling rate was zero, the weight and the weight change rate of the shoulder were very small. The change in shoulder weight with the diameter and the shape of the crystalline interface may increase, remain unchanged, or even decrease. Therefore, it is impossible to judge the diameter of the shoulder based on the rate of weight change. Moreover, the change in pulling rate before and after shouldering increases the difficulty of calculating the diameter according to the rate of weight change. Moreover, the change in pulling rate before and after shouldering increases the difficulty of calculating the diameter according to the rate of weight change. Therefore, it is necessary to manually observe and judge the change in diameter.
The steps in flat shouldering can be divided into three stages. Firstly, the pulling rate was reduced from 1.5 mm/h to 0 using the set process. The heating power was adjusted slightly to ensure that the thickness of the “neck” remained the same. Secondly, shouldering with zero pulling rate, the heating power was adjusted according to observation and weight change until the crystal diameter slowly increased to approximately 55 mm. Finally, the preset process was used to increase the pulling rate from 0 to 1.5 mm/h, and the heating power was adjusted slightly to ensure the target trend of shouldering. When the pulling rate was increased to 1.5 mm/h, the shouldering was turned into automatic control, and the crystal growth continued.
1.3 Measuring method
The inclusions of the crystal shoulder were judged by the scattered light through the crystal using a He-Ne laser with λ=632.8 nm. The flat shoulder crystal with inclusions was selected and processed into 5 mm×5 mm× 10 mm (x×y×z) crystal blocks. The Z-plane and the detection surface were the surface with inclusions. The morphology of shoulder inclusions was observed by optical microscope and the type of microscope used was OLYMPUS BX51-DIC.
In this work, the optical homogeneity of the crystal was measured by combining the conoscopic interference method[23-24]. The crystal was also processed into 5 mm× 5 mm×10 mm (x×y×z) crystal blocks from the middle part of the crystal shoulder. The optical homogeneity of the crystal was judged according to the shapes of a black cross and concentric rings in the interference pattern.
2 Results and discussion
2.1 Result of crystal growth
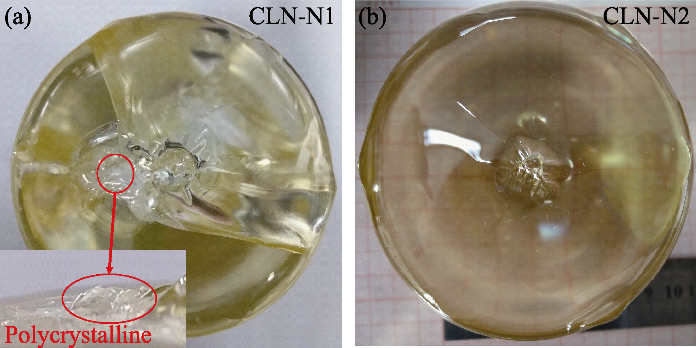
Fig. 2 shows a series of 3-inch flat shoulder CLN crystals grown using different thermal fields and growth processes. Fig. 2(a) shows the flat shoulder CLN crystal grown by thermal field and growth process of the inclined shoulder, representing crystal number: CLN-N1. The crystal cracks from the shoulder to the tail of cylindrical crystal. Fig. 2(b) shows the flat shoulder CLN crystal grown after optimizing the thermal field structure, represented by crystal number: CLN-N2. There is no cracking on the shoulder, but there are inclusions on the shoulder. Fig. 2(c-g) shows the flat shoulder CLN crystal grown after optimizing the speed of shouldering and rotation rate of the crystal based on optimizing the thermal field. The quality of the shoulder is good here. Fig. 2(c-e) show CLN crystals, representing crystal numbers CLN-Y1, CLN-Y2 and CLN-Y3, respectively. Figs. 2(f, g) show the pictures of 0.01%Fe:CLN crystal (Fe:CLN-Y4 ) and 0.01%Er:CLN crystal (Er:CLN-Y5) (in mol), respectively.
Fig. 2
Fig. 2
Photos of series flat shoulder CLN crystals grown by different methods
(a) Non-optimized thermal field and growth process, as CLN-N1; (b) Optimized thermal field, as CLN-N2; (c-g) optimized thermal field and growth process, as CLN-Y1, CLN-Y2, CLN-Y3, Fe:CLN-Y4 and Er:CLN-Y5, respectively
The growth parameters of series flat shoulder CLN crystals are shown in the Table 1.
Table 1 Growth parameters of flat shoulder CLN
| Crystal | CLN-N1 | CLN-N2 | CLN-Y1 | CLN-Y2 | CLN-Y3 | Fe:CLN-Y4 | Er:CLN-Y5 |
|---|---|---|---|---|---|---|---|
| Distance between after-heater and crucible/mm | 20 | 20 | 10 | 10 | 10 | 10 | 10 |
| Time of shouldering/min | - | 200 | 720 | 540 | 320 | 310 | 370 |
| Rotation rate/(r·min-1) | 6 | 6 | 7 | 7 | 7 | 7 | 7 |
| Range of reducing pulling rate/(mm·h-1) | 1.5-0 | 1.5-0 | 1.5-0 | 1.5-0 | 1.5-0 | 1.5-0 | 1.5-0 |
| Decrement of pulling rate each step/(mm·h-1) | 0.5 | 0.3 | 0.3 | 0.2 | 0.2 | 0.2 | 0.2 |
| Interval of reducing pulling rate/min | 20 | 20 | 15 | 10 | 10 | 10 | 10 |
| Range of lifting pulling rate/(mm·h-1) | 0-1.5 | 0-1.5 | 0-1.5 | 0-1.5 | 0-1.5 | 0-1.5 | 0-1.5 |
| Increment of pulling rate each step/(mm·h-1) | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| Interval of lifting pulling rate/min | 20 | 20 | 13 | 15 | 13 | 15 | 10 |
2.2 Design and optimization of thermal field
Discontinuities of the flat shoulder can easily occur when the solid-liquid interface is concave to melt. The flat crystalline interface makes the shoulder just a very thin layer, which is very fast for heat dissipation. The accelerated growth of diameter and the significant driving force of crystal growth lead to the formation of polycrystalline and bubbles. The increase in diameter lead to the failure of shouldering once the inversion of the flat interface occurs[13,25]. Meanwhile, the radial temperature gradient near the interface should not be too small. Otherwise, controlling the speed of shouldering will be difficult, and the quality of crystal will be reduced. Therefore, the convex (to melt) interface and certain radial temperature gradient at the shouldering stage were prerequisites for flat shouldering.
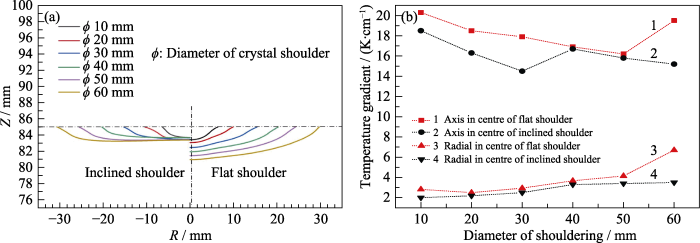
To achieve the convex interface of the shoulder and radial temperature gradient, reasonable design of the thermal field and growth process are very important. The interface shape and temperature gradient at the stage of flat shouldering are simulated by referring to the thermal field of inclined shoulder crystal, as shown in Fig. 3. The result shows that the interface shape of the flat shoulder crystal remains convex to melt, and the curvature of the interface is more significant than that of the inclined shoulder. The flat shoulder is thinner than the inclined shoulder, and the heat dissipation at the solid-liquid interface is easier than that at the inclined shoulder. Therefore, the temperature gradient near the interface is large. The axial temperature gradient at the center of the solid-liquid interface shown in Fig. 3(b) also verifies the results. A more significant axial temperature gradient at the center of the solid-liquid interface may promote the axial crystal growth and make the interface more convex. Meanwhile, the simulation results show that the radial temperature gradient at the edge of the interface increased slightly, which also benefits controlling the speed of shouldering. Therefore, this thermal field was used to grow flat shoulder crystals.
Fig. 3
Fig. 3
Interface shape (a) and temperature gradient (b) of inclined shoulder and flat shoulder
Colorful figures are available on website
The shoulder of the crystal shown in Fig. 4(a) corresponds to the crystal CLN-N1, which was cracked. The reason may be that the driving force of growth was too large during shouldering, which made the spontaneous nucleation of different crystal lattice structure with the seed. Thus, polycrystalline was formed[26-27], as shown in the raised part in Fig. 4(a). The thermal stress of flat shoulder was large because of the large temperature gradient during shouldering[28]. The internal stress of the polycrystalline position was larger because the polycrystalline deteriorates the integrity of the crystal structure[29]. Therefore, during the cooling process[30], the crystal cracks along the polycrystalline with the greatest stress extend to the equal-diameter part of crystal.
Fig. 4
Fig. 4
Flat shoulder morphologies of CLN crystals
(a) Before optimized the thermal field; (b) After optimized the thermal field
The distance between the after-heater and the crucible was reduced by 10 mm to improve the cracks. The simulation results indicated that the temperature gradient near the interface was reduced, while the interface shape and radial temperature gradient change were small after adjusted the thermal field. The crystal was grown using the optimized thermal field, and the shoulder is shown in Fig. 4(b), corresponding to the crystal CLN-N2. The radiation insulation effect of the after-heater on the melt and crystal is strengthened as the distance between the bottom of the after-heater and the melt surface decreases; therefore, the temperature gradient near the interface decreases[31]. Meanwhile, low-temperature gradient avoids the excessive driving force and the formation of polycrystalline, and also reduces the thermal stress during shouldering[32]. Therefore, the problem of cracking caused by excessive stress was solved using an optimized thermal field, and similar methods and mechanisms are also used in silicon single crystals[33-34].
2.3 Control of the speed of shouldering
In the flat shouldering stage, the heat transfer of the crystal shoulder is mostly affected by the diameter, and the accelerated growth trend of the shoulder is complicated[1,35]. Bubbles, polycrystalline and cracking will occur because of the excessive speed of shouldering. Therefore, controlling the speed of shouldering is the key to flat shoulder crystal growth.
Observation provides the speed of shouldering in the early stages of shouldering. The speed of shouldering is judged by observation and simulation of the rate of weight change in the middle and late stages when the crystal weight accumulates to a certain extent and can reflect the change in diameter. The diameter of the crystal is very small at the early stage of shouldering, and the change of heat transfer is limited. The latent heat of crystallization is directly lost from the thin shoulder as the diameter increases. Since the heat dissipation area has a square relationship with crystal diameter, the speed of heat dissipation increases significantly. Therefore, the speed of shouldering was accelerated[36]. The accelerated trend of shouldering will gradually weaken because of the influence of radiation insulation of the crucible wall, with the edge of the shoulder being closer to the crucible wall. Therefore, the control of the speed of shouldering is mainly based on the monitoring. In the early stage of shouldering, the heating power is slightly adjusted to maintain the trend of shouldering. In the middle stage of shouldering, if the crystal has a certain speed of shouldering, there is no need for adjustment. The heating power can be slightly increased when the speed of shouldering is too fast. In the later stage of shouldering, the accelerated trend of shouldering was small, slightly reducing the heating power to keep shouldering.
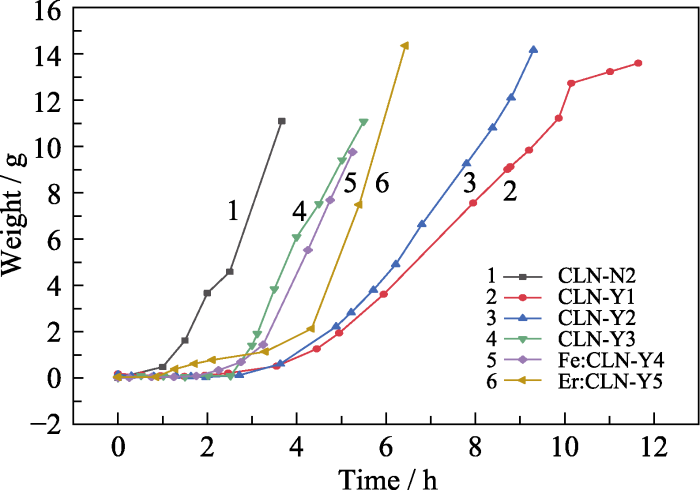
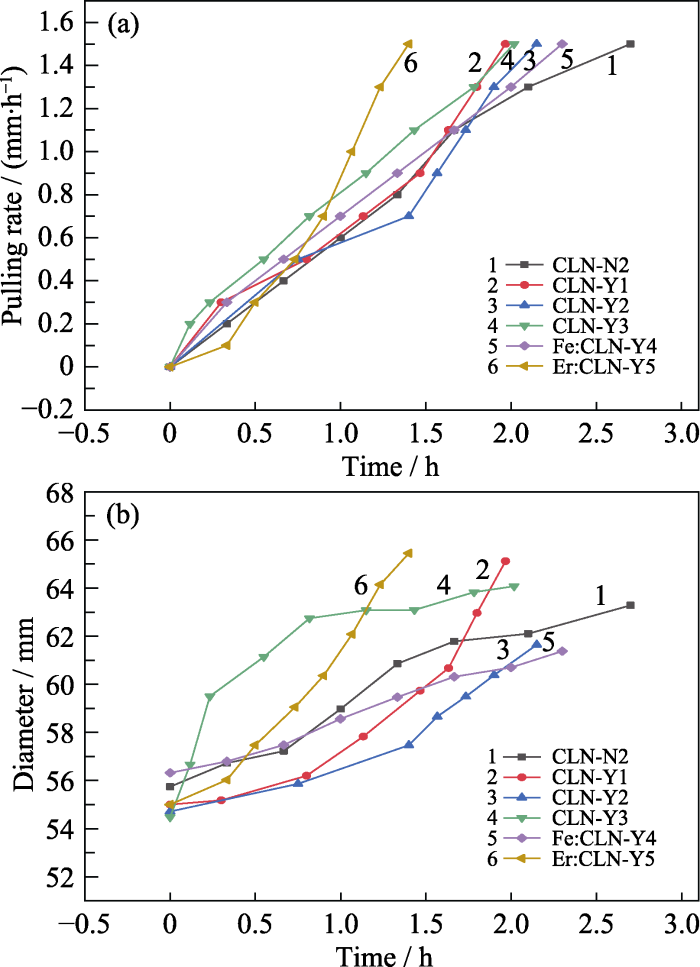
Fig. 5 shows the crystal weight change of shouldering. The result shows that the change of crystal weight is small before the shoulder diameter reaches 30 mm (in the early stage of shouldering), and the speed of shouldering is controllable. When the shoulder diameter of the CLN crystal is 30-35 mm (in the middle and later stage of shouldering), and the doped CLN crystals (Fe:CLN-Y4, Er:CLN-Y5) are 20 mm, the weight and diameter of the crystal begins to increase rapidly. The difference in initial diameter increasing rapidly between the CLN and doped CLN is due to the change in the crystal growth behavior caused by doping.
Fig. 5
Fig. 6(a) shows that the inclusions appeared on the shoulder were bubbles observed using a microscope. The formation of bubbles is because the speed of shouldering is too fast as shown in Fig. 5 (curve 1). The bubbles are discharged from the crystallization interface and accumulate in the solute boundary layer. The bubbles were supersaturated due to insufficient diffusion, and finally, adsorbed on the interface and grew into the crystal[37]. In addition, an unreasonable rotation rate leads to the solute boundary layer becoming thick, and bubbles cannot diffuse out from the boundary layer in time, which will also lead to bubbles growing into crystals[38].
Fig. 6
Fig. 6
Photos of CLN crystal flat shoulder
(a) Before optimized the speed of shouldering; (b-f) After optimized the speed of shouldering
To mitigate the bubble problem, the shouldering speed was reduced as shown by the curve 2 in Fig. 5, and the rotation rate was increased from 6 to 7 r/min. The result of grown crystal in Fig. 6(b) shows inclusion problem was solved. Subsequent crystals (Numbered CLN-Y1 to Er:CLN-Y5) grew at 7 r/min. However, the time of shouldering was increased by 9 h, and the period of growth was significantly increased. Combined with the characteristics of shouldering and the position of inclusion, the method that increases the speed at the beginning and decreases the speed at the middle and later stages of shouldering was adopted. This method can shorten the period of shouldering and keep the shoulder without inclusion. Finally, the process of shouldering was completed in 5-7 h, as shown in the curves 4-6 in Fig. 5, and the quality of shoulder was good, as shown in Fig. 6(d-f).
2.4 Realization of variable pulling rate
2.4.1 Reducing pulling rate
At the stage of decreasing pulling rate, the diameter is as small as a seed crystal, and the target trend is for the diameter to remain unchanged or slightly increase. Therefore, it can be assumed that the required latent heat of crystallization in unit time remains unchanged at this stage. According to energy conservation at the solid-liquid interface[1], the heating power should be reduced appropriately to reduce the pulling rate and ensure the diameter of crystal remains constant or slightly increases.
The time of decreasing pulling rate for the CLN crystal was 1.5 h, referring to the time of increasing diameter from 5 mm (the size of the neck) to approximately 15 mm in the growth of inclined shoulder crystal. The process is reduced by 0.3 mm/h every 20-30 min, taking approximately 100 min to finish. Meanwhile, the power is adjusted slightly to ensure that the diameter increases slightly. It can be proved from Fig. 6(a) that the process is feasible. The interval of adjustment of the pulling rate is shortened to optimize the process and shorten the period. The process was changed to decrease every 10-15 min, taking approximately 60-100 min to finish. The growth process parameters are shown in Table 1. The results of the crystal growth are shown in Fig. 6(b-f), demonstrating the optimized process available. This indicates that the crystal diameter is very small in the stage of reduction of the pulling rate, and the small change in pulling rate has no significant influence on the thermal field. Moreover, adjusting the heating power can compensate for the change in pulling rate.
2.4.2 Lifting pulling rate
The lifting pulling rate is the stage at which the pulling rate increases from zero to equal-diameter pulling rate after flat shouldering. According to the energy conservation at the solid-liquid interface[1], increasing the pulling rate and keep shouldering increases the required latent heat of crystallization in unit time. It is generally achieved by increasing the heat loss from the crystal to the environment or reducing the heat transferred from the melt to the solid-liquid interface. Different from the pulling rate reducing stage, the influence of the crystal diameter on the thermal field cannot be ignored, and the speed of shouldering is still accelerated, or the acceleration is just slowing down. In order to ensure the trend of shouldering and the quality of crystal during the increasing pulling rate, the adjustment strategy is as follows. Do not adjust the heating power or increase it slightly when the shoulder is still accelerated, and reduce the heating power slightly when the speed of shouldering is very slow.
The time of lifting pulling rate refers to the time it takes for the diameter to increase from approximately 55 mm to 65-70 mm in the growth of inclined shoulder crystal, which is approximately 2 h. Therefore, the initial process is lifting 0.2 mm/h every 20-30 min, to approximately 150 min at 1.5 mm/h. When lifting the pulling rate, the heating power was adjusted slightly to keep the suitable increasing trend of diameter. Fig. 7(a) is the change of pulling rate and Fig. 7(b) is the change of diameter during the lifting pulling rate. The inaccuracy is introduced artificially but without influencing the process. The initial process and diameter changes corresponding to curve 1 is shown in Fig. 7. The crystal shoulder is shown in Fig. 6(a), which indicates that the process is feasible.
Fig. 7
In order to optimize the process, the interval was shortened from 20-30 min to 10-20 min, increasing by 0.2 mm/h each time, and it could be increased from 0 to 1.5 mm/h within 1.5-2 h. The growth process parameters are shown in Table 1.The processes are shown in curves 2-6 in Fig. 7. The corresponding grown crystals were CLN-Y1, CLN-Y2, CLN-Y3, Fe:CLN-Y4 and Er:CLN-Y5. The result indicates that the optimized process can increase the pulling rate within 1.5-2 h without affecting the trend of the shouldering and quality of shoulder, and the time taken is shorter than that of the inclined shoulder.
2.5 Results of the crystal test
The optical homogeneity of the flat shoulder crystal without inclusion was tested, and the result shows the optical homogeneity of the crystal can satisfy the requirements. Fig. 8 shows the conoscopic interference pattern of different parts of CLN-Y2 crystal. In the interference pattern, the black cross is orthogonal without distortion, and the concentric rings are symmetric without distortion. It demonstrated that the flat shoulder CLN crystal has good optical homogeneity and can satisfy practical requirements.
Fig. 8
Fig. 8
Conoscopic interference pattern of crystal
(a) Part of shoulder; (b) Part of cylindrical crystal
3 Conclusions
In this work, the thermal field and growth process of flat shoulder crystals grown by Czochralski method were analyzed by numerical simulation and experiment. The influence of the design of thermal field, the control of speed of shouldering, and the technology of varying pulling rate on the growth of shouldering was investigated. The result indicated that the shape of the solid-liquid interface should be convex toward melt at the shouldering stage. In order to avoid polycrystalline and cracking, the temperature gradient near the solid-liquid interface should not be too large. The control of the speed of shouldering is monitored mainly and the heating power was adjusted slightly to ensure the trend of shouldering. The method that increases the speed at the initial stage of shouldering and decreases the speed at the middle and later stages of shouldering can shorten the period of shouldering and avoid the formation of inclusion. Through a strategy of small steps to adjust the pulling rate and heating power, the pulling rate can be changed rapidly without affecting the trend and quality of crystal growth. Using the optimized thermal field and growth process, a series of 3-inch flat shoulder CLN crystals have grown with verified optical homogeneity, which can satisfy the practical requirements.
参考文献
Study on numerical simulation of thermal stress at different stages in Kyropoulos sapphire crystal growth
Experimental analysis and modeling of melt growth processes
Blossom of boule shoulder in growing Nd:YAG crystals
Growth technique of Pb2MoO5 single crystal and analysing the causes of crystal cracks
Growth of high quality lithium niobate crystal
Comparison of thermal stress computations in Czochralski and Kyropoulos growth of sapphire crystals
Thermal and stress distributions in larger sapphire crystals during the cooling process in a Kyropoulos furnace
The simulation of the stress distribution in sapphire crystal growth progress
Theoretical analysis of the cracking of crystal grown by Czochralski method
Application of flat crystal formation in Germanium mono-crystal growing
Effect of internal radiation on the solid-liquid interface shape in low and high thermal gradient Czochralski oxide growth
Effect of the shouldering angle on the shape of the solid-liquid interface and temperature fields in sillenite-type crystals growth
Growth of <104> orientated lithium niobate crystals
Radial temperature distribution in LiNbO3 crystals pulled by the Czochralski technique
The study of ϕ100 mm sulfur doped InP single crystal growth
Study on the progress of seeding and shoulder controlling on HP-LEC InP single crystal growth
A heat shield to control thermal gradients, melt convection, and interface shape during shouldering in Czochralski oxide growth
Growth of flat shoulder germanium single crystal using large size ratio of crystal to crucible
Effect of exposed crucible wall on the Czochralski growth of an LN crystal
The effect of the exposed crucible wall and the influence of the crucible position on the LN crystal growth.
A method to measure electro-optic coefficients of crystals by combining conoscopic interference and near optical axis electro-optic modulation
Improvement of optical homogeneity of LN crystal by heat treating
Inversion of the direction of the solid-liquid interface on the Czochralski growth of GGG crystals
Dislocation formation in heavily as-doped Czochralski grown silicon
The cracking of Czochralski-grown crystals
Growth of LN crystal
Dependence of thermal stress evolution on power allocation during Kyropoulos sapphire cooling process
Creation of defects during the growth of semiconductor single crystals and films
Numerical and experimental studies on crack formation in LiNbO3 single crystal
Simulation on effect of heat shield position on the V/G and point defect and thermal stress of Czochralski silicon
Simulation on effect of heat shield position on the melt and solid liquid interface Cz silicon
On the crystal diameter change during the shouldering process in the Czochralski
Bubbles distribution in sapphire crystal grown by Kyropoulos method
Interactions between bubble and interface during KTa1-xNbxO3 crystal growth
Numerical analysis of effect of thermal stress depending on pulling rate on behavior of intrinsic point defects in large-diameter Si crystal grown by Czochralski method