高级检索
无机材料学报

无机材料学报, 2021, 36(6): 645-651 DOI: 10.15541/jim20200507

研究论文

砷化镓晶体力学特性的各向异性计算

董康佳,1, 姜晨,1, 任绍彬2, 郎小虎2, 高睿1, 叶卉1

1.上海理工大学 机械工程学院, 上海 200093

2.上海微高精密机械工程有限公司, 上海 201203

Anisotropic Calculation of Mechanical Property of GaAs Crystal

DONG Kangjia,1, JIANG Chen,1, REN Shaobin2, LANG Xiaohu2, GAO Rui1, YE Hui1

1. College of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

2. Shanghai Nanpre Mechanics Co. Ltd., Shanghai 201203, China

通讯作者: 姜 晨, 教授. E-mail:jc_bati@163.com

收稿日期: 2020-08-28   修回日期: 2020-10-15   网络出版日期: 2021-06-20

基金资助: 国家自然科学基金(51475310)
上海市青年科技英才扬帆计划项目(18YF1417700)

Corresponding authors: JIANG Chen, professor. E-mail:jc_bati@163.com

Received: 2020-08-28   Revised: 2020-10-15   Online: 2021-06-20

Fund supported: National Natural Science Foundation of China(51475310)
Shanghai Sailing Program(18YF1417700)

摘要

砷化镓因其良好的光电特性被广泛应用于电子与半导体领域, 为推动砷化镓解理加工技术, 对砷化镓材料力学特性的各向异性进行计算并分析。本研究对砷化镓各个晶面之间的夹角、面间距、原子的密度等结构参数进行计算, 基于广义胡克定律结合压痕实验, 分析砷化镓材料表层弹性模量、泊松比、剪切模量、硬度、断裂韧性等力学特性在{100}晶面沿不同晶向力学性能的变化规律。结果表明: 砷化镓不同晶面间结构参数的不同是导致砷化镓力学特性呈现各向异性的主要原因; 砷化镓在{100}晶面上弹性模量、泊松比、剪切模量的各向异性均呈现出周期性变化, 且{100}晶面的剪切模量为恒值59.4 GPa; 砷化镓{100}晶面硬度的各向异性变化幅度较小, 断裂韧性变化幅度较大, 最小值为0.304 MPa·m1/2, 位于<110>晶向, 确定<110>晶向是裂纹最容易扩展的晶向。

关键词： 砷化镓; 力学特性; 各向异性; 压痕实验

Abstract

Gallium arsenide possesses excellent photoelectric property which have been widely used in electron and semiconductor industries. To promote the cleavage manufacturing technology of gallium arsenide, the anisotropy of mechanical property of gallium arsenide is calculated in this work. The structural parameters, such as angle between the crystal planes, the spacing between planes and density of atoms, were calculated. The change rule of elastic modulus, Poisson’s ratio, shear modulus, hardness and fracture toughness of monocrystalline gallium arsenide on crystal {100} plane with crystal orientation was analyzed by generalized Hooke’s law and indentation tests. The results show that difference of structural parameters between planes is the main reason for the anisotropy of mechanical properties of GaAs. With variation of crystal orientation, the elastic modulus and Poisson’s ratio on the {100} crystal plane appear periodic changes, while shear modulus is identically equal to 59.4 GPa. Anisotropy of GaAs {100} crystal plane hardness changes slightly while fracture toughness changes greatly with a minimum value of 0.304 MPa·m1/2 in <110> crystal direction which is sensitive to the crack propagation.

Keywords： gallium arsenide; mechanical property; anisotropy; indentation test

PDF (1569KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

董康佳, 姜晨, 任绍彬, 郎小虎, 高睿, 叶卉. 砷化镓晶体力学特性的各向异性计算. 无机材料学报, 2021, 36(6): 645-651 DOI:10.15541/jim20200507

DONG Kangjia, JIANG Chen, REN Shaobin, LANG Xiaohu, GAO Rui, YE Hui. Anisotropic Calculation of Mechanical Property of GaAs Crystal. Journal of Inorganic Materials, 2021, 36(6): 645-651 DOI:10.15541/jim20200507

随着半导体激光器在精密制造、医学、光通信等领域应用和需求的日益广泛, 对半导体激光器制造工艺技术的研究也备受关注[1,2]。以砷化镓为衬底材料的谐振腔面作为半导体激光器关键组成部分, 对半导体激光器的可靠性及性能有着重要的影响[3]。现有的各类超精密制造技术虽然能够达到较高的制造精度[4,5], 但对于表面质量要求极为苛刻的砷化镓材料谐振腔面, 目前主要还是通过解理加工获得理想的平面基板[6]。砷化镓晶体因其结构特点, 力学特性呈现各向异性, 实现高效且稳定的解理加工存在一定的技术难度, 限制了半导体激光器制造技术的进一步发展。

目前, 国内外针对砷化镓材料力学性能及其结构特点展开了系列研究。Chen等[7]通过不同载荷下的压痕试验, 对砷化镓{100}晶面的<100>晶向和<110>晶向进行测试, 得到{100}晶面两个晶向的硬度、弹性模量、断裂韧性等相关参数; Xu等[8]使用波氏压头进行纳米压痕试验, 对砷化镓{100}晶面同一晶向施加不同载荷, 计算出不同载荷下的弹性模量、维氏硬度、断裂韧性, 得到下压载荷与力学参数的规律, 同时对砷化镓的损伤机理进行了说明; Ponraj等[9]使用不同压头在较高温度下对砷化镓进行压痕实验, 得到单一晶向的弹性模量、硬度、残余应力以及压头下压载荷与下压深度的关系, 同时采用电子显微镜对压痕形貌进行观察; Hjort等[10]通过对立方晶体结构的分析, 绘制出砷化镓的晶体结构, 对{111}晶面的特点进行详细介绍, 同时对弹性模量, 断裂韧性进行相关的计算, 得到单个晶面上弹性模量和断裂韧性沿着不同晶向的变化规律。

为推动砷化镓解理制造技术, 完整揭示砷化镓力学特性的各向异性, 本研究基于砷化镓的结构特点, 分析砷化镓力学特性各向异性产生的原因, 并且结合广义胡克定律和压痕试验, 计算出砷化镓弹性模量、泊松比、剪切模量、断裂韧性等力学特性, 得到砷化镓力学特性在{100}晶面沿不同方向上的变化规律, 为进一步提升砷化镓解理加工工艺技术提供指导依据。

1 砷化镓的结构特点

1.1 砷化镓的晶胞结构

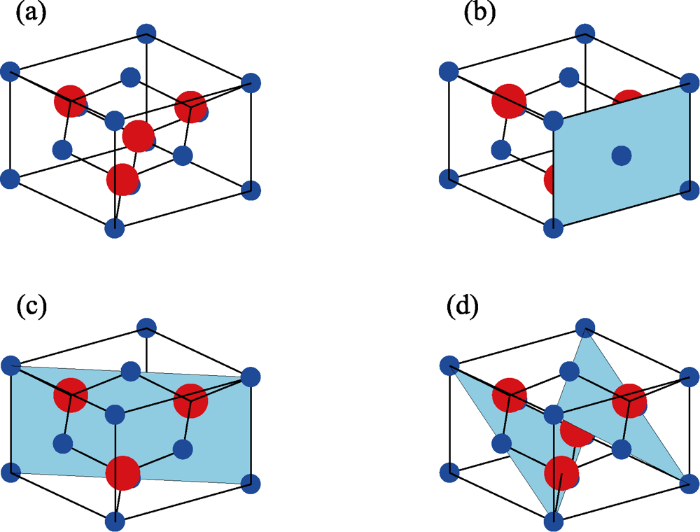
砷化镓(GaAs)作为一种III-V族半导体材料, 属于闪锌矿晶格结构, 单个晶胞结构可以看作是两个面心立方晶格组成, 一个砷晶格和一个镓晶格。若以任一镓原子为空间坐标原点建立坐标系A, a为两相邻顶角原子中心距离, 其四个砷原子的空间坐标分别为(1/4a, 1/4a, 1/4a), (3/4a, 3/4a, 1/4a), (3/4a, 1/4a, 3/4a), (1/4a, 3/4a, 3/4a), 8个镓原子位于在面心立方晶格的8个顶角, 其余6个镓原子位于正六面体的6个面的中心处。砷化镓的各向异性主要表现在如图1所示的三个晶面, 其中镓原子为蓝色, 砷原子为红色。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   砷化镓结构及主要晶面示意图

Fig. 1   Structure and main crystal plane of GaAs

(a) GaAs crystal structure; (b) GaAs (100) plane; (c) GaAs (110) plane; (d) GaAs (111) plane


1.2 砷化镓主要晶面的结构参数

由坐标系A可知, {100}晶面的面间距为a, {110}晶面的面间距为$\sqrt{2}/2a$, {111}晶面的面间距借助于面方程得到。相邻两个{111}晶面的面方程分别为式(1)和式(2):

$ax+ay+az-a=\text{0}$
$ax+ay+az-2a=\text{0}$

进而得到{111}晶面的面间距为$\sqrt{2}/3a$。不同晶面之间的夹角是通过面方程计算出其法向量然后求得夹角。{100}晶面的面方程为式(3)和{110}晶面的面方程为式(4):

ax-a=0
ax-ay=0

{100}晶面、{110}晶面、{111}晶面对应面的空间法向量分别为: (1, 0, 0)、(1, -1, 0)、(1, 1, 1), 由此求出{100}晶面与{110}晶面的夹角为45°, {100}晶面与{111}晶面的夹角为54.74°, {110}晶面与{111}晶面的夹角为90°。

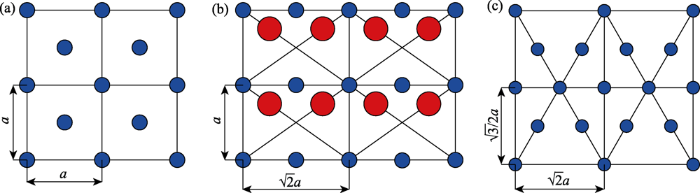
砷化镓主要晶面原子分布如图2所示, 若以单位面积内原子的占有个数来描述其原子分布的密度, 则{110}晶面原子密度>{111}晶面原子密度>{100}晶面原子密度。正是由于各个晶面间的面间距、面夹角、原子密度的不同导致了砷化镓力学特性呈现出各向异性。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   砷化镓各晶面原子分布结构图

Fig. 2   Atomic distribution structure of each crystal plane of GaAs

(a) GaAs (100) plane; (b) GaAs (110) plane; (c) GaAs (111) plane


2 砷化镓的力学性能

2.1 砷化镓的弹性模量

由广义胡克定律可知弹性范围内应力与应变之间呈现线性关系, 可以得出式(5)和式(6)[9], 其中σ为应力, ε为应变, C为刚度矩阵, S为C的可逆矩阵称为柔度矩阵。表达式如下:

$\sigma =C\varepsilon$
$\varepsilon =S\sigma$

因砷化镓为立方晶体结构, 具有高度的对称性, 其中${{S}_{11}}$、${{S}_{12}}$、${{S}_{44}}$为柔度系数。可以将上述式(6)转化为:

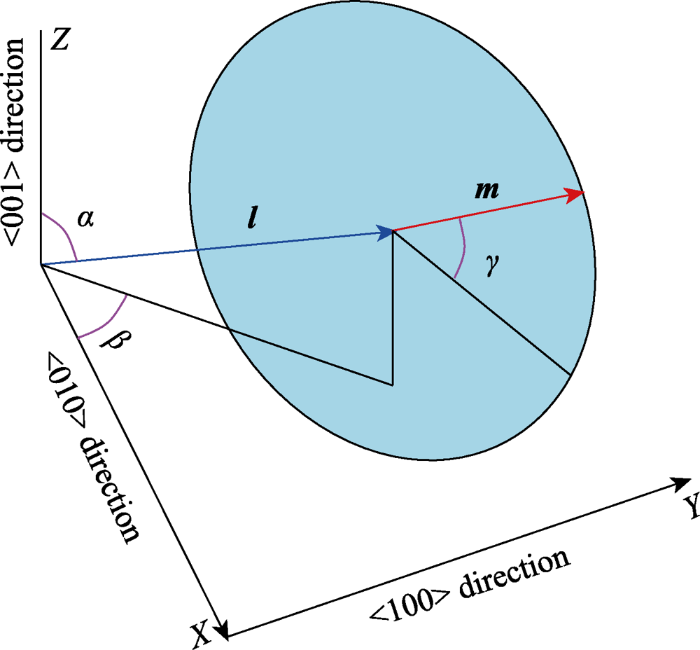
$\left(\begin{array}{l}\varepsilon_{11} \\\varepsilon_{22} \\\varepsilon_{33} \\\varepsilon_{23} \\\varepsilon_{31} \\\varepsilon_{12}\end{array}\right) = \left(\begin{array}{ccccc}S_{11} & S_{12} & S_{12} & & \\S_{12} & S_{11} & S_{12} & & \\S_{12} & S_{12} & S_{11} & & \\& & S_{44} & & \\& & & S_{44} & \\& & & & S_{44}\end{array}\right) \left(\begin{array}{l}\sigma_{11} \\\sigma_{22} \\\sigma_{33} \\\sigma_{23} \\\sigma_{31} \\\sigma_{12}\end{array}\right)$

如图3所示, 在空间中建立直角坐标系B, 三个相互垂直的坐标轴分别为X, Y, Z, 假设l为砷化镓空间晶格内任意方向, ${{l}_{1}}$、${{l}_{2}}$、${{l}_{3}}$分别为<100>晶向、<010>晶向、<001>晶向与l方向上的余弦, 其中α是空间向量l与Z轴所形成的夹角, 而β是l在XY平面的投影与X轴的夹角, m为向量l终点且垂直于l向量的平面(此平面记作剪切面)上的任意向量, γ为向量m与向量l所在延长线在剪切面上投影所形成的夹角。利用柔度矩阵得到砷化镓空间晶格内任意方向上的弹性模量只与向量l有关, 可以表示为式(8)[11,12,13,14,15,16,17]:

$\frac{\text{1}}{E}={{S}_{11}}-2\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right)\left( l_{1}^{2}l_{2}^{2}+l_{1}^{2}l_{3}^{2}+l_{3}^{2}l_{2}^{2} \right)$

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   向量示意图

Fig. 3   Vector diagram


砷化镓{100}晶面上任意方向上的弹性模量可以表示为式(9)[11,12,13,14,15,16,17]:

$\frac{1}{{{E}_{100}}}={{S}_{11}}-2\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right)l_{3}^{2}l_{2}^{2}$

其中:

${{l}_{1}}=\text{sin}\alpha \text{cos}\beta$
${{l}_{2}}=\text{sin}\alpha \text{sin}\beta$
${{l}_{3}}=\text{cos}\alpha$

且$l_{1}^{2}+l_{2}^{2}+l_{3}^{2}=1$,$\ {{l}_{1}}$、${{l}_{2}}$、${{l}_{3}}\in [0,\ 1]$。根据表1中砷化镓的材料参数得到其空间单晶格的弹性模量以及{100}晶面的弹性模量。

表1   砷化镓材料参数[10]

Table 1  GaAs material parameters[10]

Mechanical parameters of GaAsS11/
(×10-12, Pa-1)		S12/
(×10-12, Pa-1)		S44/
(×10-12, Pa-1)
Value11.73.716.8

新窗口打开| 下载CSV


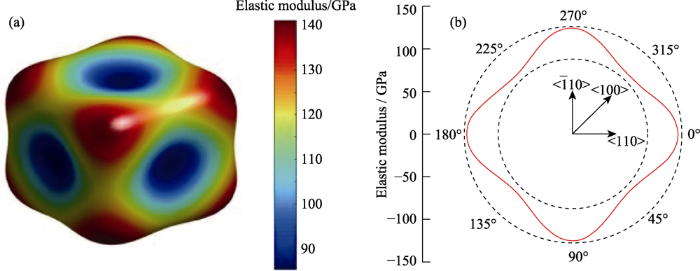
由上述公式可绘制出图4(a)砷化镓空间单晶格的弹性模量以及图4(b)砷化镓{100}晶面沿不同晶向的弹性模量, 进而得到砷化镓空间单晶格弹性模量最大值在<110>晶向处与面心立方晶格的8个顶角所对应, 为141.16 GPa, 最小值位于<100>晶向, 为85.26 GPa。砷化镓{100}晶面的弹性模量呈现周期性变化, 每90°一个周期, 一共4个周期, 若取$<\bar{1}10>$晶向到<110>晶向为一个周期, 其弹性模量的变化是沿着$<\bar{1}10>$晶向到<100>晶向递减, <100>晶向到<110>晶向递增, 且单个周期也存在对称性, 本周期沿着<100>晶向的弹性模量完全对称。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   砷化镓弹性模量

Fig. 4   Elastic modulus of gallium arsenide

(a) Single lattice elastic modulus of GaAs; (b) Elastic modulus of GaAs (100) plane


2.2 砷化镓的泊松比

泊松比是指材料在单向受拉或受压时, 横向正应变与轴向正应变绝对值的比值, 因此砷化镓空间晶格内任意方向l上泊松比不仅与空间上方向l相关, 同时还与垂直于该方向平面上的方向m有关, 设m为该剪切面的任意方向, 如图3所示, ${{m}_{1}}$、${{m}_{2}}$、${{m}_{3}}$为其三个方向的分量, 则砷化镓空间晶格内任意方向l上的泊松比可以表示为式(13)[11,12,13,14,15,16,17]:

$\mu =-\frac{{{S}_{12}}+\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right)\left( l_{1}^{2}m_{1}^{2}+l_{2}^{2}m_{2}^{2}+l_{3}^{2}m_{3}^{2} \right)}{{{S}_{11}}-2\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right)\left( l_{1}^{2}l_{2}^{2}+l_{1}^{2}l_{3}^{2}+l_{3}^{2}l_{2}^{2} \right)}$

砷化镓{100}晶面上任意方向泊松比可以表示为式(14)[11,12,13,14,15,16,17]:

$\frac{1}{{{\mu }_{100}}}=-\frac{{{S}_{12}}-2\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right){{l}_{3}}{{l}_{2}}{{m}_{3}}{{m}_{2}}}{{{S}_{11}}-2\left( {{S}_{11}}-{{S}_{12}}-\frac{{{S}_{44}}}{2} \right)l_{3}^{2}m_{3}^{2}}$

其中:

${{m}_{1}}=\cos \alpha \cos \beta \cos \gamma -\sin \beta \sin \gamma$
${{m}_{2}}=\cos \alpha \sin \beta \cos \gamma +\cos \beta \sin \gamma$
${{m}_{3}}=-\sin \beta \cos \gamma$

并且式(15)、式(16)、式(17)满足此式:$m_{1}^{2}+m_{2}^{2}+m_{3}^{2}=1$,${{m}_{1}}$、${{m}_{2}}$、${{m}_{3}}\in [0,\ 1]$。

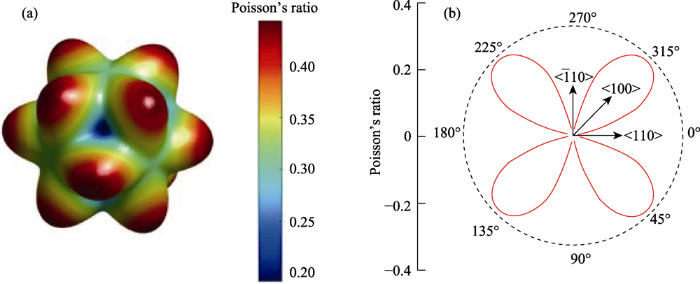
由上述公式可绘制出图5(a)砷化镓空间单晶格的泊松比以及图5(b)砷化镓{100}晶面沿不同晶向的泊松比, 进而得到砷化镓空间单晶格泊松比最大值在<100>晶向处, 值为0.44, 最小值位于<110>晶向, 值为0.19。由图5(b)可知砷化镓{100}晶面的泊松比沿着不同晶向的值呈现出周期性变化, 共存在4个周期, 若取图中0°~270°为一个周期, 即沿着<110>晶向到$<\bar{1}10>$晶向的变化。单个周期内泊松比沿着<110>晶向到<100>晶向递增, 在<100>晶向上出现最大值, 然后沿着<100>晶向到$<\bar{1}10>$晶向递减, 在$<\bar{1}10>$晶向出现最小值, 且单个周期内沿着<100>晶向呈对称性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   砷化镓泊松比

Fig. 5   Poisson’s ratio of gallium arsenide

(a) Lattice Poisson’s ratio of GaAs; (b) Poisson’s ratio of GaAs (100) plane


2.3 砷化镓的剪切模量

砷化镓空间晶格内任一方向上剪切模量与泊松比类似, 与图3中所示l方向和m方向相关, 砷化镓空间晶格内任意方向上的泊松比可以表示为式(18)[11,12,13,14,15,16,17]:

$\begin{align} & \frac{1}{G}=4{{S}_{11}}\left( l_{1}^{2}m_{1}^{2}+l_{2}^{2}m_{2}^{2}+l_{3}^{2}m_{3}^{2} \right)+ \\ & \ \ \ \ 8{{S}_{12}}\left( {{l}_{1}}{{l}_{2}}{{m}_{1}}{{m}_{2}}+{{l}_{1}}{{l}_{3}}{{m}_{1}}{{m}_{3}}+{{l}_{3}}{{l}_{2}}{{m}_{3}}{{m}_{2}} \right)+ \\ & \ \ \ \ {{S}_{44}}\left[ {{\left( {{l}_{1}}{{m}_{2}}+{{l}_{2}}{{m}_{1}} \right)}^{2}}+{{\left( {{l}_{1}}{{m}_{3}}+{{l}_{3}}{{m}_{1}} \right)}^{2}}+{{\left( {{l}_{2}}{{m}_{3}}+{{l}_{3}}{{m}_{2}} \right)}^{2}} \right] \\ \end{align}$

砷化镓{100}晶面上任意方向剪切模量可以表示为式(19)[11,12,13,14,15,16,17]:

$\frac{1}{{{G}_{100}}}=\frac{1}{{{S}_{44}}}$

由上述公式可绘制出图6(a)砷化镓空间单晶格的剪切模量以及图6(b)砷化镓{100}晶面沿不同晶向的剪切模量, 进而得到砷化镓单晶格剪切模量的最大值在{100}晶面, 为59.4 GPa, 最小值位于{110}晶面处, 为32.5 GPa。砷化镓{100}晶面的剪切模量沿着不同晶向的大小相同, 均为59.4 GPa。

图6

新窗口打开| 下载原图ZIP| 生成PPT

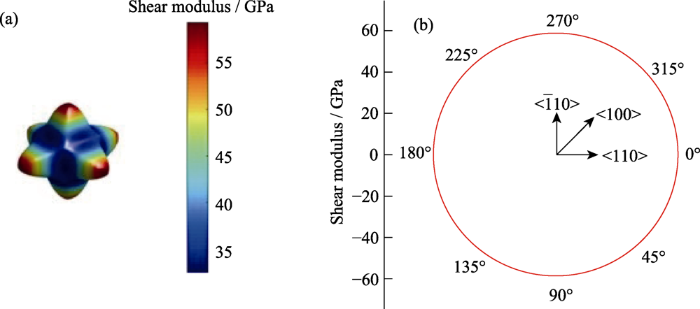
图6   砷化镓剪切模量

Fig. 6   Shear modulus of gallium arsenide

(a) Shear modulus of GaAs spatial lattice; (b) Shear modulus of GaAs (100) plane


3 砷化镓压痕试验

3.1 维氏压痕试验

压痕试验是通过压头垂直压入测试材料, 通过分析压头的下压载荷与在样品上形成的压痕特征, 从而计算得出材料的弹性模量、硬度、断裂韧性等相关力学特性。本次压痕试验, 采用HXS-1000Ak维氏压头显微硬度计, 试验所用压头为标准维氏金刚石压头, 压痕特征的观察也在该设备上进行。进行压痕实验时, 首先对{100}晶面为抛光面的砷化镓晶圆片预处理, 使用金刚石刀将砷化镓晶圆片按标定好的晶向进行切割, 方便压痕试验时确定材料的晶向。其中第一次取向为{100}晶面的<110>晶向, 之后逆时针每间隔15°进行一次取向, 共进行7次取向, 然后使用1.961 N的压力进行加载。

3.2 试验结果分析

砷化镓在相同压力下、不同晶向的压痕形状相同, 但是产生的裂纹长度、压痕的宽度不同, 由此可知不同晶向下的硬度和断裂韧性有差异(图7)。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   砷化镓压痕形貌

Fig. 7   Indentation morphologies of gallium arsenide


根据硬度定义可以求得砷化镓硬度[18,19]:

${{H}_{v}}=1.854\frac{F}{{{(2b)}^{2}}}$

根据压痕断裂力学理论可以求得砷化镓断裂韧性[16,17]:

${{K}_{\text{IC}}}=0.018\sqrt{\frac{E}{{{H}_{v}}}}\frac{F}{{{c}^{3/2}}}$

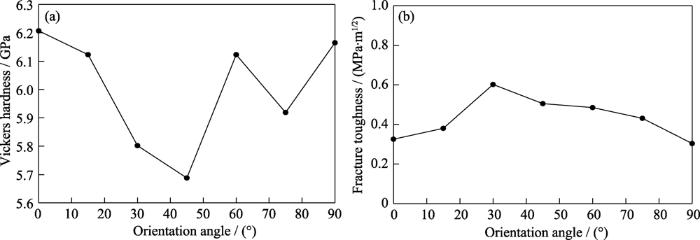
当试验结果满足c/b≥3时, 断裂韧性${{K}_{\text{IC}}}$的值较为准确。其中${{H}_{v}}$为维氏硬度, $F$为施加载荷, b为压痕半对角线长度、c为压痕选取角度对应晶向上的裂纹长度。根据式(20)和式(21)对砷化镓{100}晶面单个周期内的维氏硬度和断裂韧性进行求解。由图8可知: 砷化镓{100}晶面的维氏硬度波动范围较小, 在5.688~6.207 GPa之间, 均值为6.004 GPa, 在<100>晶向上存在最小值5.688 GPa, 在<110>晶向上存在最大值6.207 GPa。砷化镓{100}晶面的断裂韧性波动范围较大, 在0.304~0.602 MPa·m1/2, 均值为0.433 MPa·m1/2, <110>晶向到$<\bar{1}10>$晶向的变化规律为先增大后减小, 在<110>晶向存在最小值0.304 MPa·m1/2, 即{100}晶面上裂纹沿<110>晶向最易扩展。表2为已有相关研究和本次研究结果的汇总比较。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   砷化镓维氏硬度和断裂韧性

Fig. 8   Vickers hardness and fracture toughness of gallium arsenide


表2   断裂韧性和维氏硬度[7,8,9,10]

Table 2  Vickers hardness and fracture toughness[7,8,9,10]

Data sourceHardness/GPaKIC/(MPa·m1/2)Comments
Chen, et al[7]5.27-5.450.482-0.579<110> and <100> crystal direction measured by different loads
Xu, et al[8]6-10-Measured by different loads
Ponraj, et al[9]8.2-10.4-Measured by different loads
Hjort, et al[10]70.44Average value
This work5.69-6.210.30-0.60Measured by single loads and different crystal orientations

新窗口打开| 下载CSV


4 结论

本研究基于砷化镓结构特点, 结合广义胡克定律和压痕试验, 研究了砷化镓的力学特性的各向异性, 结论如下:

1) {100}晶面的面间距为a, <110>晶面的面间距为$\sqrt{2}/2a$, <111>晶面的面间距为$\sqrt{3}/3a$, <110>晶面的原子密度大于{111}晶面的原子密度大于{100}晶面的原子密度; {100}晶面之间的距离大于{110}晶面的距离大于{111}晶面之间的距离; {100}晶面于{110}晶面的夹角为45°, {100}晶面与{111}晶面的夹角为54.74°, {110}晶面与{111}晶面的夹角为90°, 上述参数的不同导致了力学特性的各向异性。

2) 砷化镓空间弹性模量和泊松比以及剪切模量存在高度对称性, 弹性模量最大值为141.16 GPa, 最小值为85.26 GPa, 相差接近39.6%; 剪切模量的最大值为59.4 GPa, 最小值为32.5 GPa, 相差接近45.3%; 泊松比最大值为0.44, 最小值为0.19, 相差接近56.81%, {100}晶面砷化镓弹性模量和泊松比沿着不同晶向呈现4个周期分布, {100}晶面剪切模量沿着不同晶向没有变化, 恒值为59.4 GPa。

3) 砷化镓{100}晶面断裂韧性具有明显各向异性, 最大值与最小值相差49.54%, 在<110>晶向具有最小断裂韧性, 裂纹最容易扩展。

参考文献

WASMER K, BALLIF C, CÉDRIC P, et al.

Dicing of gallium arsenide high performance laser diodes for industrial applications: part I: scratching operation

Journal of Materials Processing Technology, 2008,198(1/2/3):114-121.

DOI      URL     [本文引用: 1]

WASMER K, BALLIF C, POUVREAU C, et al.

Dicing of gallium- arsenide high performance laser diodes for industrial applications: Part II. cleavage operation

Journal of Materials Processing Technology, 2008,198(1/2/3):105-113.

DOI      URL     [本文引用: 1]

WASMER K, BALLIF C, GASSILLOUD R, et al.

Cleavage fracture of brittle semiconductors from the nanometre to the centimetre scale

Advanced Engineering Materials, 2005,7(5):309-317.

DOI      URL     [本文引用: 1]

JIANG C, HUANG J L, JIANG Z Y, et al.

Estimation of energy savings when adopting ultrasonic vibration-assisted magnetic compound fluid polishing

International Journal of Precision Engineering and Manufacturing-Green Technology, 2021,8:1-11.

DOI      URL     [本文引用: 1]

JIANG C, WU T, YE H, et al.

Estimation of energy and time savings in optical glass manufacturing when using ultrasonic vibration- assisted grinding

International Journal of Precision Engineering and Manufacturing-Green Technology, 2019,6(1):1-9.

DOI      URL     [本文引用: 1]

GAO R, JIANG C, LANG X H, et al.

Experimental investigation of influence of scratch features on GaAs cleavage plane during cleavage processing using a scratching capability index

International Journal of Precision Engineering and Manufacturing-Green Technology, 2020, DOI: 10.1007/s40684-020-00241-3.

DOI      [本文引用: 1]

CHEN J Y, DING F, LUO X C, et al.

Fundamental study of ductile- regime diamond turning of single crystal gallium arsenide

Precision Engineering, 2019,62:71-82.

DOI      URL     [本文引用: 4]

XU L X, KONG L Q, ZHAO H W, et al.

Mechanical behavior of undoped n-Type GaAs under the indentation of berkovich and Flat- Tip indenters

Materials, 2019, 12(7): 1192-1-10.

[本文引用: 4]

PONRAJ J S, BUFFAGNI E, DEIVASIGAMANI G, , et al.

Studies of nanoindentation and residual stress analysis of Ge/GaAs epilayers

Semiconductor Science and Technology, 2015, 30(5): 055004- 1-7.

[本文引用: 5]

HJORT K, SODERKVIST J, SCHWEITZ J A.

Gallium arsenide as a mechanical material

Journal of Micromechanics & Microengineering, 1994,4(1):1-13.

[本文引用: 6]

HOPCROFT M A, NIX W D, KENNY T W.

What is the Young's modulus of silicon?

Journal of Microelectromechanical Systems, 2010,19(2):229-238.

DOI      URL     [本文引用: 6]

TING T C T.

On anisotropic elastic materials for which Young’s modulus E(n) is independent of n or the shear modulus G(n, m) is independent of n and m

Journal of Elasticity, 2005,81(3):271-292.

DOI      URL     [本文引用: 6]

KNOWLES K M, HOWIE P R.

The directional dependence of elastic stiffness and compliance shear coefficients and shear moduli in cubic materials

Journal of Elasticity, 2015,120(1):87-108.

DOI      URL     [本文引用: 6]

BRANTLEY W. A.

Calculated elastic constants for stress problems associated with semiconductor devices

Journal of Applied Physics, 1973,44(1):534.

DOI      URL     [本文引用: 6]

LUAN X H, QIN H B, LIU F M, et al.

The mechanical properties and elastic anisotropies of cubic Ni3Al from first principles calculations

Crystals, 2018,8(8):307-309.

DOI      URL     [本文引用: 6]

RYSAEVA L K, BAIMOVA Y A, DMITRIEV S V, et al.

Elastic properties of diamond-like phases based on carbon nanotubes

Diamond and Related Materials, 2019,97:107411.

DOI      URL     [本文引用: 7]

LIU J L, YE L H, ZHOU Y W, et al.

Anisotropy of elasticity of a Ni base single crystal superalloy

Acta Metallurgica Sinica, 2020,56(06):855-862.

[本文引用: 7]

BERGNER F, SCHAPER M, HAMMER R, et al.

Indentation response of single-crystalline GaAs in the nano-, micro-, and macroregime

International Journal of Materials Research (formerly Zeitschrift fuer Metallkunde), 2007,98(8):735-741.

DOI      URL     [本文引用: 1]

CHENG J, NIU Y B, WANG J H, et al.

Analysis of anisotropic mechanical properties of monocrystalline silicon callow

Journal of Harbin Institute of Technology, 2019,51(7):16-23.

[本文引用: 1]

/

〈 〉