大连海事大学 理学院, 大连 116026
中图分类号: TQ174
文献标识码: A
文章编号: 1000-324X(2018)02-0213-06
通讯作者:
收稿日期: 2018-05-8
修回日期: 2018-07-11
网络出版日期: 2019-02-20
版权声明: 2019 无机材料学报编委会 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
基金资助:
作者简介:
作者简介: 于春凤(1995-), 女, 硕士研究生. E-mail: 434319636@qq.com
展开
摘要
三价稀土离子掺杂透明发光材料的f-f跃迁性质可以根据Judd-Ofelt理论进行研究。对于不透明的粉末材料, 由于不能测量其吸收光谱, 难以采用传统的Judd-Ofelt理论进行计算。针对非透明材料, 本研究提出了一种利用漫反射光谱计算稀土掺杂粉末材料Judd-Ofelt参数的方法:首先, 利用Kubelka-Munk方程将漫反射谱转换为强度为相对值的吸收光谱, 然后计算得到相对Judd-Ofelt参数, 再利用荧光衰减测量对相对Judd-Ofelt参数进行修正, 得到真实的Judd-Ofelt参数。将该方法用于计算固相反应合成的Lu2O3:Er3+样品的Judd-Ofelt参数, 并把利用吸收截面计算得到的Er3+的4I13/2能级的辐射跃迁速率与利用Judd-Ofelt参数计算得到的结果进行了比较, 证明研究提出的计算Judd-Ofelt参数的方法是可行的。
关键词:
Abstract
Optical transition properties of trivalent rare earth ions in transparent luminescent materials can be investigated via Judd-Ofelt analysis. The traditional Judd-Ofelt analysis can not be applied to nontransparent powders since its absorption spectra are unable to be measured. Therefore, in this study, a procedure for calculating the Judd-Ofelt parameters was proposed by using defuse-reflection spectrum. Firstly, the defuse-reflection spectrum was transformed into relative absorption spectrum based on Kubelka-Munk function, and then the relative Judd- Ofelt parameters were confirmed from the relative absorption spectrum, at last the actual Judd-Ofelt parameters were obtained by using fluorescence decay data for calibrating the relative values. The method proposed for Judd-Ofelt parameters’ calculation was applied to Lu2O3:Er3+ phosphor prepared by solid-state reaction, and the method was confirmed. The obtained Judd-Ofelt parameters were examined by comparing the radiative transition rates of 4I13/2 derived from the absorption cross section with which obtained from usual route by using the Judd-Ofelt parameters. The present study demonstrated that the proposed Judd-Ofelt analysis route is reliable and practical.
Keywords:
Judd-Ofelt理论是由Judd和Ofelt在上世纪70年代同期独立创立的, 用于描述稀土离子f-f跃迁性质的理论, 其主要理论贡献是对描述稀土离子光学跃迁性质的物理量进行了参数化处理, 并给出理论计算表达式[1,2]。Judd-Ofelt理论一经提出就得到了广泛认可, 并建立起完整可行的稀土离子掺杂材料光学跃迁特性的计算方法[3,4]。虽然Judd-Ofelt理论在计算三价稀土离子光学跃迁特性方面取得了巨大成功, 但也存在一些明显不足。例如, 对于Tm3+及Pr3+掺杂的一些光学材料中获得的三个Judd-Ofelt参数中部分为负值, 其适用性受到了质疑[5,6,7]。因此, 研究者针对一些具体的稀土离子提出了修正的Judd-Ofelt理论, 并在一定程度上解决了这个问题[7,8,9,10]。当测量得到某种三价稀土离子掺杂材料的吸收光谱, 并且已知其掺杂浓度和介质的折射率, 就可以通过标准的Judd-Ofelt计算方法获得相关参数, 从而确定稀土离子在该基质材料中各跃迁的辐射跃迁速率、荧光分支比及辐射跃迁寿命(也就是本征寿命)。利用这些参数值, 结合实验测量荧光衰减曲线就可以获得相关能级的无辐射跃迁及能量传递等特性[11,12]。
Judd-Ofelt理论在描述稀土离子f-f跃迁特性方面无疑是成功的, 但目前它的应用主要局限于透明材料。在已知吸收光谱的条件下, 通过计算得到的吸收跃迁振子强度与理论振子强度进行拟合就能得到Judd-Ofelt参数[12,13,14]。对于稀土离子掺杂的非透明介质, 由于其吸收光谱测量困难, 使该理论的应用受到限制。尽管如此, 研究者们仍然提出了一些稀土离子掺杂的非透明介质材料光学跃迁性能的计算方法, 例如, 利用激发光谱或发射光谱结合荧光衰减测量进行f-f跃迁性能的计算方法[15,16,17]。这些工作将Judd-Ofelt理论的应用范围从透明材料扩展到粉体材料, 并取得了成功, 为稀土离子掺杂粉体材料光学跃迁性能的研究提供了新的思路。对于同一种稀土离子掺杂发光材料而言, 在吸收光谱中观察到的跃迁数一般多于在激发和发射光谱中观测到的跃迁数。此外, 吸收光谱测量得到不同波长处的强度值是绝对值, 而发射和激发光谱测量得到的是相对值, 并且这些值包含了光源的光谱分布及探测器的响应特性, 必须进行必要的强度修正, 而这些因素都可能给计算结果带来一定的误差。因此, 对于稀土离子掺杂的粉体材料, 发展更为普遍适用和可靠的Judd-Ofelt计算方法是非常必要的。
本工作提出一种利用粉体样品漫反射光谱计算Judd-Ofelt参数的方法。首先, 从粉体样品的漫反射光谱出发, 利用Kubelka-Munk理论获得具有相对强度的吸收光谱, 进而获得相对Judd-Ofelt参数。然后, 通过实验测量得到某能级的荧光衰减寿命与计算结果进行比较, 获得绝对值与相对值间的比例, 最终获得真实的Judd-Ofelt参数值。把该方法应用到高温固相法合成的Lu2O3:Er3+荧光粉, 并对结果进行了讨论和评价。
当光入射至粉末样品上时, 一部分光被样品吸收转化为热能或产生其他波长辐射, 另一部分光进入样品内部, 经过多次反射、折射及散射后返回样品表面出射。样品表面出射与入射相同波长的光强度之比定义为反射比$R(v)$, 反射比与波长(或波数)的关系即为漫反射谱, 即$R(v)=\frac{I(v)}{{{I}_{0}}(v)}$。对于粉体样品, 反射比$R(v)$与吸光度${\alpha }'(v)$关系由Kubelka- Munk方程给出[18,19], 如公式(1)所示:
${\alpha }'(v)=C\frac{{{[1-R(v)]}^{2}}}{2R(v)}$ (1)
式中系数$C$与样品的形貌、测量过程中样品的装载量等因素有关, 在确定的实验条件下其为常数, 则上式中${\alpha }'(v)$为强度值相对的吸光度值。
利用式(1)和振子强度的定义, 可以计算得到样品每个吸收峰所对应跃迁的相对振子强度, 即
${{{f}'}_{\exp }}=\frac{m{{c}^{2}}}{\text{ }\!\!\pi\!\!\text{ }{{e}^{2}}}\int{{\alpha }'(\nu )\text{d}\nu }$ (2)
式中m为电子质量, c为光速, e为电子所带的电荷量, p为圆周率。
根据Judd-Ofelt理论, 电子从初态$\left| (S,L)J \right\rangle $到末态$\left| ({S}',{L}'){J}' \right\rangle $吸收跃迁的电偶极跃迁振子强度为
$\begin{align} & f_{\text{th}}^{\text{ED}}=\frac{8{{\text{ }\!\!\pi\!\!\text{ }}^{2}}mcv}{3h(2J+1)}\frac{{{({{n}^{2}}+2)}^{2}}}{9n} \\ & \ \ \ {{\sum\limits_{\lambda =2,4,6}{{{\Omega }_{\lambda }}\left| \left\langle (S,L)J \right|{{U}^{\lambda }}\left| ({S}',{L}'){J}' \right\rangle \right|}}^{2}} \\ \end{align}$ (3)
其中, h为普朗克常量, n为介质的折射率, J和J°分别为初态和末态角动量的量子数, Ωλ(λ=2, 4, 6)为Judd-Ofelt强度参数(简称J-O参数), $\left\langle (S,L)J \right|$ $\left| {{U}^{\lambda }} \right.\left| ({S}',{L}'){J}' \right\rangle $为初态J到末态J°的跃迁约化矩阵元, 一般认为对介质的依赖较小。
将式(2)和(3)联立并通过最小二乘拟合可确定公式(3)中的Judd-Ofelt参数, 但这里所确定的Judd-Ofelt参数并非研究体系的真实值, 而是相对值, 因为拟合中所用的实验振子强度是相对值, 因此将其表示为Ω ¢λ (λ = 2, 4, 6)。还应该指出的是, 磁偶极允许跃迁不能包括在上面最小二乘拟合计算中, 因为无法计算磁偶极跃迁振子强度在当前条件下的相对值。
获得了相对Judd-Ofelt参数Ω ¢λ (λ = 2, 4, 6)后, 可以利用式(4)计算某一能级$J$向其下各能级跃迁的辐射跃迁速率的相对值。
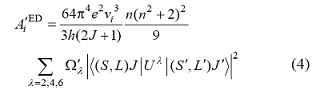
如果以上跃迁中包含磁偶极允许跃迁, 那么磁偶极跃迁速率由式(5)计算,
$A_{i}^{\text{MD}}=\frac{4{{\text{ }\!\!\pi\!\!\text{ }}^{4}}{{e}^{2}}{{n}^{3}}{{v}_{i}}^{3}h}{3(2J+1){{m}^{2}}{{c}^{2}}}{{\left| \left\langle \psi J \right|L+2S\left| {\psi }'{J}' \right\rangle \right|}^{2}}$ (5)
上两式中除$\left| \left\langle \psi J \right|L+2S\left| {\psi }'{J}' \right\rangle \right|$为磁偶极跃迁约化矩阵元外, 其它符号与前面公式中所代表的意义相同。另外, 公式(5)计算得到结果是磁偶极跃迁速率的绝对值。
通过实验测量得到能级$J$的本征寿命, 以便计算该能级的总辐射跃迁速率。为此, 尽量选择能级$J$与下能级间距较大的能级, 以使无辐射跃迁可以忽略; 尽量选择稀土离子掺杂浓度较低的样品, 以使能量传递不存在或可忽略。如果样品的最大声子能量较大, 无辐射跃迁无法忽略, 那么荧光衰减曲线应在低温下测量, 这样可使无辐射速率远远小于辐射跃迁速率; 如果没有浓度较低的样品, 那么测量得到的荧光衰减曲线应采用I-H模型进行分析, 以便得到本征衰减寿命[20]。假设通过实验测量和分析获得的本征寿命为${{\tau }_{\text{r}}}$, 那么由能级$J$到其下面所有能级的总电偶极跃迁速率为
$\begin{matrix} & {{A}^{\text{ED}}}=\frac{1}{{{\tau }_{\text{r}}}}-\sum\limits_{i}{A_{i}^{\text{MD}}}= \\ & \ \ \ \frac{1}{{{\tau }_{\text{r}}}}-\sum\limits_{i}{\left[ \frac{4{{\text{ }\!\!\pi\!\!\text{ }}^{4}}{{e}^{2}}{{n}^{3}}{{v}_{i}}^{3}h}{3(2J+1){{m}^{2}}{{c}^{2}}}{{\left| \left\langle \psi J \right|L+2S\left| {\psi }'{J}' \right\rangle \right|}^{2}} \right]} \\ \end{matrix}$ (6)
式(6)计算出的结果也就是从能级$J$到其下所有跃迁的电偶极跃迁速率的总和, 为真实值。由式(4), 可以计算得到从能级$J$到其下所有跃迁的电偶极跃迁速率总和的相对值${{{A}'}^{ED}}$, 即为
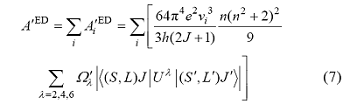
由式(6)和(7)所获得的总的电偶极辐射跃迁速率是不同的, 式(6)给出的是绝对值, 式(7)给出的是相对值, 这是因为式(7)采用的是Judd-Ofelt参数的相对值, 因此${{{A}'}^{\text{ED}}}$与${{A}^{\text{ED}}}$之间的比值就是Judd-Ofelt参数真实值${{\Omega }_{\lambda }}$和相对值${{{\Omega }'}_{\lambda }}$间的比值, 也就是
${{\Omega }_{\lambda }}=\frac{{{A}^{\text{ED}}}}{{{{{A}'}}^{\text{ED}}}}{{{\Omega }'}_{\lambda }}$ (8)
经过以上处理, 就可以利用漫反射谱获得稀土离子掺杂体系的光学跃迁强度参数, 即Judd-Ofelt参数。
样品合成所需原料为光谱纯的Lu2O3、Er2O3和分析纯的NH4HF2, 其中NH4HF2为助熔剂, 既能使反应更加充分, 又可以降低烧结温度并提髙目标产物的结晶性。以上试剂在使用前均未进行任何预处理。
采用传统的高温固相法合成Lu2O3: 1.0mol% Er3+荧光粉, 具体实验过程如下:首先, 按照目标产物的分子式和稀土离子的掺杂浓度, 计算出获得3 g样品所需各反应物的质量; 然后, 用电子秤精确称量出所需各反应物的质量。将称量好的药品倒入玛瑙研钵中, 并加入0.15 g NH4HF2, 研磨30 min使其充分均匀混合。然后, 将均匀研磨后的样品转移到氧化铝坩埚中, 放入马弗炉内, 在1250℃下煅烧2 h, 自然冷却至室温, 将样品取出后研磨并进行收集。
利用日本岛津公司的X射线粉末衍射仪(Shimadzu-XRD-6000)对样品的物相和晶体结构进行分析, 该仪器使用的辐射源为双靶CuKα射线 (λ=0.15405 nm), 阳极的加速电压为40 kV, 工作电流为30 mA, 扫描范围2θ=10°~65°, 扫描步长为0.02°, 扫描速度为2(°)/min。使用Hitachi S-4800型场发射扫描电子显微镜(FE-SEM)对样品的形貌和尺寸进行表征。采用配有积分球的日本岛津公司(Shimadzu)UV-3600紫外可见近红外分光光度计测量样品的漫反射谱, 利用光谱仪生产商提供的BaSO4粉末作为参考试样。采用YAG:Nd3+泵浦的OPO激光器测量荧光衰减, 输出波长调谐在980 nm作为样品激发源, 其脉冲周期为10 ns, 重复频率为10 Hz, 线宽为4~7 cm-1。
图1为Lu2O3: 1.0 mol% Er3+样品的XRD图谱和体心立方相Lu2O3(JCPDS 86-2475)的XRD图谱, 从图可以看出, 样品的衍射峰与标准衍射峰一一对应, 而且在扫描范围内没有出现杂峰, 说明实验制备的样品是纯体心立方相Lu2O3, 同时也表明稀土离子的掺杂并未对样品的晶体结构造成明显影响。
图1 Lu2O3: 1.0mol% Er3+样品和体心立方相Lu2O3(JCPDS 86-2475)的XRD图谱
Fig. 1 XRD patterns of Lu2O3: 1.0mol% Er3+ and Lu2O3 standard card JCPDS 86-2475
图2为Lu2O3:1.0mol% Er3+样品在不同放大倍率下FE-SEM照片, 从照片可以看出, 样品是由许多形状不规则的颗粒组成, 颗粒尺寸不均匀。从高倍率的图片中可以看出, 大的样品颗粒由许多小的颗粒团聚而成, 界限清晰。样品的粒子尺寸多在0.5~2.0 μm范围内。
图2 Lu2O3: 1.0mol% Er3+荧光粉的FE-SEM照片
Fig. 2 FE-SEM images of Lu2O3: 1.0mol% Er3+ phosphor
利用前述漫反射谱计算Judd-Ofelt参数的方法计算固相合成Lu2O3:Er3+荧光粉的光学跃迁强度参数:首先, 将测量得到的漫反射光谱转换成相对强度的吸收光谱; 然后, 计算得到相对Judd-Ofelt参数; 最后, 通过测量4I13/2能级的荧光衰减修正得到Lu2O3中Er3+的光学跃迁强度参数。
3.2.1 相对Judd-Ofelt参数计算
图3(a)给出了Lu2O3:Er3+荧光粉的漫反射光谱图, 图中横轴为波数, 纵轴为反射比。从图中可以观察到11个吸收峰, 分别源于Er3+的基态4I15/2到激发态4I13/2、4I11/2、4I9/2、4F9/2、4S3/2、2H11/2、4F7/2、4F5/2(4F3/2)、2H9/2、4G11/2、4G9/2(2K15/2, 4G7/2)的跃迁, 其中能量由低到高的第8个和第11个吸收峰为两个以上吸收峰重叠而成。利用公式(1)通过数值计算得到相对强度的吸收光谱, 如图3(b), 该图中各吸收峰与图3(a)中各峰一一对应。
图3 Lu2O3:Er3+的漫反射谱(a)和相对吸收光谱(b)
Fig. 3 Defuse-reflection (a) and relative absorption (b) spectra of Lu2O3:Er3+
通过数值计算得到各峰的积分面积, 将能量由低到高算起的第2至第10个吸收峰的面积代入式(2), 计算得到相对实验振子强度, 列于表1的第2列。利用相对实验振子强度并结合式(3), 采用最小二乘法计算得到相对Judd-Ofelt参数, 列于表1的最后一行。将计算得到的相对Judd-Ofelt参数代入到式(3), 计算得到相对理论振子强度, 列于表1的第3列。这里应该说明的是, 图3中第1个跃迁包含了磁偶极成分, 但又不能确定其相对值, 因此不能将其引入计算。此外, 第11个吸收峰由3个激发态吸收叠加, 而且强度又较弱, 为了避免数值计算误差较大, 该峰也未引入计算。
表1 Er3+在Lu2O3中的相对实验振子强度、相对理论振子强度和相对J-O参数
Table 1 Relative experimental oscillator strengths, relative theoretical oscillator strengths for some transitions of Er3+ in Lu2O3 and relative J-O parameters
| Energy level | Relative experimental oscillator strengths, ×10-8 | Relative theoretical oscillator strengths, ×10-8 |
|---|---|---|
| 4I11/2 | 6.16 | 7.01 |
| 4I9/2 | 5.03 | 10.00 |
| 4F9/2 | 23.02 | 51.18 |
| 4S3/2 | 4.61 | 5.43 |
| 2H11/2 | 86.53 | 119.96 |
| 4F7/2 | 8.42 | 31.91 |
| 4F5/2,4F3/2 | 0.96 | 10.27 |
| 2H9/2 | 0.58 | 9.97 |
| 4G11/2 | 53.73 | 210.69 |
| Error: =14.3 Relative J-O parameters: Ω °2=4.43´10-21; Ω °4=3.85´10-21; Ω °6=1.03´10-21 | ||
为了评价拟合结果的质量, 通过下式计算了拟合误差,
$\delta =\sqrt{{{{({{{{f}'}}_{i-\exp }}-f_{i-\text{th}}^{\text{ED}})}^{2}}}/{(N-3)}\;}$ (9)
式中${{{f}'}_{i-\exp }}$和$f_{i-\text{th}}^{\text{ED}}$分别为相对的实验和理论振子强度, $N$为拟合利用的跃迁数, 这里为9, 计算得到的误差(δ =14.3)列在表1的最后一行。比较表1中相对实验和理论振子强度, 对于多数跃迁两者的值都很接近, 计算得到的绝对误差δ 也比较小, 小于多数振子强度值, 这说明最小二乘拟合得到的结果是可靠的。
3.2.2 Judd-Ofelt参数修正
为了利用漫反射谱计算Judd-Ofelt参数的方法获得Lu2O3:Er3+荧光粉的真实Judd-Ofelt参数, 在室温下测量了该材料中Er3+的4I13/2能级荧光衰减曲线, 如图4所示。从图中可以看出, 荧光衰减曲线为一直线, 这说明样品中源于4I13/2能级的能量传递不存在或者可以忽略。同时, 这一结果还说明Er3+被掺杂到Lu2O3中, 样品中不存在大量的Er3+浓度较高的不均匀掺杂区域。此外, Lu2O3基质的最大声子能量(约为600 cm-1)远远小于4I13/2与4I15/2能级间距(约为6500 cm-1), 所以4I13/2能级在室温下的无辐射跃迁可忽略不计[21]。对图4中数据进行线性拟合, 得到斜率的绝对值即为4I13/2能级的辐射跃迁速率, 其倒数就是本征寿命, 拟合结果为${{\tau }_{\text{r}}}$=6.67 ms。
图4 样品4I13/2能级的荧光衰减曲线
Fig. 4 Fluorescent decay curve of 4I13/2 level of Er3+ in Lu2O3 powder
利用式(5)计算得到4I13/2能级的实际磁偶极跃迁速率为${{A}^{\text{MD}}}$=74.83 s-1, 进而获得4I13/2能级的实际电偶极跃迁速率为${{A}^{\text{ED}}}={1}/{{{\tau }_{\text{r}}}}\;-{{A}^{\text{MD}}}$=75.10 s-1。同时, 将相对Judd-Ofelt参数代入到式(7)计算得到4I13/2®4I15/2跃迁的相对电偶极跃迁速率${{{A}'}^{\text{ED}}}$= 25.06 s-1。再利用式(8)计算得到Lu2O3:Er3+的实际Judd-Ofelt参数:Ω2=1.3´10-20 cm2, Ω4=1.16´ 10-20 cm2, Ω6 = 0.31´10-20 cm2。
从式(2)和(3)可以看出, 对于任意一个不包含磁偶极组分的跃迁, Judd-Ofelt参数相对值与真实值间的倍数差异也是真实吸收截面与图3中相对吸收强度间的差异, 因此, 利用${{{A}^{\text{ED}}}}/{{{{{A}'}}^{\text{ED}}}}\;$和图3(b)中的数据可以得到Lu2O3:Er3+吸收截面谱, 结果如图5。利用图5中吸收截面谱的数据, 由式(2)可以计算得到4I15/2®4I13/2跃迁的振子强度
${{f}_{^{4}{{\text{I}}_{15/2}}{{\to }^{4}}{{\text{I}}_{13/2}}}}$=$\frac{m{{c}^{2}}}{\text{ }\!\!\pi\!\!\text{ }{{e}^{2}}}\int_{^{4}{{\text{I}}_{15/2}}{{\to }^{4}}{{\text{I}}_{13/2}}}{\sigma (v)\text{d}v}$ (10)
式中积分限取遍4I15/2®4I13/2跃迁谱带。根据跃迁速率与振子强度的关系, 可以计算得到4I15/2®4I13/2吸收跃迁速率, 即
${{A}_{^{4}{{\text{I}}_{15/2}}{{\to }^{4}}{{\text{I}}_{13/2}}}}=\frac{8\text{ }\!\!\pi\!\!\text{ }{{e}^{2}}{{n}^{2}}{{v}^{2}}}{mc}{{f}_{^{4}{{\text{I}}_{15/2}}{{\to }^{4}}{{\text{I}}_{13/2}}}}$ (11)
由公式(10)和(11), 考虑到Einstein关系就可以得到4I13/2®4I15/2跃迁的辐射跃迁速率, 如下式:
${{A}_{^{4}{{\text{I}}_{13/2}}{{\to }^{4}}{{\text{I}}_{15/2}}}}=\frac{64 \text{ }\!\!\pi\!\!\text{ }{{\nu }^{2}}{{n}^{2}}c}{7}\int{\sigma (\nu ) \text{d}\nu }$ (12)
由上式可知, 无需Judd-Ofelt计算, 而仅从单一4I15/2®4I13/2吸收跃迁截面就可以得到4I13/2®4I15/2跃迁的辐射跃迁速率。利用图5的光谱数据, 由式(12)计算得到${{A}_{^{4}{{\text{I}}_{13/2}}{{\to }^{4}}{{\text{I}}_{15/2}}}}$ = 149.84 s-1。为了验证计算得到的Judd-Ofelt参数的正确性, 将Ωλ代入到式(4), 计算得到4I13/2®4I15/2跃迁的辐射跃迁速率的电偶极部分$A_{^{4}{{\text{I}}_{13/2}}{{\to }^{4}}{{\text{I}}_{15/2}}}^{\text{ED}}$为75.18 s-1, 再利用前面计算得到磁偶极部分$A_{^{4}{{\text{I}}_{13/2}}{{\to }^{4}}{{\text{I}}_{15/2}}}^{\text{MD}}$=${{A}^{\text{MD}}}$=74.83 s-1, 两部分之和为150.01 s-1, 即是总辐射跃迁速率。由上述计算发现, 通过两种途径计算得到的两个辐射跃迁速率非常接近, 说明本研究计算得到的Judd-Ofelt参数是可靠的。
提出了一种用于计算粉末等不透明材料的光学跃迁强度参数(即Judd-Ofelt参数)的方法, 该方法是利用Kubelka-Munk方程将漫反射谱转换为相对吸收光谱, 然后利用相对吸收光谱计算得到Judd-Ofelt参数的相对值, 再通过测量荧光衰减曲线对Judd-Ofelt参数进行修正, 获得真实Judd-Ofelt参数。将该方法应用到固相反应制备的Lu2O3:Er3+样品, 获得了该体系的Judd-Ofelt参数, 并对计算结果进行了验证, 证明研究提出的计算Judd-Ofelt参数的方法是可行的。此外, 研究提出的计算方法还可应用于其它稀土离子掺杂粉末材料的Judd-Ofelt计算。
| [1] |
Optical absorption intensities of rare-earth ions . |
| [2] |
Intensities of crystal spectra of rare-earth ions . |
| [3] |
Judd-Ofelt theory: principles and practices, advances in spectroscopy for laser and sensing . |
| [4] |
50th anniversary of the Judd-Ofelt theory: an experimentalist’s view of the formalism and its application . |
| [5] |
The intensities of lanthanide f ↔ f transitions . |
| [6] |
Spectroscopy of Pr3+ ions in lithium borate and lithium fluoroborate glasses . |
| [7] |
Optical intensities of Pr3+ ions in transparent oxyfluoride glass and glass-ceramic. applications of the standard and modified Judd-Ofelt theories. |
| [8] |
Explicit effects of 4f 5d configuration on 4f 2®4f 2 electric dipole transitions in Pr3+-doped SrAl12O19 . |
| [9] |
Application of standard and modified Judd-Ofelt theories to thulium doped fluoroindate glass . |
| [10] |
Modified Judd-Ofelt technique and application to optical transitions in Pr3+-doped glass . |
| [11] |
Branching ratios, cross sections, and radiative lifetimes of rare earth ions in solids: application to Tm3+ and Ho3+ ions in LiYF4 . |
| [12] |
Optical transition, excitation state absorption, and energy transfer study of Er3+, Nd3+ single-doped, and Er3+/Nd3+ codoped tellurite glasses for mid- infrared laser applications . |
| [13] |
Effect of host glass on the optical absorption properties of Nd3+, Sm3+, and Dy3+ in lead borate glasses . |
| [14] |
Judd-Ofelt analysis of spectroscopic properties of Tm3+, Ho3+ doped GdVO4 crystals . |
| [15] |
Energy levels, fluorescence lifetime and Judd-Ofelt parameters of Eu3+ in Gd2O3 nanocrystals . |
| [16] |
Determination of Judd-Ofelt intensity parameters from the excitation spectra for rare-earth doped luminescent materials . |
| [17] |
Excitation pathway and temperature dependent luminescence in color tunable Ba5Gd8Zn4O21:Eu3+ phosphors . |
| [18] |
Influence of Bi doping on the structure and photoluminescence of ZnO phosphor synthesized by the combustion method . |
| [19] |
Reflectance Spectroscopy: Principles, Methods, Applications, Translated from the German by |
| [20] |
Controllable synthesis and luminescent properties of three-dimensional nanostructured CaWO4:Tb3+ microspheres . |
| [21] |
NIR to visible upconversion in nanocrystalline and bulk Lu2O3:Er3+ . |

/
| 〈 |
|
〉 |