

融合材料领域知识的数据准确性检测方法
收稿日期: 2022-03-21
修回日期: 2022-05-06
网络出版日期: 2022-05-28
基金资助
国家重点研发计划(2021YFB3802101);国家自然科学基金(52073169);之江实验室科研攻关项目(2021PE0AC02)
Detection Method on Data Accuracy Incorporating Materials Domain Knowledge
Received date: 2022-03-21
Revised date: 2022-05-06
Online published: 2022-05-28
Supported by
National Key Research and Development Program of China(2021YFB3802101);National Natural Science Foundation of China(52073169);Key Research Project of Zhejiang Laboratory(2021PE0AC02)
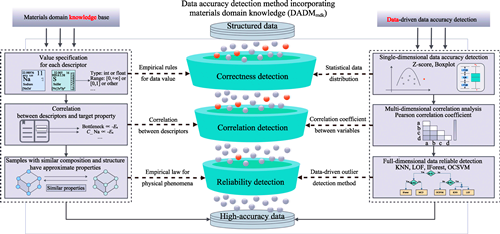
材料数据由于小样本、高维度、噪音大等特性, 用于机器学习建模时常常会产生与领域专家认知不一致的结果。面向机器学习全流程, 开发材料领域知识嵌入的机器学习模型是解决这一问题的有效途径。材料数据的准确性直接影响了数据驱动的材料性能预测的可靠性。本研究针对机器学习应用过程中的数据预处理阶段, 提出了融合材料领域知识的数据准确性检测方法。该方法首先结合材料专家认知构建了材料领域知识库。然后, 将其与数据驱动的数据准确性检测方法结合, 从数据和领域知识两个角度对材料数据集进行基于描述符取值规则的单维度数据正确性检测、基于描述符相关性规则的多维度数据相关性检测以及基于多维相似样本识别策略的全维度数据可靠性检测。对于每一阶段识别出的异常数据, 结合材料领域知识进行修正, 并将领域知识融入到数据准确性检测方法的全过程以确保数据集从初始阶段就具有较高准确性。最后该方法在NASICON型固态电解质激活能预测数据集上的实验结果表明: 本研究提出的方法可以有效识别异常数据并进行合理修正。与原始数据集相比, 基于修正数据集的6种机器学习模型的预测精度都有不同程度的提升。其中, 在最优模型上R2提升了33%。
施思齐 , 孙拾雨 , 马舒畅 , 邹欣欣 , 钱权 , 刘悦 . 融合材料领域知识的数据准确性检测方法[J]. 无机材料学报, 2022 , 37(12) : 1311 -1320 . DOI: 10.15541/jim20220149
Due to the characteristics of small samples, high dimensions, and much noise, materials data often produce inconsistent results with those obtained from domain experts when used for machine learning modeling. For the whole process of machine learning, developing machine learning models embedding materials domain knowledge is a solution to this problem. The accuracy of materials data directly affects the reliability of data-driven materials performance prediction. Here, a data accuracy detection method incorporating materials domain knowledge is proposed by focusing on the data preprocessing stage in the machine learning application process. Firstly, a materials domain knowledge database is constructed based on the knowledge from materials experts. Secondly, it is coordinated with the data-driven data accuracy detection method to perform single-dimensional data accuracy detection based on the rule for value of descriptors, multi-dimensional data correlation detection based on the rule for correlation of descriptors, and full-dimensional data reliable detection based on multi-dimensional similar sample identification strategy from both data and domain knowledge perspectives. For the anomalous data identified at each stage, they are corrected by incorporating the materials domain knowledge. Furthermore, domain knowledge is incorporated into the whole process of the data accuracy detection method to ensure high accuracy of the dataset from the initial stage. Finally, experiments on the NASICON-type solid electrolyte activation energy prediction dataset demonstrate that this method can effectively identify anomalous data and make reasonable corrections. Compared with the original dataset, the prediction accuracy of all six machine learning models based on the revised dataset is improved to different degrees, among which R2 achieves a 33% improvement on the optimal model.

Key words: machine learning; materials science; data quality; domain knowledge
| [1] | MURPHY K P. Machine learning:a probabilistic perspective. Cambridge: MIT Press, 2012. |
| [2] | LIU Y, GUO B R, ZOU X X, et al. Machine learning assisted materials design and discovery for rechargeable batteries. Energy Storage Materials, 2020, 31: 434-450. |
| [3] | LIU Y, ZHAO T L, WU J M, et al. Materials discovery and design using machine learning. Journal of Materiomics, 2017, 3: 159-177. |
| [4] | GUBERNATIS J E, LOOKMAN T. Machine learning in materials design and discovery: examples from the present and suggestions for the future. Physical Review Materials, 2018, 2(12): 120301. |
| [5] | RAMPRASAD R, BATRA R, PILANIA G, et al. Machine learning in materials informatics: recent applications and prospects. npj Computational Materials, 2017, 3: 54. |
| [6] | KATCHO N A, CARRETE J, REYNAUD M, et al. An investigation of the structural properties of Li and Na fast ion conductors using high-throughput bond-valence calculations and machine learning. Journal of Applied Crystallography, 2019, 52: 148-157. |
| [7] | NAKAYAMA M, KANAMORI K, NAKANO K, et al. Data- driven materials exploration for Li-ion conductive ceramics by exhaustive and informatics-aided computations. Chemical Record, 2019, 19: 771-778. |
| [8] | XU Y J, ZONG Y, HIPPALGAONKAR K. Machine learning- assisted cross-domain prediction of ionic conductivity in sodium and lithium-based superionic conductors using facile descriptors. Journal of Physics Communications, 2020, 4: 055015. |
| [9] | CHANDOLA V, BANERJEE A, KUMAR V. Anomaly detection: a survey. ACM Computing Surveys, 2009, 41(3): 15. |
| [10] | BEAL M S, HAYDEN B E, GALL T L, et al. High throughput methodology for synthesis, screening, and optimization of solid- state lithium ion electrolytes. ACS Combinatorial Science, 2011, 13(4): 375-381. |
| [11] | GHARAGHEIZI F, SATTARI M, ILANI-KASHKOULI P, et al. A "non-linear" quantitative structure-property relationship for the prediction of electrical conductivity of ionic liquids. Chemical Engineering Science, 2013, 101: 478-885. |
| [12] | HEMMATI-SARAPARDEH A, TASHAKKORI M, HOSSEINZADEH M, et al. On the evaluation of density of ionic liquid binary mixtures: modeling and data assessment. Journal of Molecular Liquids, 2016, 222: 745-751. |
| [13] | HOSSEINZADEH M, HEMMATI-SARAPARDEH A, AMELI F, et al. A computational intelligence scheme for estimating electrical conductivity of ternary mixtures containing ionic liquids. Journal of Molecular Liquids, 2016, 221: 624-632. |
| [14] | 刘悦, 邹欣欣, 杨正伟, 等. 材料领域知识嵌入的机器学习. 硅酸盐学报, 2022, 50(3): 863-876. |
| [15] | 施思齐, 涂章伟, 邹欣欣, 等. 数据驱动的机器学习在电化学储能材料研究中的应用. 储能科学与技术, 2022, 11(3): 739-759. |
| [16] | OUYANG R, CURTAROLO S, AHMETCIK E, et al. SISSO: a compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Physical Review Materials, 2018, 2: 083802. |
| [17] | CHEN C, YE W K, ZUO Y X, et al. Graph networks as a universal machine learning framework for molecules and crystals. Chemistry of Materials, 2019, 31: 3564-3572. |
| [18] | PARK H, JUNG K, NEZAFATI M, et al. Sodium ion diffusion in NASICON (Na3Zr2Si2PO12) solid electrolytes: effects of excess sodium. ACS Applied Materials & Interfaces, 2016, 8(41): 27814-27824. |
| [19] | LOSILLA E R, ARANDA M A G, BRUQUE S, et al. Sodium mobility in the NASICON series Na1+xZr2-xInx(PO4)3. Chemistry of Materials, 2000, 12(8): 2134-2142. |
| [20] | AGGARWAL C C. Outlier Analysis. 2nd Edition. New York: Springer, 2013. |
| [21] | VANDERVIEREN E, HUBERT M. An adjusted boxplot for skewed distributions. Computational Statistics & Data Analysis, 2004, 52(12): 5186-5201. |
| [22] | SEDGWICK P. Pearson’s correlation coefficient. The British Medical Journal, 2012, 345: e4483. |
| [23] | ZHOU Y, LI S J. BP neural network modeling with sensitivity analysis on monotonicity-based Spearman coefficient. Chemometrics and Intelligent Laboratory Systems, 2020, 200: 103977. |
| [24] | LI R Z, ZHONG W, ZHU L P. Feature screening via distance correlation learning. Journal of the American Statistical Association, 2012, 107(499): 1129-1139. |
| [25] | LIU F T, TING K M, ZHOU Z. Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data, 2012, 6(1): 1-39. |
| [26] | BREUING M M, KRIEGEL H P, NG R T, et al. OPTICS-OF: Identifying density-based local outliers. European Conference on Principles of Data Mining and Knowledge Discovery. Berlin: Springer, 1999. |
| [27] | HARDIN J, ROCKE D M. Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator. Computational Statistics & Data Analysis, 2007, 44(4): 625-638. |
| [28] | HE B, CHI S T, YE A J, et al. High-throughput screening platform for solid electrolytes combining hierarchical ion-transport prediction algorithms. Scientific Data, 2020, 7: 151. |
| [29] | TZORTZIS G, LIKAS A. The MinMax k-means clustering algorithm. Pattern Recognition, 2014, 47(7): 2505-2516. |
/
| 〈 |
|
〉 |