铋层状共生结构铁电体Bi7Ti4NbO21的第一性原理计算

引用本文

刘峰, 陆毅青, 李永祥. 铋层状共生结构铁电体Bi₇Ti₄NbO₂₁的第一性原理计算 . 无机材料学报, 2014, 29(1): 38-42
LIU Feng, LU Yi-Qing, LI Yong-Xiang. First-principles Study of Intergrowth Bismuth Layer-structured Ferroelectric Bi₇Ti₄NbO₂₁ . Journal of Inorganic Materials, 2014, 29(1): 38-42 复制到剪切板

Permissions

This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

铋层状共生结构铁电体Bi₇Ti₄NbO₂₁的第一性原理计算

刘峰^1,², 陆毅青¹, 李永祥¹

1. 中国科学院上海硅酸盐研究所, 无机功能材料与器件重点实验室, 上海 200050

2. 中国科学院大学, 北京 100049

李永祥, 研究员. E-mail:yxli@mail.sic.ac.cn

刘峰(1987-), 男, 博士研究生. E-mail:liufeng@student.sic.ac.cn

基金:上海市优秀学科带头人(10XD1404700)

摘要

铋层状共生结构铁电体Bi₇Ti₄NbO₂₁具有天然的超晶格结构。采用基于密度泛函(DFT)的第一性原理计算对Bi₇Ti₄NbO₂₁及其相关化合物进行了研究。计算得到Bi₇Ti₄NbO₂₁的生成焓为-56.21 eV, 带隙为0.796 eV, 而对于组成单元Bi₃TiNbO₉和Bi₄Ti₃O₁₂, 生成焓分别为-30.72和-43.32 eV, 带隙分别为2.535和2.436 eV。分析表明, 共生结构Bi₇Ti₄NbO₂₁相对于同组分的组成单元处于热力学亚稳态, 其钙钛矿层是电子电导的主要影响因素, 带隙相对于组成单元减小也是源于钙钛矿层的导带底的下移。

关键词: Bi₇Ti₄NbO₂₁; 共生结构铁电体; 第一性原理; 生成焓; 带隙

中图分类号:TQ174 文献标志码:A 文章编号:1000-324X(2014)01-0038-05

First-principles Study of Intergrowth Bismuth Layer-structured Ferroelectric Bi₇Ti₄NbO₂₁

LIU Feng^1,², LU Yi-Qing¹, LI Yong-Xiang¹

1. The Key Laboratory of Inorganic Functional Materials and Devices, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 200050, China

2. University of Chinese Academy of Sciences, Beijing 100049, China

Fund:Program of Shanghai Subject Chief Scientist (10XD1404700)

Abstract

Intergrowth bismuth layer-structured ferroelectric Bi₇Ti₄NbO₂₁ material (iBTN) is a natural super lattice structure with excellent properties. FerroelectriciBTN and parent compounds Bi₃TiNbO₉ (BTN) and Bi₄Ti₃O₁₂ (BiT) were studied with first-principles method based on density functional theory (DFT). The band structures and the density of states of different compounds were calculated based on their optimized structures. The enthalpy of formation and band gaps ofiBTN, BTN and BiT are -56.21, -30.72, -43.32 eV and 0.796, 2.535, 2.436 eV, respectively. The analysis shows that the intergrowth structureiBTN stays at a thermodynamic metastable state in relative to BTN and BiT. The electronic conductivity ofiBTN is mainly depended on the perovskite layers, and the narrowed band gap is attributed to the down shift of the bottom of the conduction band. Detailed partial density of states ofiBTN shows that different perovskite layers have different effects on the conduction band which suggests that the electrons choose their transportation channels in this material. This study can improve the understanding of the intergrowth mechanism and the influence between the structure and the electronic properties ofiBTN.

Keyword: Bi₇Ti₄NbO₂₁; intergrowth bismuth layer-structured ferroelectric; first-principles; enthalpy of formation; band gap

Show Figures

Aurivillius1950年首先发现了铋层状结构铁电材料^{[ 1]}。该类材料的化学通式为(Bi₂O₂)²⁺(A _m_-1B _mO₃ _m₊₁)^2-, m为每两个相邻(Bi₂O₂)²⁺层之间包含的氧八面体的层数。不同层数 m的铋层状化合物可以沿 c轴交替共生, 形成一种超晶格结构, 这种结构称为铋层状共生结构化合物。例如, 由Bi₃TiNbO₉ ( m=2, BTN)和Bi₄Ti₃O₁₂( m=3, BiT), 沿 c轴交替共生形成Bi₇Ti₄NbO₂₁ ( iBTN)。铋层状结构材料不仅具有居里温度高、介电常数低、老化率低、介电击穿强度高、谐振频率的时间和温度稳定性好、机械品质因数较高和易烧结等特点, 在高温和高频领域有广阔的应用前景, 而且在自发极化翻转时不存在疲劳效应, 是用于非易失性铁电存储器 (FeRAM) 的理想材料^{[ 2, 3, 4]}。此外, 铋层状共生结构化合物由于具有丰富的结构和物理性质, 在基础研究领域也备受关注。

本工作利用第一性原理计算的方法研究 iBTN的热力学稳定性和电子结构, 为其共生机制的探讨以及电子结构对电学性质的影响提供理论依据。

1 第一性原理计算

材料研究的传统方法试验周期长, 结果随机性大, 需要投入大量人力物力。近十几年来兴起的第一性原理计算研究不仅避免了上述缺点, 而且可设计性强, 同时可以从理论上对材料的性质做出合理解释, 为人们的研究提供明确指导。

1.1 计算基础

密度泛函理论(DFT)将多体体系的各种物理量与电子密度相关联, 并采用电子密度表示, 因此采用电子密度取代理论计算中的多电子体系波函数^{[ 5">5, 6">6]}, 使实际的理论计算成为可能。第一性原理计算是基于量子力学理论, 除了基本物理参数以外不需要引入经验参数, 通过密度泛函理论来计算预测体系的性质和微观状态的方法。

1.2 计算细节

采用固体物理Castep模块^{[ 7]}, 相关参数设置如下: 采用广义梯度近似(GGA)处理的PBE赝势, 电子能量截断值取为400 eV, 第一布里渊区格点取 6×6×1, 迭代收敛条件分别为能量变化小于2×10^-5eV/atom, 原子力小于0.5 eV/nm, 原子位移变化小于2×10^-4nm, 电子能量收敛阈值小于2×10^-6eV/atom。

2 计算结果和讨论

2.1 结构优化

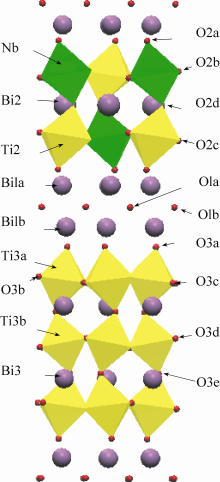
所有相关的结构都采用几何优化得到其稳定结构, 同时计算出它们的总能。表1给出了Bi₄Ti₃O₁₂的优化结果和文献参考值。原始结构所采用的晶胞参数全部来自于文献报告的结果^{[ 8, 9, 10, 11, 12, 13]}。 iBTN 采用正交结构(I 2cm)^{[ 8]}, 如图1所示。Bi₂O₃有四种相结构(α、β、δ和γ), 优化采用最稳定的α相结构^{[ 9]}。类似的, TiO₂有三种晶型(金红石、锐钛矿和板钛矿), 这里采用金红石结构^{[ 12]}。Nb₂O₅采用T-Nb₂O₅结构^{[ 13]}。

	Figure Option View Download New Window
	图1 iBTN的原子位置示意图Fig. 1 The orthorhombic structure of iBTN along [100]

表1 优化得到Bi₄Ti₃O₁₂晶格参数与文献的对比 Table 1 The calculated parameters of Bi₄Ti₃O₁₂ and comparison with published literatures

2.2 生成焓

在合成Bi₇Ti₄NbO₂₁的过程中, 避免Bi₂O₃、TiO₂和Nb₂O₅的形成是非常重要的。为了根据原子化学势确定合适的合成条件, 我们基于不同化合物的总能(每个化学式单元)和组成元素的总能(每个原子)计算了它们的生成焓^{[ 14]}。生成焓的计算依据由方程式(1~6)给出:

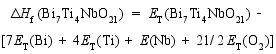(1)

(2)

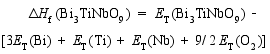(3)

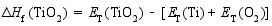(4)

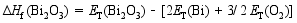(5)

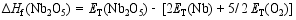(6)

生成焓的计算使用的是在0 K下的总能, 假设随着温度的变化, 其值不会发生大的改变。

由于氧分子的总能不能按照周期性的结构计算得到, 因此我们根据热力学生成焓间接计算氧分子的总能。表2是氧分子总能的结果, 根据不同氧化物计算出值的偏差小于0.1%, BiT、BTN和 iBTN的生成焓所采用的氧分子总能基于三者的平均值。表3列出了 iBTN和其他相关化合物的生成焓数据。共生结构铁电体 iBTN相对于其组成单元BiT或BTN, 生成焓更小, 处在热力学相对稳定的状态, 但和同组成的BiT和BTN相比,处在较高的位置。因此, 共生结构 iBTN在热力学上处在亚稳态, 同组成的BiT和BTN相更为稳定, 这解释了实验上随着温度的升高, 首先生成BiT和BTN, 然后在较高温度下生成共生结构的现象^{[ 19]}。

表2 采用不同氧化物计算得到的氧分子总能 Table 2 Calculated energy of oxygen with different oxides

表3 计算得到的一些化合物的生成焓 Table 3 Calculated energy of oxygen with different oxides

2.3 电子结构

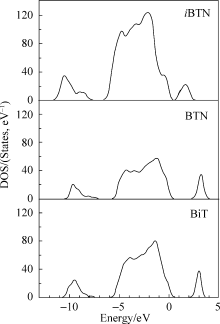
图2显示了结构优化后的 iBTN、BTN和BiT三种结构的态密度。 iBTN的带隙为0.796 eV, 其组成单元BTN和BiT的带隙为2.535和2.436 eV。共生结构铁电体 iBTN的带隙小于其组成单元BiT和BTN, 这主要是由于导带下移所造成的。

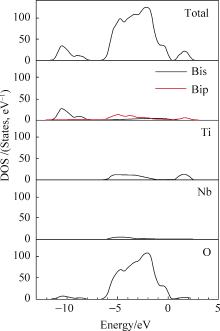
	Figure Option View Download New Window
	图2 iBTN、BTN和BiT的态密度Fig. 2 Total DOS of iBTN, BTN and BiT

图3给出了共生结构铁电体 iBTN的态密度和不同元素的分态密度。价带由O2p、Ti5d、Nb5d、Bi6s和Bi6p态所组成, 其中O的2p态起主导作用; 导带主要是由于Ti和Bi的作用, 其中Ti起大部分作用, 而[TiO₄]是钙钛矿层的主要组成单元, 说明钙钛矿层对导带的影响可能是决定性的。

	Figure Option View Download New Window
	图3 iBTN的态密度和不同元素的分态密度Fig. 3 DOS and partial DOS for different elements of iBTN

为了进一步分析态密度的构成, 对 iBTN中不同的原子作了分态密度图, 如图4所示。

	Figure Option View Download New Window
	图4 iBTN中Bi原子(a), Ti原子和Nb(b), 以及各O原子(c)的分态密度Fig. 4 Partial DOS for Bi (a), Ti and Nb (b) and O (c) of Bi₇Ti₄NbO₂₁

图4(a)是不同Bi原子的分态密度图, 在Bi原子中, 两层钙钛矿层中Bi2原子和三层钙钛矿层中Bi3原子对导带影响占主导, 这再次确定了钙钛矿层是影响导带的主要因素, 而铋氧层中的Bi影响极其有限。在导带的主要贡献者Ti原子中, 三层钙钛矿中间层的Ti原子(Ti3b)的影响最大, 这预示着电子在传输过程中会有优先选择的通道, 如图4(b)。钙钛矿中Bi原子(Bi2和Bi3)导带底相对于铋氧层中Bi限。在导带的主要贡献者Ti原子中, 三层钙钛矿中间层的Ti原子(Ti3b)的影响最大, 这预示着电子在传输过程中会有优先选择的通道, 如图4(b)。钙钛矿中Bi原子(Bi2和Bi3)导带底相对于铋氧气层中Bi原子处于较低的位置, 如图4(a); 钙钛矿层各中心原子(Ti和Nb)也共同参与减小了共生结构的带隙, 见图4(b)。图4(c)给出了氧原子的分态密度图, 二层钙钛矿中O2(a、b、c和d)和三层中O3(a、b、c、d和e)的价带顶比铋氧层中的氧原子O1(1和2)能量位置更低, 事实上, 这和导带底的趋势是一致的, 这再次确定了钙钛矿层同样也是造成共生结构相对于其组成单元带隙减小的影响因素。

3 结论

运用第一性原理计算研究了铋层状共生结构铁电体Bi₇Ti₄NbO₂₁及其相关化合物, 计算得到了它们的生成焓和态密度, 并对热力学稳定性、电子电导和带隙与结构的相互关系进行了阐述, 得到以下结论:

1) 共生结构铁电体 iBTN相对于同组成的BTN和BiT在热力学上处于亚稳状态, 这与文献结果是一致的;

2) 电子结构的计算结果表明, 钙钛矿层是材料电子电导的主要影响因素, 铋氧层几乎没有影响;

3) 共生结构 iBTN的带隙比组成单元都要小, 这个结果虽然有待实验验证, 但深入的计算发现, 钙钛矿层造成了导带底的下移, 从而导致带隙的减小。

The authors have declared that no competing interests exist.

参考文献

View Option

1	Aurivillius B. Mixed bismuth oxides with layer lattices. structure of Bi₄Ti₃O₁₂, Arkiv for Kemi, 1950, 1(6): 499-512. [本文引用:1]
2	Dearaujo C A P, Cuchiaro J D, McMillan L D, et al. Fatigue-free ferroelectric capacitors with platinum-electrodes. Nature, 1995, 374(6523): 627-629. [本文引用:1] [JCR: 36.28]
3	Park B H, Kang B S, Bu S D, et al. Lanthanum-substituted bismuth titanate for use in non-volatile memories. Nature, 1999, 401(6754): 682-684. [本文引用:1] [JCR: 36.28]
4	Yi Z G, Li Y X, Wang Y, et al. Dielectric and ferroelectric properties of intergrowth Bi₇-_xLa_xTi₄NbO₂₁ ceramics. Applied Physics Letters, 2006, 88(15): 152909-1-3. [本文引用:1] [JCR: 3.844]
5	Hohenberg P, Kohn W. Inhomogeneous electron gas. Physical Review B, 1964, 136(3B): B864-B871. [本文引用:1] [JCR: 2.162]
6	Kohn W, Sham L J. Self-consistent equations including exchange and correlation effects. Physical Review, 1965, 140(4A): [本文引用:1]
7	Clark S J, Segall M D, Pickard C J, et al. First principles methods using CASTEP, Zeitschrift Fur Kristallographie, 2005, 220(5/6): 567-570. [本文引用:1]
8	Mercurio D, Trolliard G, Hansen T, et al. Crystal structure of the ferroelectric mixed aurivillius phase Bi₇Ti₄NbO₂₁, International Journal of Inorganic Materials, 2000, 2(5): 397-406. [本文引用:2]
9	Ivanov S A, Tellgren R, Rundlof H, et al. Structural studies of α-Bi₂O₃ by neutron powder diffraction. Powder Diffraction, 2001, 16(4): 227-230. [本文引用:2] [JCR: 0.707]
10	Cucka P, Barrett C S. Crystal structure of Bi and of solid solutions of Pb, Sn, and Te in Bi. Acta Crystallographica, 1962, 15: 865-872. [本文引用:1]
11	Milman V, Winkler B, White J A, et al. Electronic structure, properties, and phase stability of inorganic crystals: a pseudopotential plane-wave study. International Journal of Quantum Chemistry, 2000, 77(5): 895-910. [本文引用:1] [JCR: 1.357]
12	Abrahams S C, Bernstei Jl. Rutile-normal prpperty plot analysis and accurate measurement of crystal structure. Journal of Chemical Physics, 1971, 55(7): 3206-3211. [本文引用:2] [JCR: 3.333]
13	Kato K, Tamura S. Crystal structure of T-Nb₂O₅. Acta Crystallographica Section B-Structural Science, 1975, 31: 673-677. [本文引用:2] [JCR: 2.286]
14	Shah S H, Bristowe P D. Ab initio energetics of lanthanum substitution in ferroelectric bismuth titanate. Journal of Physics- Condensed Matter, 2011, 23(15): 15902-1-12. [本文引用:1]
15	Dorrian J F, Newnham R E, Kay M I, et al. Crystal structure of Bi₄Ti₃O₁₂. Ferroelectrics, 1971, 3(1): 17-27. [本文引用:1] [JCR: 0.391]
16	Lide D R. CRC Hand book of Chemistry and Physics, 90th Edition. Boca Raton: CRC Press, 2010: 791-804. [本文引用:1]
17	Alahmed Z, Fu H. First-principles determination of chemical potentials and vacancy formation energies in PbTiO₃ and BaTiO₃. Physical Review B, 2007, 76(22): 224101-1-8. [本文引用:1]
18	Carlsson J M, Hellsing B, Domingos H S, et al. Theoretical investigation of the pure and Zn-doped alpha and delta phases of Bi₂O₃. Physical Review B, 2002, 65(20): . 205122-1-10. [本文引用:1]
19	高翔. 共生铋层状结构铁电体Bi_{7Ti₄NbO₂₁的微结构研究}. 上海: 中国科学院上海硅酸盐研究所博士论文, 2011. [本文引用:1]

1950

0.0

Arkiv for Kemi. 1950, 1(6):499-512

Mixed bismuth oxides with layer lattices. structure of Bi₄Ti₃O₁₂

Aurivillius B

Several compounds withm= 2, 3, 4, and 5 in the general formula (Me₂′O₂)²⁺ (Me_m–1 R_mO_3m+1)^2– were synthesized, a number of them for the first time. They possess a layer-type crystal structure. Bi³⁺ may be the only suitable ion for the Me′ sites; R may be Ga^s+, Ti⁴⁺, Nb⁵⁺, or Ta⁵⁺. The restrictions on the size of Me ions increases with increasing value ofm. Lattice parameter data for the compounds and indexed X-ray powder patterns form= 5 compounds are presented.

... Aurivillius1950年首先发现了铋层状结构铁电材料^[1] ...

1995

36.28

0.0

... 铋层状结构材料不仅具有居里温度高、介电常数低、老化率低、介电击穿强度高、谐振频率的时间和温度稳定性好、机械品质因数较高和易烧结等特点, 在高温和高频领域有广阔的应用前景, 而且在自发极化翻转时不存在疲劳效应, 是用于非易失性铁电存储器 (FeRAM) 的理想材料^[2,3,4] ...

1999

36.28

0.0

2006

3.844

0.0

1964

2.162

0.0

Theoretical Chemistry Accounts. 2000, 103(3-4):259 - 262 DOI:10.1007/s002149900030

Perspective on “Inhomogeneous electron gas”
Hohenberg P, Kohn W (1964) Phys Rev 136: B864

Matthias Ernzerhof(1) Gustavo E. Scuseria(1)

1.Department of Chemistry, Rice University, P.O. Box 1892, Houston, TX 77005, USA US US

The Hohenberg–Kohn theorems in “Inhomogeneous electron gas” established a whole new perspective for the study of electronic structure theory and marked the birth of modern density functional theory (DFT). In our view, DFT and wavefunction theories complement each other. Starting with the invention of the Kohn–Sham method a fruitful synthesis of DFT and wavefunction theories took place and the most powerful computational tools currently available are combinations of both methods. The Hohenberg–Kohn theorems inspire the quest for simple density functionals of increased accuracy. We believe that the synthesis of accurate density functionals and computationally efficient wavefunction methods will continue to dominate electronic structure theory.

... 1 计算基础密度泛函理论(DFT)将多体体系的各种物理量与电子密度相关联, 并采用电子密度表示, 因此采用电子密度取代理论计算中的多电子体系波函数^[5,6], 使实际的理论计算成为可能 ...

1965

0.0

2005

0.0

... 2 计算细节采用固体物理Castep模块^[7], 相关参数设置如下: 采用广义梯度近似(GGA)处理的PBE赝势, 电子能量截断值取为400 eV, 第一布里渊区格点取 6×6×1, 迭代收敛条件分别为能量变化小于2×10^-5eV/atom, 原子力小于0 ...

2000

0.0

International Journal of Inorganic Materials. 2000, 2(5):397-406

Crystal structure of the ferroelectric mixed aurivillius phase Bi₇Ti₄NbO₂₁

Mercurio D , Trolliard G , Hansen T

The crystal structure of Bi₇Ti₄NbO₂₁ has been solved by X-ray and neutron diffraction data analysis on single crystals. Bi₇Ti₄NbO₂₁ crystallizes with orthorhombic symmetry, I2cm space group witha=5.4420(10) Å,b=5.4040(10) Å,c=57.990(12) Å andZ=2. The structure can be regarded as a mixed Aurivillius phase resulting of a regular intergrowth along thec-axis of one half the unit cell of Bi₄Ti₃O₁₂ and one half the unit cell of Bi₃TiNbO₉ parent Aurivillius phases by sharing ‘Bi₂O₂’ common sheets. Perovskite-like slabs with BiTiNbO₇ and Bi₂Ti₃O₁₀ compositions are distorted in a way close to that observed in Bi₃TiNbO₉ and Bi₄Ti₃O₁₂ ones respectively.

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

... iBTN 采用正交结构(I2cm)^[8], 如图1所示 ...

2001

0.707

0.0

Powder Diffraction. 2001, 16(4):227-230

Structural studies of α-Bi₂O₃ by neutron powder diffraction

Ivanov S A , Tellgren R , Rundlof H

A detailed neutron powder diffraction study of the atomic structure of α-Bi₂O₃ at high temperatures using the Rietveld method was performed to clarify the nature of the unusual magnetic behavior and the origin of the high temperature dielectric anomalies of α-Bi₂O₃ in the temperature interval 300–700 K. Analysis of obtained experimental data shows that there are no evidence of a structural phase transition in α-Bi₂O₃ between 295 and 660 K. The observed high temperature dielectric anomalies in α-Bi₂O₃ are evidently governed by changes in the electron subsystem of the bismuth oxide.

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

... Bi₂O₃有四种相结构(α、β、δ和γ), 优化采用最稳定的α相结构^[9] ...

1962

0.0

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

2000

1.357

0.0

International Journal of Quantum Chemistry. 2000, 77(5):895-910

Electronic structure, properties, and phase stability of inorganic crystals: a pseudopotential plane-wave study

Milman V , Winkler B , White J A

Recent developments in density functional theory (DFT) methods applicable to studies of large periodic systems are outlined. During the past three decades, DFT has become an essential part of computational materials science, addressing problems in materials design and processing. The theory allows us to interpret experimental data and to generate property data (such as binding energies of molecules on surfaces) for known materials, and also serves as an aid in the search for and design of novel materials and processes. A number of algorithmic implementations are currently being used, including ultrasoft pseudopotentials, efficient iterative schemes for solving the one-electron DFT equations, and computationally efficient codes for massively parallel computers. The first part of this article provides an overview of plane-wave pseudopotential DFT methods. Their capabilities are subsequently illustrated by examples including the prediction of crystal structures, the study of the compressibility of minerals, and applications to pressure-induced phase transitions. Future theoretical and computational developments are expected to lead to improved accuracy and to treatment of larger systems with a higher computational efficiency. © 2000 John Wiley & Sons, Inc. Int J Quant Chem 77: 895–910, 2000

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

1971

3.333

0.0

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

... 类似的, TiO₂有三种晶型(金红石、锐钛矿和板钛矿), 这里采用金红石结构^[12] ...

1975

2.286

0.0

... 原始结构所采用的晶胞参数全部来自于文献报告的结果^{[8,9,10,11,12,13]} ...

... Nb₂O₅采用T-Nb₂O₅结构^[13] ...

2011

0.0

... 为了根据原子化学势确定合适的合成条件, 我们基于不同化合物的总能(每个化学式单元)和组成元素的总能(每个原子)计算了它们的生成焓^[14] ...

1971

0.391

0.0

2010

0.0

2007

0.0

2002

0.0

2011

0.0