作者简介: 罗学维(1987-), 男, 硕士研究生. E-mail:610334007@qq.com
以高铝矾土、硅灰为原料, 玉米淀粉为造孔剂制备高气孔率莫来石, 通过XRD、SEM等对产物物相、形貌进行表征, 研究淀粉含量对显气孔率、体积密度和抗折强度的影响, 及不同显气孔率的莫来石随温度变化的导热系数, 建立体积密度、抗折强度与气孔率关系模型及非线性导热模型。结果表明: 体积密度、抗折强度随气孔率增加而减小, 并符合指数函数关系。导热系数随温度的升高而增大, 实测值与非线性导热模型计算值吻合较好, 非线性导热模型能够准确地反映高气孔率莫来石导热系数与温度、气孔率、平均孔径和热辐射等之间的关系。
Highly porous mullite ceramics were prepared by bauxite and silica fume as raw materials and corn starch as the pore-forming agent. The phase and morphology were characterized by XRD and SEM, respectively. The influence of corn starch content on apparent porosity, bulk density and flexural strength were studied. Thermal conductivity of porous mullite was measured at 473-1273 K. A new nonlinear thermal conductivity model and several models between bulk density, flexural strength and apparent porosity were established. The results indicate that, bulk density and flexural strength of porous mullite decrease with porosity increase and conform to the exponential function relationship. Thermal conductivity of porous mullite increases with the rise of temperature and the measured values are in good agreement with values calculated by nonlinear thermal conductivity model. The new model can accurately reflect the thermal conductivity correlations for temperature, porosity, radiation and mean pore size.
多孔陶瓷广泛应用于电池电极、催化剂载体、热气/熔融金属过滤、离子交换吸附、热交换、传感器等领域[ 1, 2, 3, 4, 5]。莫来石(3Al2O3·2SiO2)是常压下热力学稳定的铝硅酸盐, 因其高温下具有低热膨胀系数、良好的抗热震性和抗蠕变性能、优异的机械性能和化学稳定性, 近年, 多孔莫来石的制备、性能及应用研究受到人们广泛关注[ 6]。制备多孔莫来石陶瓷方法主要有添加造孔剂法[ 7]、溶胶-凝胶法[ 8]、发泡法[ 9]、模板法[ 10]、微波烧结法[ 11]等。其中添加造孔剂法为近年制备多孔陶瓷比较常用的方法, 在原料粉体中加入一定量的成孔剂, 如木屑、淀粉、石墨或其他有机微粒[ 6], 工艺简单、成本低廉。Bai 等[ 12]以石墨为造孔剂, 于1500℃煅烧制备得到开口气孔率36.4%的多孔莫来石, 其抗折强度达42.1 MPa。Okada等[ 13]采用粘胶纤维作造孔剂, 利用挤压成型制备多孔莫来石陶瓷。Popa等[ 14]采用相似方法, 改变粘胶纤维的直径范围制备出不同孔径分布的多孔莫来石, 并研究了毛细现象。然而, 这些研究更多注重造孔剂种类、数量与多孔莫来石孔结构、力学性能及催化性能的研究, 较少关注其高温隔热/绝热性能, 尤其其高温导热模型的研究。
多孔材料被认为是由致密固体骨架与空气组成的一个两相系统[ 15], 研究人员提出Series Model (SM)、Maxwell-Eucken1 (ME1)、Parallel Model (PM)、Maxwell-Eucken2 (ME2)和Effective Media Theory Model (EMT)五种经典导热模型[ 16, 17, 18, 19, 20]。Litovsky等[ 21]认为建立材料导热模型要充分考虑材料的结构。烧结莫来石(气孔率≤15%的导热系数随温度的升高而升高; 对大多低气孔率(<20%)材料来说, 导热系数能较好符合ME2模型, 孤立孔隙分散在连续相中; 对于高孔隙率(>60%)材料来说, 孔径尺寸及开、闭孔类型, 导热系数符合几何晶格Frey-Dulne模型, 其固相导热系数可据Lichtenecker model计算。Carson等[ 22]研究了各向同性多孔材料的导热模型认为, 各向同性材料可分闭孔和开孔两类。闭孔材料的最佳传热途径是连续相, 闭孔区域由Hashin-Shtrikman模型解释; 开孔材料最佳传热途径是分散相, 开孔区域由EMT模型解释。Barea等[ 23]采用激光闪射法测量了淀粉原位固化法制备的气孔孔径为~30 μm、气孔率为35~60%多孔莫来石的导热系数。认为多孔莫来石可看成双相材料, 在考虑气孔率、温度、孔径尺寸及辐射传热的情况下, 提出了导热系数与温度相关联的方程, 给出了3个与孔径相关的参数。Wang等[ 19, 20]给出了非均质多孔材料的导热模型, 将Series、Maxwell-Eucken1、Maxwell-Eucken2、Parallel和EMT 五种基本模型统一起来, 建立起基于孔结构参数的统一数学表达式, 这种组合模型比半经验模型更具优势, 但该模型仅由数学推理而得, 并无明确物理基础。Petrasch等[ 24]利用CT三维成像技术对孔结构参数进行表征, 研究多孔材料导热系数与孔结构、温度之间的关系,认为网状多孔陶瓷导热系数与Maxwell’s upper bound和Loeb’s models吻合较好。Shimizu等[ 25]研究了高孔隙率刚玉耐火材料的导热模型, 认为温度高于783 K时, 随温度的升高, 多孔耐火砖导热系数受辐射传热的影响明显, 并给出了模型的具体表达式。Gong等[ 26, 27]利用淀粉固结发泡法制备了孔隙率在72%~86%之间的多孔莫来石, 并采用瞬态平板热源法(TPS)测量其导热系数。认为该材料是由致密莫来石骨架和空气组成的两相系统, 通过比较实测值及理论模型计算值, 得出其热导率介于Maxwell-Eucken1和EMT模型之间, 并建立了热导率与孔隙率依赖关系的简单模型。综上所述, 尽管各种模型均作了多种假设, 但因实际多孔材料结构复杂且具独特性, 正如Carson等[ 28]采用二维有限元分析了稳态导热模型后认为的那样, 试图以唯一模型评价所有多孔材料导热系数的做法不切实际。
本研究以高铝矾土、硅灰作原料, 玉米淀粉作造孔剂制备多孔莫来石, 并进行结构表征及性能测试。在抗折强度、体积密度、导热系数与气孔率等关系基础上, 综合考虑气孔率、平均孔径、热辐射及温度等因素对导热系数的影响, 建立了高精度的非线性导热模型。
以高铝矾土(山西阳泉产)和硅灰(市售)为原料, 按Al2O3/SiO2=3:2 (摩尔比)计算并称重所需铝矾土及硅灰。造孔剂为玉米淀粉(市售), 粘结剂为1wt%羧甲基纤维素(CMC)水溶液。原料经200目过筛, 与不同淀粉添加量0wt%~35wt%混合, 以250 r/m转速球磨1.0 h, 球磨介质为去离子水。球磨料经烘干、分散后添加8wt%的CMC溶液, 经造粒、陈腐、模具干压成型, 尺寸为 ϕ185 mm×10 mm, 成型压力为48.23 MPa, 保压4 min制得生坯, 生坯经105℃× 12 h干燥, 分别在1150 ~1500℃温度下煅烧1 h制得样品。
采用X射线衍射仪(Bruker AXS D8-Focus)对样品进行物相分析, 扫描范围10°~70°, CuKa靶, Ni滤波, 管电压40 kV, 管电流40 mA。采用场发射扫描电子显微镜(SU8010, 日本Hitachi公司)观察样品形貌。采用阿基米德法测定样品体积密度和显气孔率。采用三点弯曲法测试样品的抗折强度, 每组5块, 尺寸120 mm×20 mm×10 mm, 加荷速率1 mm/min。采用压汞法(Micromeritics AutoPore IV 9510型) 测定样品孔径分布, 采用PBD-02型平板导热仪测试样品导热系数。
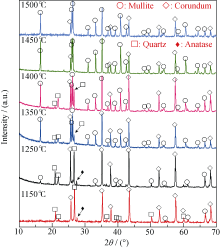
图1为不同温度下煅烧产物XRD图谱。1150℃煅烧产物仍以石英相(PDF No. 78-1253)、刚玉相(PDF No. 71-1123)为主, 仅生成少量莫来石相(PDF No. 79-1276), 锐钛矿相(PDF No. 76-1939)存在因高铝矾土原料含少量杂质所致。1150~1450℃时, 方石英的特征峰先增强后下降直至消失, 而莫来石相衍射峰逐渐增强。1450~1500℃时, 产物以莫来石为主晶相, 同时存在少量刚玉相。
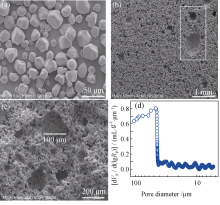
图2为淀粉原料及淀粉含量为25wt%的样品1500℃煅烧1 h产物SEM照片。由图2(a)可知, 成孔剂玉米淀粉的粒径分布在5~20 μm, 形状为近似球形。由图2(b)可见, 产物为贯通多孔结构, 气孔孔径均匀, 白色方框内大孔为淀粉大颗粒燃尽留下。由图2(c), 气孔孔径分布在10~100 μm之间, 孔形貌基本保持了淀粉颗粒近似球形的形貌特征。图2(d)为压汞法所测多孔莫来石的孔径与压入汞体积累积的关系。由图2(d), 多孔莫来石的孔径范围为5.40~105.12 μm, 按体积法计算孔径中值, 并用中间插值法求得平均孔径为46.38 μm。
图3是淀粉添加量对煅烧产物体积密度、显气孔率、抗折强度的影响。样品的体积密度和抗折强度均随淀粉含量的增加而降低, 而显气孔率则随淀粉含量增加而增加。0wt%淀粉含量样品体积密度为1.57 g/cm3, 显气孔率为51.03%, 抗折强度为49.31 MPa, 这缘于实验中采用硅灰作为原料。硅灰不仅具有高反应活性, 可与铝矾土中Al2O3反应生成莫来石, 而且具有球形中空结构, 同时也起到造孔的作用; 含50wt%淀粉的样品体积密度低至1.02 g/cm3, 显气孔率高达73.22%, 抗折强度为3.36 MPa。
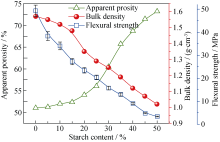 | 图3 淀粉含量对显气孔率、体积密度和抗折强度的影响Fig. 3 Influence of starch content on the apparent porosity, bulk density and flexural strength |
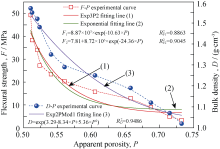
图4是气孔率 P与抗折强度 F、体积密度 D的关系及指数拟合曲线。抗折强度 F和体积密度 D均随气孔率 P的增大而减小。抗折强度 F与气孔率 P之间按2种函数关系拟合, 分别得 F1= f( P)、 F2= f( P)函数关系式, 见式(1)~(2)。体积密度 D与气孔率 P之间拟合方程见式(3)。其中式(1)与Magdeski等[ 29]提出的抗折强度 F与气孔率 P关系模型类似。显然, 式(2)相关系数更高, 可更准确地反应 F= f( P)函数关系。
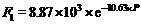 | (1) |
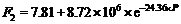 | (2) |
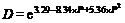 | (3) |
多孔陶瓷由陶瓷骨架(固相)和孔洞内空气(气相)组成, 常温(~298 K)其导热系数 λf与气孔率 P之间最常见五种经典模型[ 16, 17, 18, 19, 20]为Parallel Model (式(4))、Series Model (式(5))、Maxwell-Eucken1 (式(6))、Maxwell-Eucken2 (式(7)) 及Effective Media Theory Model (式(8))。
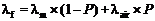 | (4) |
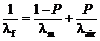 | (5) |
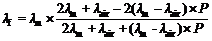 | (6) |
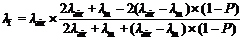 | (7) |
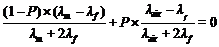 | (8) |
式(4)~(8)中, λf为多孔材料导热系数; λm为零气孔率致密材料导热系数; λair为空气导热系数; P为多孔材料显气孔率;对于多孔莫来石而言, T=298 K, 0≤ P≤1, λair(298 K) ≈ 0.026 W/(m·K), λm(298 K) ≈ 6.0 W/(m·K), 分别代入式(4)~(8)中, 计算结果见图5所示。图中实心圆点()为 T=298 K实测值与气孔率 P对应关系曲线, 这些点恰好落在Maxwell-Eucken2曲线上, 说明实验所制多孔莫来石导热系数 λf与气孔率 P的关系可较好地符合Maxwell-Eucken2 (ME2)模型, 即存在1连续相(固相)及1分散相(气相)。
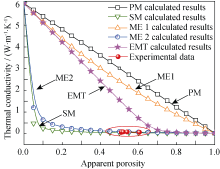 | 图5 五种模型对应导热系数与气孔率关系计算值及实测值Fig. 5 Calculated values of the relationships between thermal conductivity and porosity by five basic models and the experimental values at 298 K |
但是, 与常温298 K多孔材料的导热系数 λf与气孔率 P之间最常见的五种经典模型相比, 多孔材料在高于常温条件服役时导热系数 λf与气孔率 P之间的关系应除考虑固相热传导、气相热传导以外, 还应考虑其高温热辐射效应, 故高于常温条件下的导热模型必定要较常温条件下的导热模型复杂许多。Shimizu等[ 25]根据Ashby-Glicksman Model[ 25]和Kunii Model[ 30], 并考虑高温辐射传热影响, 提出高气孔率高铝耐火材料导热系数 λf与气孔率 P、温度 T及气孔平均孔径 φp之间的关系式, 见式(9)所示。
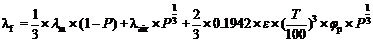 | (9) |
式中, ε为热辐射系数; 这里, 高于常温298 K时, 以Shimizu Model为依据, 即采用式(9)对实验所得不同显气孔率的多孔莫来石在673~1473 K温度范围计算其导热系数。其中, ε = 0.85[ 31], 平均孔径 φp=46.38 μm, λm、 λair数值见表1所示, 计算结果及实测值见图6所示。由图6可知, 根据Shimizu Model导热模型, 即式(9)计算所得的导热系数 λf与温度 T关系曲线与实测导热系数 λf与温度 T关系相差较大, 说明Shimizu Model导热模型仍难以解释实验所得多孔莫来石导热系数 λf与温度 T、平均孔径 φp等之间关系。
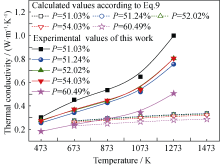 | 图6 Shimizu Model导热系数计算值与实测值比较Fig. 6 Contrast of the calculated values according to Shimizu model and experimental values of this work |
| 表1 零孔隙率莫来石[ 32]及空气导热系数[ 25] Table 1 Typical values of the thermal conductivity for bulk mullite and air at different temperature |
因此, 为更准确地解释实验所得多孔莫来石的孔结构、气孔率 P、温度 T与导热系数 λf之间的关系, 对Shimizu Model即式(9)进行了修订, 经一系列推导, 得到衡量多孔莫来石材料孔结构、气孔率 P、温度 T与导热系数 λf关系的新模型(推导过程详见附件1), 新模型见式(10)所示。
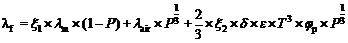 | (10) |
其中, δ为斯忒藩-玻尔兹曼(Stefan-Boltzmann)常数, δ=5.67×10-8W/(m2·K4); ξ1、 ξ2均是与气孔率 P有关的参数, ξ1、 ξ2表达形式相同, 不同之处在于 ξ1、 ξ2中 α1~ α5参数不同, ξ1、 ξ2表达形式见式(11)所示, ξ1、 ξ2式中对应 α1~ α5参数见表2所示;
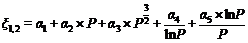 | (11) |
为验证新导热模型准确性, 根据实验所得多孔莫来石的不同显气孔率, 分别于473~1773 K温度范围计算其导热系数 λf与温度 T的关系曲线, 并与多孔莫来石于473~1273 K温度范围实测值进行对比, 结果见图7所示。由图7可知, 据新导热模型式(10)计算结果与多孔莫来石在473~1273 K温度范围导热系数实测值吻合较好, 新导热模型式(10)能够很好地解释实验数据。同时说明推导所得新导热模型式(10)能够准确反映实验所制多孔莫来石导热系数 λf与温度 T、气孔率 P及气孔平均孔径 φp之间的关系。
| 表2 ξ1、 ξ2数学表达式中α1~α5参数值 Table 2 Parameter values of α1- α5 |
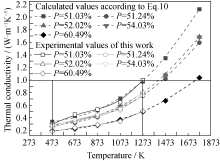 | 图7 新模型导热系数计算数值与实测值比较Fig. 7 The contrast of the calculated values according to the new thermal conductivity model Eq.10 and experimental values |
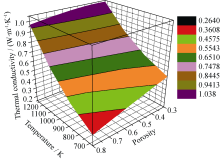
图8为根据新模型式(10)计算的气孔率区间为30%~80%的多孔莫来石在673~1273 K温度范围内的导热系数值。由图8可知, 温度相同, 随气孔率 P增加, 导热系数 λf降低且高温较低温降低幅度变小。673 K时, 气孔率 P由30%增加到80%, 导热系数 λf由0.4919 W/(m·K)降低至0.2655 W/(m·K), 降低46.03%。而1273 K时, 气孔率 P由30%增加到80%, 导热系数 λf由1.0349 W/(m·K)降低至0.9668 W/(m·K), 仅降低6.58%; 对相同气孔率 P, 随温度 T升高, 导热系数 λf增大, 且高气孔率较低气孔率致导热系数 λf增大幅度变大。 气孔率 P=30%时, 温度由673 K升高至1273 K, 导热系数 λf由0.4919 W/(m·K)增大至1.0349 W/(m·K), 增大110.39%。气孔率 P=80%时, 温度由673 K升高至1273 K, 导热系数 λf由0.2655 W/(m·K)增大至0.9668 W/(m·K), 增大264.14%。说明高温下辐射对多孔材料导热系数有重要影响。图8所示结果符合多孔材料导热系数随气孔率 P、温度 T等因素变化的一般规律。同时, 通过模型计算的多孔莫来石导热系数与文献[23,26]实测的多孔莫来石的导热系数基本一致。说明根据实验结果建立的新的非线性导热模型具有较高的准确性。
1) 以铝矾土及硅灰为原料, 0wt%淀粉添加量煅烧样体积密度1.57 g/cm3, 显气孔率51.03%, 抗折强度达49.31 MPa;
2) 高气孔率莫来石的体积密度 D、抗折强度 F随气孔率 P增加而减小, 且符合指数函数关系;
3) 常温时, 多孔莫来石导热系数 λf较好地符合Maxwell-Eucken2模型; 高于常温时, 多孔莫来石的导热系数 λf与Shimizu Model相差较大;
4) 建立了高于常温时可准确反映多孔莫来石导热系数 λf与温度 T、气孔率 P、平均孔径 φp、热辐射之间关系的非线性导热模型: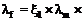
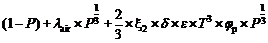 。
。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|