王晓媛(1984-), 女, 助理研究员. E-mail:401wangxy@caep.cn
利用基于密度泛函理论的第一性原理的方法研究了超薄钛酸铅(PbTiO3)纳米管的铁电性及力电耦合特性。研究发现对于钛酸铅铁电纳米管结构, 即使在其特征尺寸小于铁电薄膜的铁电临界尺寸时, 依然存在自发极化。钛酸铅铁电纳米管结构不存在铁电临界尺寸。对纳米管力电耦合效应的研究发现, 轴向应变作用会引起包括极化沿轴向方向的铁电相、顺电相和极化沿周向方向的铁电相在内的丰富的相转变。这种相的转变是由于轴向应力所导致的Pb-O共价键的变化所引起的。另一方面, 研究了钛酸铅纳米管结构的机械强度, 明确了在轴向拉伸和压缩作用下纳米管的临界载荷。
Ferroelectric properties and its coupling behavior with mechanical strain of ultrathin PbTiO3 nanotubes were investigated by first-principles calculations. The spontaneous polarization still exists in the nanotube despite their sidewalls thinner than the critical thickness at which the thin films lose ferroelectricity, which indicates the absence of an intrinsic critical size of ferroelectricity. Moreover, the total energy of nanotube is lower than that of the thin film. This means that the nanotube structure is energetically more stable than the thin film. In addition, the coupling behavior of ferroelectricity and axial strain is also studied. The axial polarization of nanotube is enhanced by the tensile strain. On the other hand, with the increase of compressive strain, the axial polarization becomes weak and disappears, and the nanotube structure becomes paraelectric state. With the further increase of compressive strain, a vortex type of polarization emerges along the circumferential direction, and the nanotube structure becomes ferroelectric state again. These rich phase transitions in the nanotube structure are induced by the change of covalent Pb-O bond due to the applied strain. Finally, the mechanical strength of PbTiO3 nanotube is evaluated, and the critical stresses under the tension and compression states are obtained.
铁电纳米管作为一维多功能材料得到广泛应用, 例如应用于铁电随机存储器及一些微纳米电子器件等[ 1]。铁电纳米管的电学性质与管壁的厚度密切相关[ 2], 深入研究铁电纳米管的铁电性具有重要意义。近年来, 随着纳米加工技术的发展和电子元器件小型化、集成化的需求, 实验室已成功制备纳米级管壁厚的铁电纳米管[ 3]。在特征尺寸如此小的铁电纳米管中, 其铁电性的变化引起了人们浓厚的兴趣。铁电材料的铁电性来源于长程库仑力和短程分子间范德华力之间的相互作用及其平衡[ 4], 低维纳米材料的结构及尺寸都会影响该平衡作用, 从而影响材料的铁电性。另外, 在铁电材料的表面附近, 垂直于结构表面方向的铁电极化会引起表面电荷的聚集, 导致表面产生退极化场。由于该退极化场的电场方向与自发极化的方向相反, 会引起表面附近极化的不稳定性, 甚至会导致铁电极化的消失。因此人们预测, 在纳米尺度下, 随着材料特征尺寸的进一步减小, 表面对材料铁电性的影响会进一步增强, 由表面电荷聚集所产生的退极化场对铁电极化的抑制作用可能会导致铁电材料在某个特征尺寸下发生铁电-顺电相变。这一特征尺寸被称为铁电临界尺寸[ 5, 6]。
近年来, 人们已经从理论和实验两方面研究了纳米铁电材料, 尤其是纳米铁电薄膜的铁电临界尺寸。例如, 生长在钛酸锶基体上的极薄钛酸铅铁电薄膜, 其铁电临界尺寸为0.8 nm[ 7]; 生长于不同基体上的钛酸钡铁电薄膜的铁电临界尺寸在2~10 nm范围[ 8, 9, 10]。然而, 关于铁电纳米管有无铁电临界尺寸及其大小, 迄今无人研究。
纳米管由于其结构特点, 内壁会受到结构所产生的压应力。以往的研究证明, 铁电材料尤其是纳米铁电材料有着强烈的力电耦合作用, 应力和应变会严重影响其铁电稳定性[ 11]。因此, 本研究还将研究轴向应变对纳米管结构铁电性的影响。另一方面, 由于纳米管结构在工作环境中经常会受到轴向载荷的作用, 为保证结构的可靠性, 有必要进一步明确纳米管结构的拉伸和压缩强度。
本工作主要研究铁电纳米管结构的铁电稳定性, 研究在极薄的铁电纳米管中(壁厚小于铁电临界尺寸下铁电薄膜的厚度)是否存在铁电临界尺寸及其大小。并研究纳米管的力电耦合效应及其机械强度。选取钛酸铅(PbTiO3)铁电材料, 它是典型的钙钛矿型铁电体。利用基于密度泛函理论的第一性原理的方法, 从原子和电子的角度深入研究极薄纳米管的铁电临界尺寸、微观极化分布以及应变场对纳米管结构铁电性及力电耦合特性的影响。
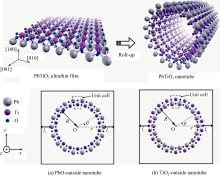
第一性原理计算所采用的软件包为VASP软件包, 计算中所采取的交换关联势为局域密度近似, 所选取的平面波截断能为500 eV。为了准确描述原子核与电子之间的相互作用, 本计算中的价电子包含Pb5d、6s、6p; Ti3s、3p、3d、4s和O2s和2p。所选参数的准确性已在以往计算中得到验证[ 12, 13]。钛酸铅纳米管的计算模型如图1所示, 其中纳米管的壁厚为一个晶格厚度, 该厚度小于钛酸铅铁电薄膜的铁电临界尺寸[ 7]。纳米管结构可以看作是由一个(100)超薄薄膜沿[001]方向绕转而成, 模型的轴向、周向和径向方向分别为[001]、[010]和[100]向。对于壁厚为一个晶格厚度的钛酸铅纳米管, 其原子结构有两种排布方式, 即(1)外侧由PbO层, 内侧由TiO2层组成; (2)外侧由TiO2层, 内侧由PbO层组成。这两种结构分别表示在图1(a)和(b)中。纳米管的半径 R取决于沿周向方向组成结构的晶格数目 N的大小。为了获得稳定的纳米管结构, 本文研究了不同半径的铁电纳米管( N=10~22)。第一性原理计算模型需满足周期性边界条件, 因此为了避免相邻纳米管之间的相互作用, 分别在[100]和[010]方向引入 lv=2 nm厚的真空层, 该厚度的合理性已在预计算中进行了验证。计算中, 布里渊区积分时所采取的 k点网格选为1×1×6网格。
为了研究纳米管结构的稳定性, 首先计算了纳米管的内聚能( Ec), 定义为:
 | (1) |
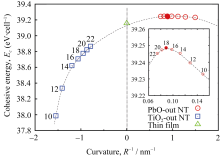
其中, EPb、 ETi和 EO分别表示独立的Pb、Ti和O原子的能量, Etube表示纳米管的总能量。图2描述了纳米管内聚能 Ec与曲率1/ R之间的关系, 其中半径 R取管的内径 Rin和外径 Rout的平均值。对于所有的纳米管结构, 内聚能均为正值, 意味着纳米管结构为稳定结构[ 14]。同时, 外侧为PbO层的纳米管结构的内聚能大于相同厚度的薄膜结构的内聚能, 进一步证实了纳米管结构的稳定性。而外侧为TiO2层的纳米管结构的内聚能则小于薄膜结构的内聚能。对于PbO外侧的纳米管结构, 当 N=18时, 内聚能最大( Ec =39.25 eV/cell), 结构最为稳定, 此时纳米管的内外径分别为 Rin=1.017 nm和 Rout= 1.189 nm。事实上, 在氧化物和金属纳米管中也发现了管状结构比薄膜结构更为稳定的现象, 例如TiO2纳米管[ 15]和Au纳米管[ 16]。
为了研究铁电纳米管的铁电性, 引入矢量 P来表征自发极化的大小, 即:
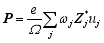 | (2) |
其中, Ω、 e和 uj分别表示单位元胞的体积、单位电荷和第 j个原子相对于理想晶格结构的位移, Z*j为第 j个原子的波恩有效电荷[ 17]。 ωj为共享第 j个原子的元胞数的倒数。这种定义已被广泛用来讨论纳米铁电材料的极化大小[ 18, 19, 20]。
对PbO外侧 N=18的钛酸铅纳米管铁电性的研究发现, 沿[001]方向, 纳米管结构存在自发极化, 大小为 Pz=5.12 µC/cm2(块体材料的自发极化大小为 Pz=78.6 µC/cm2)。而对于相同厚度的薄膜结构, 其稳定相为顺电相, 无自发极化。因此, 不同于钛酸铅纳米薄膜结构[ 7], 钛酸铅纳米管无铁电临界尺寸。
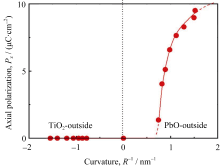
对于不同半径的纳米管结构, 我们还分别研究了轴向极化 Pz与曲率1/ R之间的关系, 如图3所示。对于PbO外侧的纳米管结构, 极化随曲率的增加而增加; 而对于TiO2外侧的纳米管结构, 铁电极化的大小为零, 结构呈顺电相。这是因为由于纳米管自身的结构特点, 其内侧受到弯曲变形, 会在管内壁引起均匀的压应力。在外侧为PbO层, 内侧为TiO2层的纳米管结构中, 内侧的TiO2内层会产生明显的褶皱现象, 从而驰豫内部压缩应力的影响, 降低应变能, 使结构的自由能降低, 加强其稳定性。事实上, 在TiO2极薄纳米管中也发现了由TiO2层的受压屈曲产生褶皱提高系统结构稳定的现象[ 13]。
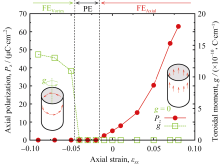
为了系统研究轴向应变对纳米管铁电性的影响, 我们以PbO外侧 N=18的纳米管为例, 沿[001]方向分别对系统施加拉伸和压缩应变。图4表示PbO外侧纳米管中铁电极化随拉伸和压缩应变的变化曲线。可以看到, 随着拉伸应变的增大, 铁电极化平稳增加。这是因为拉伸应变增加了结构的四方性。另外, 在受压情况下, 当压应变 εzz= -0.02时自发极化消失, 结构由铁电相转变为顺电相。而当压应变进一步增大到 εzz = -0.05时, 将重新出现铁电极化。然而, 此时的极化并非沿轴向方向, 而是沿纳米管周向方向的涡旋状极化。我们引入偶极矩 g来评价周向方向涡旋极化的大小, 定义为:
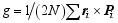 | (3) |
其中, ri和 Pi分别表示沿周向方向第 i个晶胞距离纳米管中心位置的位移矢量和局部极化矢量。从图4中可以看到, 偶极矩 g随压应变的增大而增加。因此, 在轴向应变的作用下, 纳米管将体现出包括极化沿轴向方向的铁电相、顺电相和极化沿周向方向的铁电相在内的丰富的铁电相变。
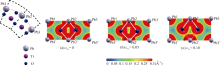
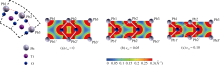
由于理论[ 21]和实验[ 22]研究均验证了钛酸铅铁电材料的强铁电性和铁电稳定性来源于Pb-O共价键的作用, 这种共价键作用是Pb 6s和O 2p轨道杂化的结果。因此我们通过研究Pb-O共价键的强弱来解释纳米管中应力所导致的铁电相变。图5和图6分别显示了在不同轴向拉伸应力和压缩应力作用下PbO外侧 N=18纳米管结构中PbO层的电荷密度分布图, 其中白色实线表示Pb-O共价键。在应力为零的状态下, α键的共价键强度略大于 β键( α共价键之间的最小电荷密度为4.644×103 nm-3, β共价键之间的最小电荷密度为4.633×103 nm-3), 纳米管结构的铁电性较小。从图5中可以看到, 随着拉伸应力的增大, α键进一步增强而 β键逐渐减弱。由于PbTiO3铁电材料的强铁电性来源于Pb-O共价键的作用, 因此, α键的增强和 β键的削弱导致了沿轴向方向铁电极化 Pz的稳步增加。另一方面, 随着轴向压应力的进一步增大, 当 εzz= -0.05时, α键及 β键断开, 同时Pb2与O1形成新的 γ及 γ′键。此时 α′( β′)键与 γ( γ′)键键长相等, 方向均指向纳米管周向方向, 从而导致沿周向方向出现铁电极化。此时, 纳米管的稳态结构为铁电极化沿纳米管周向方向的铁电态结构。随着轴向压应力的继续增加, α′( β′)键与 γ( γ′)键进一步显著增强, 从而导致沿周向方向铁电极化的增大。总而言之, 轴向拉应力导致沿轴向方向四方相结构的增强, 从而导致轴向方向Pb-O共价键的增强, 继而导致轴向方向铁电性的增强;轴向压缩应力则导致沿纳米管周向方向四方向结构和Pb-O共价键作用的增强, 继而导致沿周向方向出现铁电极化。因此, 轴向应力的作用导致Pb-O共价键的改变, 从而导致了丰富的铁电相变。
本节着重探讨铁电纳米管的拉伸及压缩强度, 首先研究钛酸铅纳米管的应力-应变关系。图7为外侧PbO层, N=18的超薄钛酸铅纳米管分别在轴向拉伸和压缩应变 εzz作用下轴向应力 σzz的变化曲线。在拉伸及压缩过程中, 纳米管结构在垂直于拉伸方向上为完全松弛优化, 模拟过程为考虑了泊松效应的单轴拉伸/压缩过程。
在轴向拉伸时, 轴向应力 σzz随拉伸应变 εzz的增加而单调增大, 并在应变 εzz=0.06时轴向应力达到最大值, 即 σzz=7.06 GPa。因此, 钛酸铅纳米管的拉伸强度为7.09 GPa。在轴向压缩时, 轴向应力 σzz随压缩应变 εzz的增加而逐渐增大, 在 εzz=-0.04时轴向应力达到最大值 σzz= -8.60 GPa。所以, 钛酸铅纳米管的压缩强度为-8.60 GPa。表1给出了纳米管结构在轴向拉伸和压缩时临界应力和断裂应变的具体数值。将钛酸铅纳米管内外壁的半径差定义为 l0, 故而将纳米管看作厚度为2 l0的管柱状结构。纳米管的弹性模量由应力—应变曲线 εzz=0处的斜率确定。因此, 应力为零时钛酸铅纳米管的弹性模量为206 GPa。同时, 在纳米管的拉伸和压缩过程中, 应力-应变曲线的斜率基本保持不变, 即弹性模量的值变化不大(在±3%的范围内)。
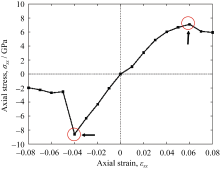 | 图7 PbTiO3纳米管中轴向应力 σzz随轴向应变 εzz的变化曲线Fig. 7 Relation between the axial stress ( σzz) and the axial strain ( εzz) in PbTiO3 nanotube |
值得注意的是, 本研究获得的纳米管的机械强度是纳米管结构的理论强度, 即假设纳米管在受拉时发生理想均匀变形, 结构发生弹性失稳时所能承受的最大应力值。理论强度是实际纳米管材料的强度上限值。而对于实际纳米管材料, 由于内部缺陷等多种因素的影响, 材料的强度会大大降低。通过第一性原理计算其理论强度对了解纳米管结构的力学性能是非常必要的。
| 表1 PbTiO3纳米管在拉伸和压缩状态下的临界应力和断裂应变 Table1 Critical stress and fracture strain of PbTiO3 nanotube in tension and compression |
利用基于密度泛函理论的第一性原理方法研究了超薄钛酸铅纳米管的铁电性, 力电耦合特性和强度特性。研究发现, 即使在壁厚仅有一个晶胞厚度的钛酸铅纳米管中, 依然存在铁电极化。意味着钛酸铅纳米管结构无铁电临界尺寸。另一方面, 在轴向应变的作用下, 纳米管结构呈现出丰富的相的转变, 这是由于应变导致Pb-O共价键的变化所引起的。关于纳米管的机械强度的研究则发现, 钛酸铅纳米管的拉伸和压缩强度分别为7.09 GPa和-8.06 GPa。本研究可为纳米铁电材料的进一步小型化应用及结构的优化设计提供理论依据。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|